Основные понятия кинематики

Самостоятельная работа

V. Итог урока

Состав какого числа мы сегодня выучили? Повторим его еще выполнив» домик № 9.

Запомни!!!

Вариант 1 9 = 6 + __ 8 = 6 + __ 8 = 1+ __ 9= 8 + __ 9 = 7+ __ 8= 5 + __ 8 = 3 + __ 9 = 1 + __ 8 = 2 + __ 9 = 3 + __ 8 = 4 + __ 8 = 7+ __ 9 = 2 + __ 9 = 5 + __

Вариант 2 8 = 2 + __ 9 = 3 + __ 8 = 4 + __ 8 = 7+ __ 9 = 2 + __ 9 = 5 + __ 9 = 6 + __ 8 = 6 + __ 8 = 1+ __ 9= 8 + __ 9 = 7+ __ 8= 5 + __ 8 = 3 + __ 9 = 1 + __

· Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.

· Система отсчёта — сопоставленная с континуумом реальных или воображаемых тел отсчёта система координат и прибор (ы) для измерения времени (часы). Используется для описания движения.

· Координаты — способ определения положения точки или тела с помощью чисел или других символов.

· Радиус-вектор используется для задания положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

· Траектория — непрерывная линия, которую описывает точка при своём движении.

· Скорость — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.

· Ускорение — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени.

· Угловая скорость — векторная величина, характеризующая скорость вращения тела.

· Угловое ускорение — величина, характеризующая быстроту изменения угловой скорости.

Материальная точка — объект, размерами которого в условиях данной задачи можно пренебречь, считая его массу сосредоточенной в одной точке пространства. Материальная точка – это тело, размерами которого в данных условиях можно пренебречь. Система отсчета – это тело отсчета, связанная с ней система координат и прибор для фиксации момента времени, в который мы рассматриваем положение тела – часы. Ра́диус-ве́ктор (обычно обозначается или просто 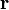) — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки, называемой началом координат.

Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку. Вектор перемещение — это вектор, соединяющий начальное и конечное положение материальной точки в пространстве. Направленный отрезок прямой, соединяющий два последовательных положения тела (либо его начальное и конечное положения), называется перемещением. Линия, вдоль которой движется тело, называется траекторией. Траектория — линия в пространстве, вдоль которой движется материальная точка.Длина траектории называется путем. Путь обозначают буквой L.

Путь - величина скалярная. Путь — это длина траектории.

3. Ско́рость (часто обозначается 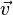, от англ. velocity или фр. vitesse) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени. Этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, т. е. проекцию этого вектора на касательную к траектории точки. Сре́дняя ско́рость — в кинематике, некоторая усреднённая характеристика скорости движущегося тела (или материальной точки). Различают два основных определения средней скорости, соответствующие рассмотрению скорости как скалярной либовекторной величины: средняя путевая скорость (скалярная величина) и средняя скорость по перемещению (векторная величина). При отсутствии дополнительных уточнений, под средней скоростью обычно понимают среднюю путевую скорость. Средняя (путевая) скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:

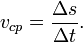Мгновенная скорость — векторная физическая величина, равная первой производной от радиус-вектора по времени:

.

4. Ускорением называют физическую величину, характеризующую быстроту изменения мгновенной скорости тела. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, называется ускорение. Средним ускорением неравномерного движения в интервале от t до t+Δt называется векторная величина, равная отношению изменения скорости Δ v к интервалу времени Δt:

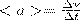
Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет векторная величина:

равная первой производной скорости по времени. Тангенциальная составляющая ускорения:

т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
Ищем вторую составляющую ускорения. Допускаем, что точка В сильно близка к точке А, поэтому Δs можно считать дугой окружности некоторого радиуса r, слабо отличающейся от хорды АВ. Треугольников АОВ подобен треугольнику EAD, из чего следует Δv_n/AB=v₁/r, но так как AB=vΔt, то

В пределе при Δt→0 получим v₁→v. Т.к. v₁ → v, угол EAD стремится к нулю, а т.к. треугольник EAD равнобедренный, то угол ADE между v и Δ v_n стремится к прямому. Следовательно, при Δt→0 векторы Δ v_n и v становятся взаимно перпендикулярными. Т.к. вектор скорости направлен по касательной к траектории, то вектор Δ v_n, перпендикулярный вектору скорости, направлен к центру кривизны траектории точки. Вторая составляющая ускорения, равная

называется нормальной составляющей ускорения и направлена по прямой перпендикулярной касательной к траектории (называемой нормалью) к центру ее кривизны (поэтому ее называют также центростремительным ускорением). Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих:

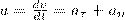
Значит тангенциальная составляющая ускорения является характеристикой быстроты изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения — характеристикой быстроты изменения скорости по направлению (направлена к центру кривизны траектории). В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
1)a_τ=0, a_n=0 — прямолинейное равномерное движение;
2)a_τ=a_n=const, а_n=0 - прямолинейное равнопеременное движение. При таком виде движения

Если начальный момент времени t₁ = 0, а начальная скорость v₁ = v₀, то, обозначив t₂=t и v₂ = v, получим a =(v - v₀)/t, откуда

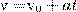
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

3)a_τ=f(t), a_n=0 — прямолинейное движение с переменным ускорением;
4)a_τ=0, a_n=const. При a_τ=0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы a_n=v²/r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным;равномерное криволинейное движение;
5)a_τ=0, a_n≠0 равномерное криволинейное движение;
6)a_τ=const, a_n≠0 - криволинейное равнопеременное движение;
7)a_τ=f(t), a_n≠0 - криволинейное движение с переменным ускорением.

5. Враща́тельное движе́ние — вид механического движения. При вращательном движении материальной точки она описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна. Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
. Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
термин угловое перемещение не применим к вращательной форме движения. Вращающееся тело с неподвижной относительно системы координат осью вращения не перемещается в этой системе координат. Угловое перемещение относится лишь к центру масс тела, движущегося по криволинейной орбите, его надо понимать, как приращение угла поворота d φ _orb радиуса кривизны траектории R.

Само же орбитальное перемещение − это элементарный путь d s, пройденный телом по криволинейной траектории, и он равен

d s = R d φ _orb. (1) Обратим еще раз внимание на то, что угол поворота d φ _rot и угловое перемещение d φ _orb являются разными величинами, хоть и имеют одну природу. Угол поворота относится только к вращению тела, а угловое перемещение относится к орбитальному движению тела, которое при этом может вращаться вокруг собственной оси. И в этом случае d φ _orb ≠ d φ _rot

Дата добавления: 2014-11-08