
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула полной вероятности
|
|
|
|
Вероятность появления только одного события
Пример 4. Пусть даны три независимых события 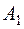 ,
, 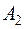 ,
, 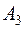 , их вероятности соответственно равны
, их вероятности соответственно равны 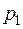 ,
, 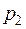 , и
, и 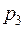 . Найти вероятность появления только одного события.
. Найти вероятность появления только одного события.
¦ Пусть:
событие 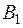 - появилось только событие
- появилось только событие 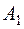 (
(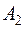 и
и  не появились)
не появились)
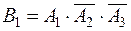
событие  - появилось только событие
- появилось только событие 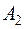 (
( и
и  не появились)
не появились)
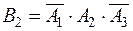
событие 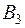 - появилось только событие
- появилось только событие 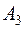 (
( и
и 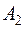 не появились)
не появились)
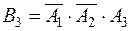
Таким образом, чтобы найти вероятность появления только одного из событий 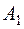 ,
, 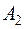 ,
, 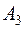 , будем искать вероятность
, будем искать вероятность
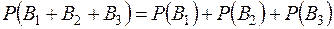 так как события
так как события 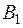 ,
,  ,
, 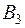 несовместны.
несовместны.
События  ,
, 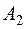 ,
, 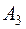 - независимы
- независимы 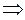
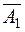 ,
,  ,
, 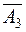 - независимы.
- независимы.
Обозначим 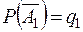 ,
, 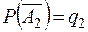 ,
, 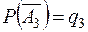 .
.
Тогда 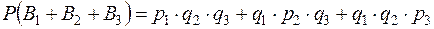 , т.е.
, т.е.
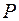 (появления только одного события) =
(появления только одного события) = 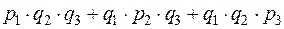 .?
.?
Пусть некоторое событие 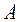 может произойти вместе с одним из несовместных событий
может произойти вместе с одним из несовместных событий 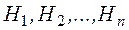 , составляющих полную группу событий. Пусть известны вероятности этих событий
, составляющих полную группу событий. Пусть известны вероятности этих событий 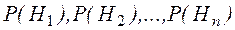 и условные вероятности наступления события
и условные вероятности наступления события 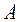 при наступлении события
при наступлении события 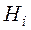 :
:
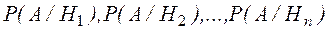 .
.
Теорема. Вероятность события 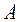 , которое может произойти вместе с одним из событий
, которое может произойти вместе с одним из событий 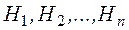 , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события
, равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события 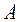 .
.
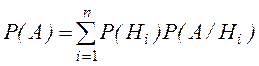
Пример 5. В двух ящиках содержатся по 20 деталей, причем в первом 17 стандартных деталей, а во втором 15 стандартных деталей. Из второго ящика наудачу извлечена одна деталь и переложена в первый ящик. Найти вероятность того, что наудачу извлеченная деталь из первого ящика, окажется стандартной.
¦ Опыт можно разбить на два этапа: первый - перекладывание детали,
второй - выбор детали.
Гипотезы:
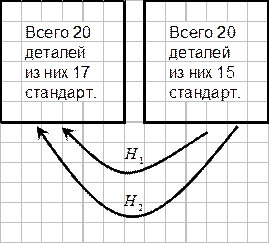
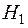 - переложена стандартная деталь;
- переложена стандартная деталь;
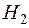 - переложена нестандартная деталь.
- переложена нестандартная деталь.
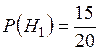 ,
, 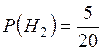 .
.
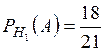 ,
, 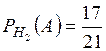 .
.
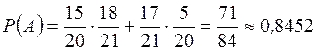 .?
.?
Пример 6. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.
m
Вероятность того, что выстрелы производит первый, второй или третий стрелок равна 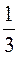 .
.
Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:
- для первого стрелка: 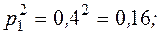
- для второго стрелка: 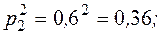
- для третьего стрелка: 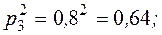
Искомая вероятность равна:
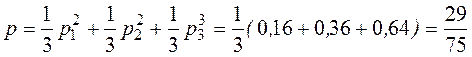 .?
.?
Формула Байеса (формула гипотез)
Пусть имеется полная группа несовместных гипотез 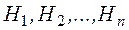 с известными вероятностями их наступления
с известными вероятностями их наступления 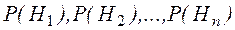 . Пусть в результате опыта наступило событие
. Пусть в результате опыта наступило событие 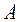 , условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности
, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности 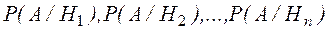 .
.
Требуется определить какие вероятности имеют гипотезы 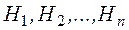 относительно события
относительно события 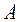 , то есть условные вероятности
, то есть условные вероятности 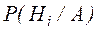 .
.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
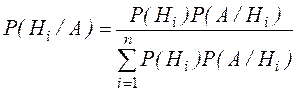
Эта формула называется формулой Байеса.
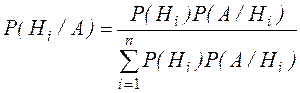 .
.
Пример 7. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру равна 0,6, ко второму равна 0,4. Вероятность того, что деталь будет признана стандартной первым контролером равна 0,94, а вторым – 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что ее проверил первый контролер.
¦ Гипотезы: 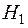 - деталь проверил первый контролер;
- деталь проверил первый контролер;
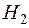 - деталь проверил второй контролер.
- деталь проверил второй контролер.
Событие 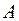 - деталь признана стандартной.
- деталь признана стандартной.
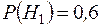
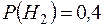
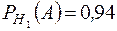
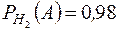

Как видно до испытания 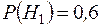 , а после
, а после 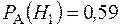 .?
.?
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 1665; Нарушение авторских прав?; Мы поможем в написании вашей работы!