Понятие о фазовой плоскости. Исследование нелинейных систем методом фазовой плоскости

При составлении уравнений динамики нелинейной системы все звенья, поддающиеся линеаризации в преде­лах малых отклонений координат, описываются линейны­ми уравнениями. Для одного или двух (реже — несколь­ких) существенно нелинейных звеньев этой системы составляются нелинейные уравнения (или используются нелинейные характеристики). В общем случае нелиней­ные дифференциальные уравнения динамики в нормаль­ной форме имеют вид

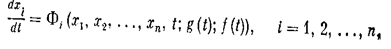
где Хi, (г = 1, 2,..., n ) — координаты состояния системы, g(t), f(t)—соответственно задающие и возмущающие воздействия, или в векторной записи

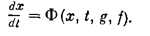
Для рассмотрения переходных процессов, вызванных какими-либо начальными отклонениями координат (при отсутствии внешних воздействий) эти уравнения для систем с постоянными параметрами (т.е. для стационарных систем) принимают вид:

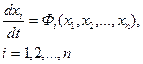(1.1)

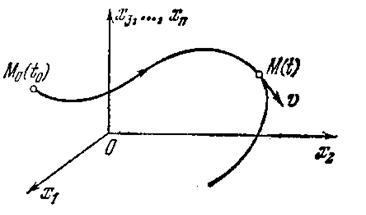
Рис. 1.6.

А в векторной форме:

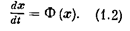
Для исследования нелинейных систем широко исполь­зуется метод фазового пространства, который состоит в следующем. Представим себе n-мерное пространство ко­ординат состояния системы (x1,x2,…xn) (рис 1.6) ^*), называемое фазовым пространством. Тогда начальное со­стояние системы x(to) изобразится определенной точкой М0 с координатами x 1(to) ,x 2(to) ,...,хn (tо), а процесс во времени, т. е. решение уравнений (1.1)

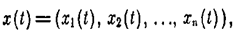
получит изображение в виде некоторой кривой (рис. 1.6),

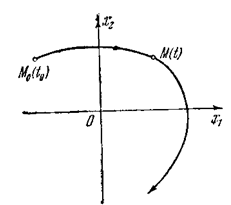
Рис. 1.7.

которая называется фазовой траекторией данной системы. Текущая точка М на ней, соот­ветствующая состоянию систе­мы в произвольный момент вре­мени t, называется изображаю­щей точкой. Отметим, что зна­чения нелинейных функций - 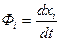, стоящих в уравнениях (1.1) справа, определяют в каждый момент времени проекции, скорости и изображающей точ­ки М на оси координат хi,.

Если в многомерном фазовом пространстве мы лишь мысленно можем представить себе геометрическую карти­ну, то, например, для системы второго порядка (п = 2)

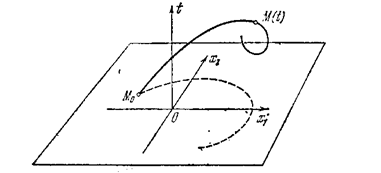
Рис. 1.8.

можно реально изображать фазовые траектории на пло­скости (рис. 1.7). При этом можно изобразить и интег­ральную кривую для данной системы, добавив ось вре­мени t (рис. 1.8).

Уравнения (1.1) при n=2 принимают вид

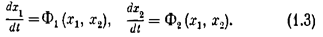
Дифференциальное уравнение фазовой траектории полу­чается путем исключения времени из системы уравне­ний (1.3):

Точки равновесного состояния системы определяются ну­левыми значениями скорости dx 1 /dt =0, dx 2 /dt =0; следовательно,

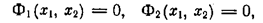
что создает неопределенность правой части уравнения (1.4). Поэтому точки равновесного состояния системы яв­ляются так называемыми особыми точками на фазовой плоскости.

Сопоставим изображение переходного процесса в

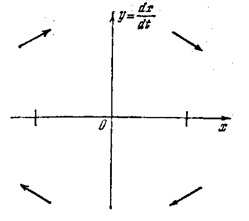
Рис. 1.9.

виде фазовых траектории на плоскости у(х) с обыч­ным его изображением в виде кривой x(t). Для удобства положим, что уравнения (1.3) имеют более простой вид:

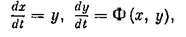
т. е. координата у, откла­дываемая по оси ординат фазовой плоскости, пред­ставляет собой скорость изменения координаты х, откладываемой по оси

абсцисс. В этом случае для изображающей точки спра­ведливо следующее

Правило для направления движения по фазовый тра­екториям:

а) а верхней полуплоскости (рис. 1.9)— слева направо, т.е. в сторону увеличения х, так как там скорость у > 0;

б) в нижней полуплоскости, наоборот,— справа налево;

в) ось х пересекается фазовыми траекториями- под прямым углом, так как там скорость у = 0, т. е. имеет место максимум или минимум величины х.

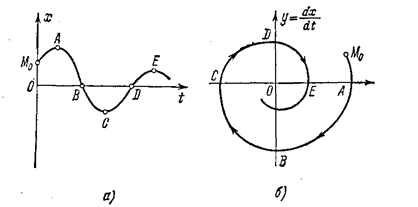
Рис. 1.10.

Заметим, что это правило недействительно в общем случае уравнения (1.3).

Рассмотрим сначала затухающий колебательный про­цесс x(t) (рис.1.10, а). На фазовую плоскость (рис. 1.10, б), где у == dx/dt, нанесем отмеченные на кри­вой переходного процесса точки А, В, С,..., в которых х имеет либо максимум, либо нуль, либо минимум. В ре­зультате получим, что затухающий колебательный про­цесс изображается на фазовой плоскости в виде сходя­щейся спиралевидной кривой.

Аналогично расходящийся колебательный процесс (рис.1.11, а) изобразится па фазовой плоскости в виде расходящейся спиралевидной кривой (рис. 1.11, б).

Очевидно, что периодический процесс (рис. 1.12, а) изобразится на фазовой плоскости в виде замкнутой кри­вой (рис. 1.12, б). За один период колебаний изображаю­щая точка М пробегает весь замкнутый контур, а затем повторяет движение по нему.

Монотонный затухающий процесс x(t) (рис. 1.13, а) изобразится на фазовой плоскости в виде кривой, мо­нотонно приближающейся к положению равновесия

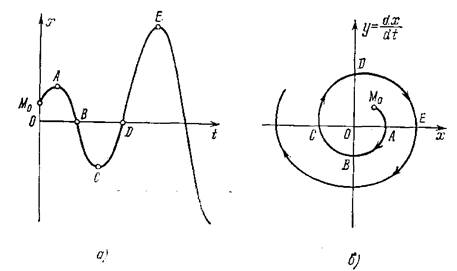
Рис. 1.11.

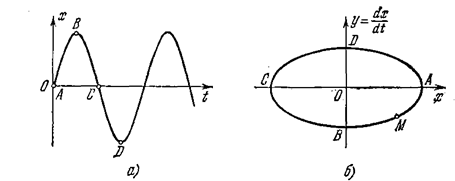
Рис. 1.12.

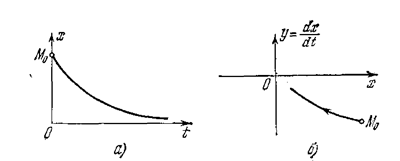
Рис.1.13.

(рис.1.13, б), а монотонный расходящийся процесс (рис. 1.14, а)—в виде монотонно удаляющейся кривой (рис. 1.14, б).

Удобство представления процесса в виде фазовых траекторий на плоскости состоит в том, что вся совокупность

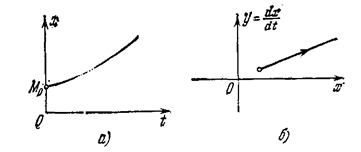
Рис. 1.14.

возможных форм переходных процессов в системе при любых начальных условиях представляется в виде единого «фазового портрета». Недостатком же является то, что мы вынуждены при атом ограничиваться рассмот­рением лишь систем второго порядка. Для исследования нелинейных систем более высокого порядка будут приме­нены другие методы.

Дата добавления: 2014-11-20