Вычисление коэффициентов гармонической линеаризации

Проиллюстрируем вычисление коэффициентов гармонической линеаризации на нескольких примерах: сначала для симметричных колебаний, а затем для несимметричных. Предварительно заметим, что если нечетно-симметричная нелинейность F(x) однозначна, то, согласно (4.11) и (4.10), получаем

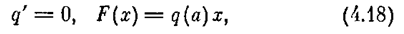
причем при вычислении q (4.11) можно ограничиться интегрированием на четверти периода, учетверив результат, а именно

Для петлевой нелинейности F(x) (нечетно-симметричной) будет иметь место полное выражение (4.10)

причем можно пользоваться формулами

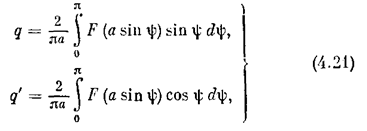
т. е. удвоением результата интегрирования на полупериоде.

Пример 1. Исследуем кубическую нелинейность (рис. 4.4, я):

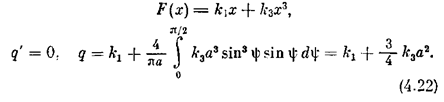
Зависимость q(a) показана на рис. 4.4, б. Из рис. 4.4, а видно, что при заданной амплитуде я прямая q(a)x осредняет криволинейную зависимость F(x) на данном

Рис. 4.4.

участке -а£ х £. а. Естественно, что крутизна q(a) на­клона этой осредняющей прямой q{a}x увеличивается с увеличением амплитуды а (для кубической характе­ристики это увеличение происходит по квадратичному закону).

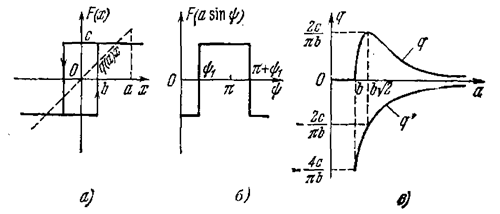
Рис. 4.5.

Пример 2. Исследуем петлевую релейную характе­ристику (рис. 4.5, а). На рис. 4.5,6 представлена подын­тегральная функция F(a sin y) для формул (4.21). Переключение реле имеет место при ½ х ½= b, Поэтому в момент переключения величина y1 определяется выражением sin y1= b /а. По формулам (4.21) получаем (для a ³b)

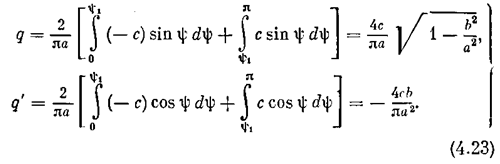
На рис. 4.5, б изображены графики q(а) и q'(a). Первый из них показывает изменение крутизны наклона осредняющей прямой q(а) x с изменением а (см. рис. 4.5, а). Естественно, что q(a)à0 при аॠпри, так как сигнал на выходе остается постоянным (F(x)=c)при любом неограниченном увеличении входного сигна­ла х. Из физических соображений ясно также, почему q' <0. Это коэффициент при производной в формуле (4.20). Положительный знак давал бы опережение сиг­нала на выходе, в то время как гистерезисная петля дает запаздывание. Поэтому естественно, что q' < 0. Абсолют­ное значение q' уменьшается с увеличением амплиту­ды a, так как ясно, что петля будет занимать тем мень­шую часть «рабочего участка» характеристики F(x), чем больше амплитуда колебаний переменной х.

Амплитудно-фазовая характеристика такой нелиней­ности (рис. 4.5, а), согласно (4.13). представляется в виде

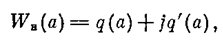
причем амплитуда и фаза первой гармоники на выхода нелинейности имеют соответственно вид

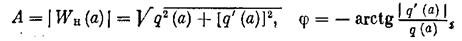
где q и q' определены выше (рис. 4.5, б). Следовательно, гармоническая линеаризация переводит нелинейное ко­ординатное запаздывание (гистерезисную петлю) в экви­валентное запаздывание по фазе, характерное для ли­нейных систем, по с существенным отличием—зависи­мостью фазового сдвига от амплитуды входных колеба­ний, чего нет в линейных системах.

Пример 3. Исследуем однозначные релейные ха­рактеристики (рис. 4.6, а, в). Аналогично предыдущему получаем соответственно

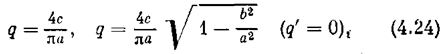
что изображено на рис. 4.6, б, а.

Рис. 4.6.

Пример 4. Исследуем характеристику с зоной нечувствительности, линейным участком и насыщением (рис. 4.7, а). Здесь q' = 0, а коэффициент q (a) имеет два варианта значений в соответствии срис. 4.7, б, где для них построена F (a sin y):

1) при b1 £ а £ b2, согласно (4.19), имеем

что сучетом соотношения a sin y1 = b 1 дает

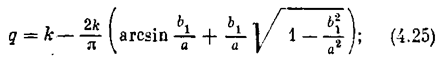
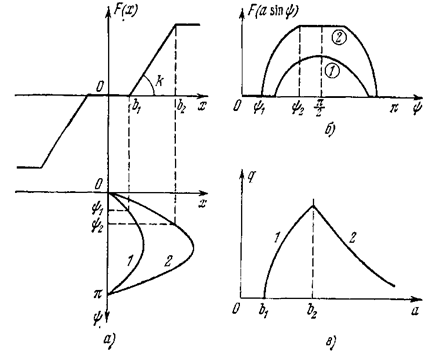
Рис. 4.7.

2) при а ³ b2

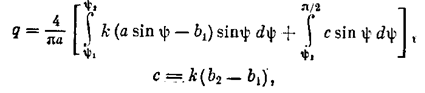
что с учетом соотношения a sin y2 = b2 даёт

Графически результат представлен на рис. 4.7, а.

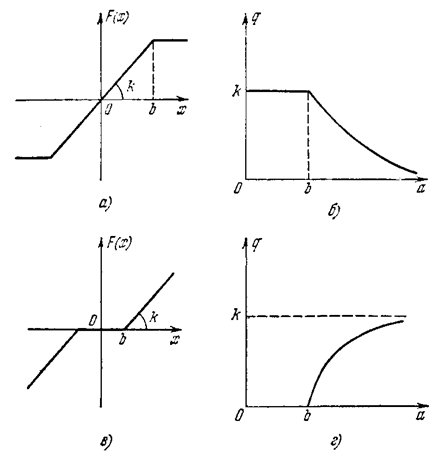
Рис. 4.8.

Пример 5. Как частные случаи, соответствующие коэффициенты q(a) для двух характеристик (рис. 4,8, а, б) равны

что изображено графически на рис. 4.8, б, г. При этом для характеристики с насыщением (рис. 4.8, а) имеем q= k при 0 £ a £ b.

Покажем теперь примеры вычисления коэффициен­тов гармонической линеаризации для несимметричных колебаний при тех же нелинейностях.

Пример 6. Для случая кубической нелинейности F(x) = kx³ по формуле (4.16) имеем

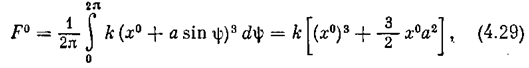
а по формулам (4.17)

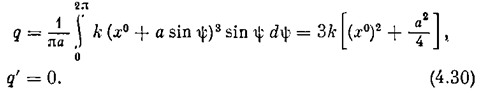
Пример 7. Для петлевой релейной характеристики (рис. 4.5, а) по тем же формулам имеем

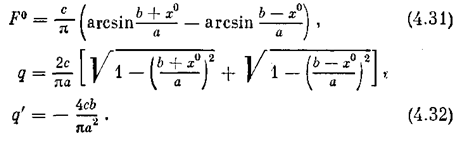
Пример 8. Для характеристики с зоной нечувстви­тельности (рис. 4.1:1) будут иметь место те же выраже­ния F° и q. Графики их представлены на рис. 4.9, а, б. При этом q' == 0. Для идеальной же релейной характе­ристики (рис. 4.10) получаем

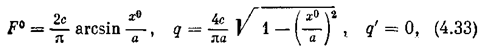
что изображено на рис. 4.10, а и б.

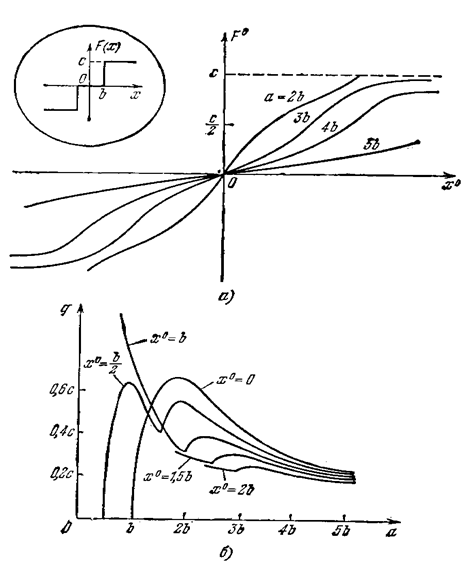
Рис. 4.9.

Пример 9. Для характеристики с линейным участ­ком ц насыщением (рис.4.11,а) при а ³ b+½ x ⁰½ имеем

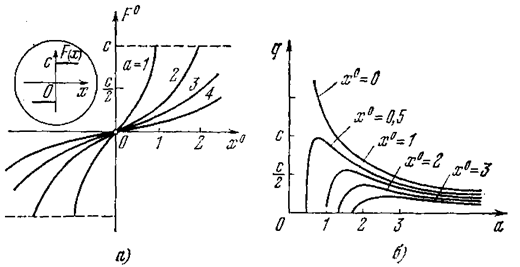
Рис. 4.10.

Эти зависимости представлены в виде графиков на рис. 4.11, б, в.

Пример 10. Для несимметричной характеристики

(рис. 4. 12, а) по формуле (4.l6) находим

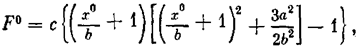
а по формулам (4.17)

Результаты изображены графически на рис. 4.12, б и в.

Рис.4.11.

Полученные в этих примерах выражения и графики коэффициентов гармонической линеаризации будут ис­пользованы ниже при решении задач по исследованию

Рис. 4.12.

автоколебаний, вынужденных колебаний и процессов управления.

Базируясь на свойстве фильтра линейной части системы (лекция 12), ищем периодическое решение нелинейной системы (рис. 4.21) на входе нелинейного элемента приближенно в виде

х = a sin w t (4.50)

с неизвестными а и w. Задана форма нелинейности у = F(x) и передаточная функция линейной части

Производится гармоническая линеаризация нелинейности

что приводит к передаточной функции

Амплитудно-фазовая частотная характеристика разомкнутой цепи системы получает вид

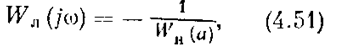
Периодическое решение линеаризованной системы (4.50) получается при наличии в характеристическом уравнении замкнутой системы пары чисто мнимых корней.

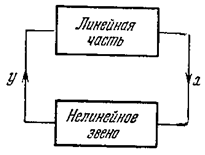
Рис.4.21.

А это по критерию Найквиста соответствует прохождению W (j w) через точку -1. Следо­вательно, периодическое реше­ние (4.50) определяется равен­ством

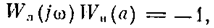
или

где

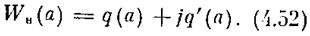
Уравнение (4.51) определяет искомые амплитуду а и частоту w периодического решения. Это уравнение ре­шается графически следующим образом. На комплексной плоскости (U, V) вычерчивается амплитудно-фазовая частотная характеристика линейной части Wл(j w)(рис. 4.22), а также обратная амплитудно-фазовая ха­рактеристика нелинейности с обратным знаком -1 / Wн(a). Точка В их пересечения (рис. 4.22) и определяет величи­ны а и w, причем значение а отсчитывается по кривой -1 / Wн (a), а значение w — по кривой Wл (jw).

Вместо этого можно пользоваться двумя скалярными уравнениями, вытекающими из (4.51) и (4.52):

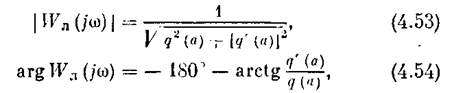
которые также определяют две искомые величины а и w.

Последними двумя уравнениями удобнее пользоваться в логарифмическом масштабе, привлекая логарифмические­

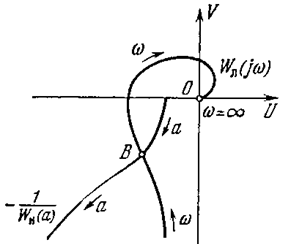
Рис. 4.22.

частотные характери­стики линейной части. Тогда вместо (4.53) и (4.54) будем иметь следующие два урав­нения:

На рис. 4.23 слева изображены графики левых частей уравнений (4.55) и (4.56), а справа—правых частей этих уравнений. При этом по оси абсцисс слева часто­та w откладывается, как обычно, в логарифмическом масштабе, а справа—амплитуда а в натуральном масш­табе. Решением этих уравнений будут такие значения а и w, чтобы при них одновременно соблюдались оба ра­венства: (4.55) и (4.56). Такое решение показано на рис. 4.23 тонкими линиями в виде прямоугольника.

Очевидно, что сразу угадать это решение не удастся. Поэтому делаются попытки, показанные штриховыми линиями. Последние точки этих пробных прямоугольников М1 и М2 не попадают на фазовую характеристику нели­нейности. По если они расположены по обе стороны ха­рактеристики, как на рис. 4.23, то решение находится интерполяцией — путем проведения прямой ММ1.

Нахождение периодического решения.упрощается а случае однозначной нелинейности F(х). Тогда q' = 0 и уравнения (4.55) и (4.56) принимают вид

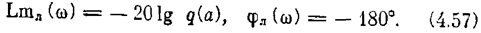
Решение показано на рис. 4.24.

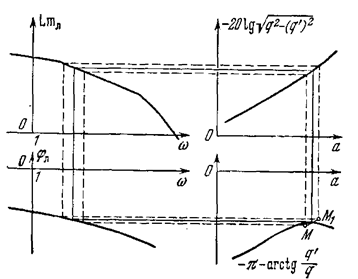
Рис. 4.23.

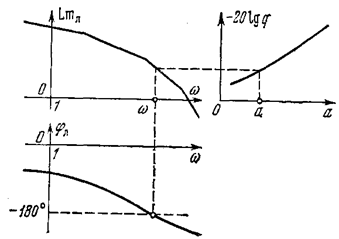
Рис. 4.24.

После определения периодического решения надо ис­следовать его устойчивость. Как уже говорилось, перио­дическое решение имеет место в случае, когда амплитудно-фазовая характеристика разомкнутой цепи

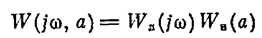
проходит через точку -1. Дадим амплитуде отклонение D а. Система будет возвращаться к периодическому ре­шению, если при D а > 0 колебания затухают, а при D а < 0 — расходятся. Следовательно, при D а > 0 харак­теристика W(jw, а) дол­жна деформироваться (рис. 4.25) так, чтобы при D а > 0 критерий устойчивости Найквиста соблюдался, а при D а < 0 — нарушался.

Итак требуется, что­бы на данной часто­те w было

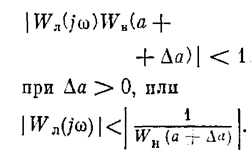
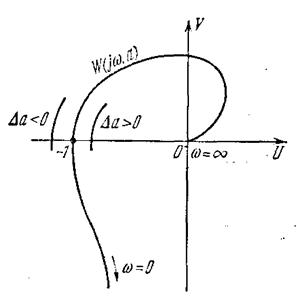
Рис. 4.25.

Отсюда следует, что на рис. 4.22 положительный отсчет амплитуды а вдоль кривой -1/Wн (а) должен быть на­правлен изнутри вовне через кривую Wл (jw), как там и показано стрелкой. В противном случае периодическое решение неустойчиво.

Рассмотрим примеры.

Пусть в следящей системе (рис. 4.13, а) усилитель имеет релейную характеристику (рис. 4.17, а). Па рис. 4.17, б для нее показан график коэффициента гар­монической линеаризации q(а), причем q’(а) =0. Для определения периодического решения частотным спосо­бом, согласно рис. 4.22, надо исследовать выражение

Из формулы (4.24) получаем для данной нелинейности

График этой функции изображен па рис. 4.26.

Передаточная функция линейной части имеет вид

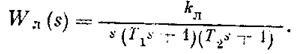
Рис.4.26.

Амплитудно-фазовая характеристика для нее приведена на рис. 4.27. Функция же -1 / Wн (а), являясь в данном слу­чае вещественной (рис. 4.26), укладывается вся на отрица­тельной части вещественной оси (рис. 4.27). При этом на участке изменения амплитуды b £ a £ b 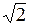амплитуда отсчи­тывается слева извне внутрь кривой Wл(jw), а на участке а > b 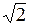— в обратную сторону. Следовательно, первая точка пересечения (а 1) дает неустой­чивое периодическое решение, а вторая (а 2) — устойчивое (ав­токолебания). Это согласуется с прежним решением (пример 2 лекция 15, 16).

Рассмотрим также случай петлевой характеристики реле (рис. 4.28, а) в той же следящей системе (рис. 4.13, а). Амплитудно-фазовая частотная характе­ристика линейной части та же (рис. 4.28, б). Выражение же для кривой –1/Wн(а), согласно (4.52) и (4.23), при­нимает вид

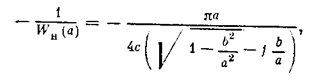
или

Это—прямая, параллельная оси абсцисс (рис. 4.28, б), с отсчетом амплитуды а справа налево. Пересечение даст устойчивое периодическое решение (автоколебания). Чтобы получить графики зависимости амплитуды и частоты

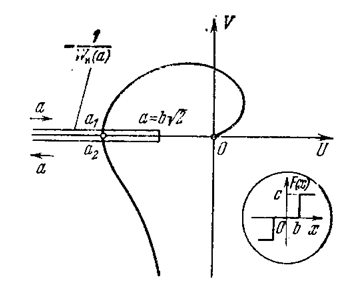
Рис. 4.27.

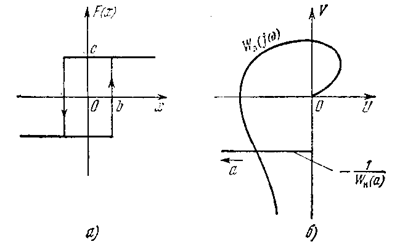
Рис. 4.28.

от k л, представленные на рис. 4.20, нужно на рис. 4.28 построить серию кривых Wл(jw) для каждой величины k л и найти в их точках пересечения с прямой –1/Wн(а) соответствующие значения а и w.

Дата добавления: 2014-11-20