Примеры применения теоремы В.М. Попова

Графическая интерпретация условий теоремы В.М. Попова. Процедура проверки абсолютной устойчивости по В.М. Попову.

Теорема В.М. Попова об абсолютной устойчивости.

Выше мы уже получали условия абсолютной устойчивости в различных случаях. Аналогично для цели исследования абсолютной устойчивости нелинейных систем служит частотный критерий устойчивости В. М. Попова. Он дает достаточные условия абсолютной устойчивости нелинейной системы но виду частотной характеристики линейной части системы.

Пусть в системе имеется одна однозначная нелинейность F(x) (рис. 5.20). Рассмотрим два случая расположения­

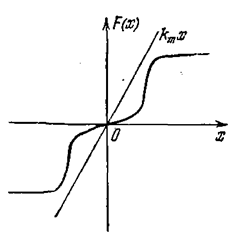
Рис. 5.20.

характеристики: первый — нелинейная характеристика расположена в секторе [0, k m], как на рис. 5.20, второй — в секторе [k0, km], что будет показано ниже.

Начнем с первого случая:

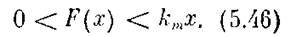
Линейная часть системы описывается уравнением

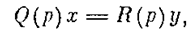
причем степень многочлена Q(p) больше степени многочлена R(p). Передаточная функция линейной части W(s) =R(s) / Q(s) имеет полюсы с отрицательными вещественными частями, причем допускается наличие не более двух нулевых полюсов.

Приведем без доказательства формулировку теоремы В.М.Попова (доказательство см. в [31]).

Теорема Попова. Состояние равновесия нелинейное системы будет абсолютно устойчивым, если нелинейная характеристика находится в секторе [0, km] и существу­ет такое действительное число h, что при всех w ³ 0 выполняется неравенство

где W (jw) — амплитудно-фазовая частотная характери­стика линейной части системы. Для удобства графического представления этого кри­терия вводится модифицированная частотная характери­стика линейной части

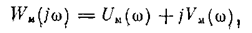
где

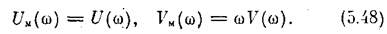
Следовательно, график WM(jw) имеет вид, аналогич­ный амплитудно-фазовой характеристике линейной части W(jw) и отличается от нее только масштабом по мнимой

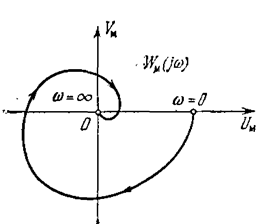
Рис.5.21.

оси (рис. 5.21). Поскольку выражение (5.47) можно записать в виде

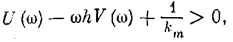
то с подстановкой (5.48) оно преобразуется к виду

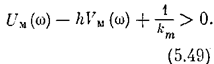
Выражение

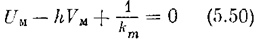
представляет собой уравнение прямой на плоскости пря­моугольных координат Uм, Vм. Эта прямая проходит через точку –1/km на оси Uм и имеет крутизну накло­на 1/h.

Отсюда вытекает следующая формулировка.

Критерий абсолютной устойчивости. Состояние равно­весия нелинейной системы абсолютно устойчиво, если не­линейная характеристика F(x) находится внутри сектора [0, km]и можно провести через точку–1/kmпрямую так, что она не пересечет модифицированную частотную характеристику (последняя лежит справа).

На рис. 5.22 показаны случаи, когда критерий абсо­лютной устойчивости выполняется, а па рис. 5.23 — когда не выполняется.

Интересно получить с помощью этого критерия усло­вия абсолютной устойчивости для той же системы самолета с нелинейным автопилотом, которая была рас­смотрена выше методом Ляпунова (лекция 21) и методом гар­монической линеаризации (лекция 22). Особенность там состоит в том, что допускалось расположение нелинейной характеристики во всей I (и III) четверти, т. е. в секторе [0, km], где km= ¥. Поэтому прямая в частотном крите­рии должна проходить через начало координат.

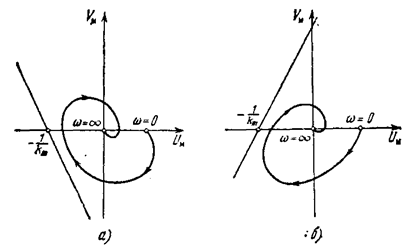
Рис. 5.22.

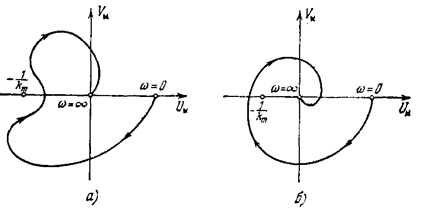
Рис. 5.23.

Решим эту задачу сначала аналитически, а затем проиллюстрируем графически. Условие (5.47) при km = ¥ принимает вид

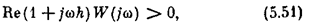
а вместо (5.48) получаем

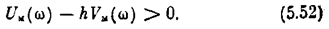
Для указанногопримера (лекция 21) уравнения (5.25) можно преобразовать к виду

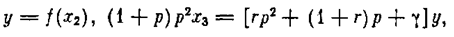
где обозначено у = -р х 2 причем р — операторный сим­вол производной по t(р= d / d t). Передаточная функция линейной части системы записывается в виде

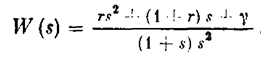
а следовательно,

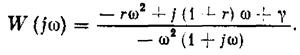
Умножив числитель и знаменатель на 1 — jw, получим

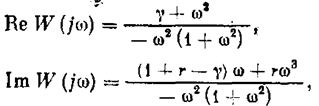
а согласно (5.48)

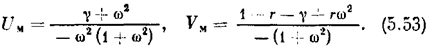
Неравенство (5.52) принимает вид

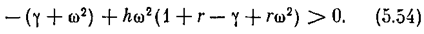
Очевидно, что это неравенство может быть выполнено при любом w ³ 0, если

и если h берется сколь угодно большим, чтобы обеспе­чить неравенство (5.54) при сколь угодномалых w. Полученное условие (5.55) выполняется при

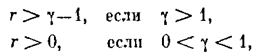
что точно совпадает с найденными ранее условиями аб­солютной устойчивости данной системы (5.28) и (5.24).

Смысл практической реализации этих условий был разъ­яснен в лекции 21).

Графически критерий устойчивости выражается, в том, что вся кривая WM(jw) = Uм(w) + jVм(w), построенная согласно (5.53), расположена (рис. 5.24, а) справа от прямой Uм - h Vм = 0, обозначенной штрих-пунктирной линией, со сколь угодно малым наклоном, если 1+r-g > 0

Рис. 5.24.

Если же 1+г-g<0 (рис. 5.24,б), то такую прямую провести невозможно и, следовательно, нелиней­ная система не будет абсолютно устойчивой.

Здесь был приведен простой пример, и котором усло­вия устойчивости выражаются в аналитическом виде. В большинстве технических задач этого по получится. Однако видно, что описанный частотный критерий устой­чивости в ею графической форме может быть применен для систем с одной однозначной нелинейностью при лю­бой сложности линейной части системы и численно за­данных коэффициентах уравнений.

Перейдем к случаю, когда нелинейная характеристика F(х) расположена в секторе [ko, km], т. е.

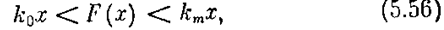
что показано на рbс. 5.25. Здесь неравенство (5.47) в теореме В. М. Попова принимает вид

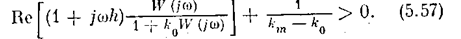
После преобразований приходим к выражению

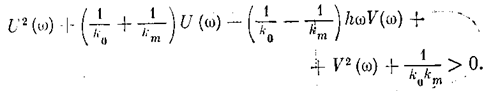
Введя в рассмотрение модифицированную частотную ха­рактеристику (5.48), получаем, что уравнение-

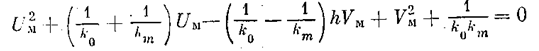
на плоскости координат модифицированной частотной

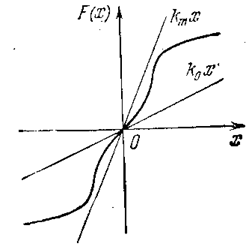
Рис.5.25.

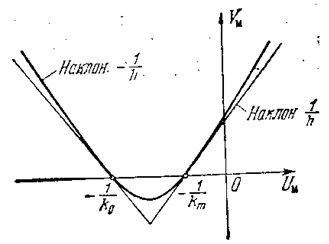
Рис. 5 26.

характеристики (Uм, Vм) дает параболу, проходящую че­рез точки -1/k0 и -1/km и имеющую в этих точках крутизну наклона касательных соответственно -1/h и 1/h.. Построение параболы ясно из рис. 5.26.

Формулировка критерия следующая. Состояние рав­новесия нелинейной системы будет абсолютно устойчиво,

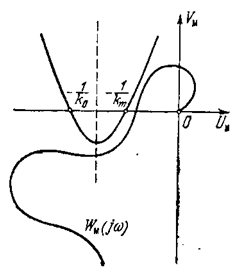
Рис.5.27.

если нелинейная характеристика находится внутрисектора [k0, km] и можно провести через точки -1/ko и -1/km такую параболу с вертикальной осью, чтобы. модифицированная частотная характеристика линейной части лежала вне этой параболы.

Иллюстрация выполнения критерия дана на рис. 5.27, откуда легковидеть, что этот критерий устойчивости дает болееширо­кую область устойчивости чем предыдущий.Видно, что на рис. 5.27 нельзяпровести прямую черезточку -1/km так, чтобыона не пересекала модифицированную частотную характеристику Wм(jw). Следовательно, дан­ная система, абсолютно ус­тойчивая при нелинейности, расположенной в секторе [k0, km], не будет обладать абсолютной устойчивостью (в смысле достаточных условий), если сектор расположе­ния нелинейности расширится до [0, km]. Это вполне естественный результат.

Дата добавления: 2014-11-20