Кривые в плане

При движении автомобиля по кривым в результате действия центробежной силы значительно ухудшаются условия устойчивости автомобиля. Кроме того, водители и пассажиры испытывают существенный дискомфорт из-за наклона автомобиля, а угловая деформация шин (боковой увод), вызванная центробежной силой, сопряжена с повышенным износом шин и расходом топлива. Необходимость снизить влияние этих негативных факторов ложится в основу расчета минимально допустимых значений радиусов круговых кривых в плане.

К центру тяжести автомобиля, движущегося по кривой, приложены две основные поперечные силы:

- центробежная сила (С), направленная горизонтально во внешнюю сторону закругления

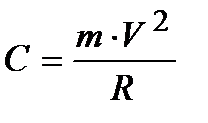, (6)

где m – масса автомобиля, кг; V – скорость автомобиля, м/c; R – радиус кривой, м.

Рис. 6. Схема сил, действующих на автомобиль на кривой

G – составляющая вертикальной нагрузки (веса) от автомобиля на покрытие, параллельная поверхности проезжей части (G_i). Эта составляющая может иметь знак плюс или минус в зависимости от направления уклона проезжей части.

Проецируя обе силы на ось, параллельную поверхности проезжей части, представив G_i как m · g · sin a, получим следующую зависимость:

, (7)

где Y – результирующая сила, стремящаяся сместить автомобиль с дороги и называемая поперечной силой, a – угол наклона проезжей части (tg a = i).

Так как угол a достаточно мал, то можно принять, что cos a» 1, а sin a» tg a = i. Тогда:

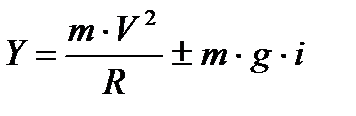. (8)

Преобразовав полученную зависимость, найдем величину радиуса кривой, допустимую из условия ограничения поперечной силы Y:

. (9)

Из зависимости 9. видно, что радиус закругления зависит не от величины поперечной силы, а от его отношения к весу автомобиля . Эту величину назвали коэффициентом поперечной силы. Таким образом зависимость для определения необходимого значения радиуса кривых в плане примет окончательный вид:

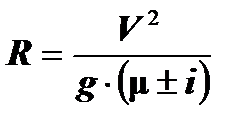. (10)

Величина коэффициента поперечной силы может быть нормирована исходя из различных требований, что отразится на минимально допустимой величине радиуса кривой. Определим эту величину для следующих условий: устойчивость автомобиля против заноса, удобство движения, экономичность движения по криволинейным участкам.

Таким образом, чтобы удовлетворить все перечисленные требования, радиус кривых в плане целесообразно рассчитывать при значении m £ 0,10.

В строительных нормах и правилах для обоснования минимальных радиусов принято m = 0,12 для расчетной скорости 150 км/ч и m = 0,18 для скорости 20 км/ч. В результате в нормах на проектирование приводятся следующие значения радиусов в зависимости от скорости движения (табл.1):

Т а б л и ц а.1

Показатель	Величина показателя
Расчетная скорость, км/ч
Категория дороги	I	II	III	IV	V	-	-	-
Наименьшие радиусы на трудных участках, м

Одновременно строительные нормы рекомендуют во всех случаях, когда это возможно, устраивать кривые с радиусами не менее 3000 м.

Дата добавления: 2014-11-20