Работа газа при изменении его объема

Первое начало термодинамики

Внутренняя энергия системы может изменяться в результате различных процессов, например совершения над системой работы или сообщения ей теплоты. Таким образом, можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте.

Допустим, что некоторая система (газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U ₁,получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией U ₂,совершила работу А над внешней средой. Количество теплоты считается положительным, когда оно подводится к системе, а работа – положительной, когда система совершает ее против внешних сил. Опыт показывает, что в соответствии с законом сохранения энергии при любом способе перехода системы из одного состояния в другое изменение внутренней энергии Δ U=U ₂ - U ₁будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил:

Δ U=Q – A,или

Q= Δ U + A (7.5)

Уравнение (7.5) выражает первое начало термодинамики в интегральной форме: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил.

Выражение (7.5) в дифференциальной форме будет иметь вид:

dQ=dU + dA,

или в более корректной форме:

δQ=dU+δA, (7.6)

где dU – бесконечно малое изменение внутренней энергии системы, δА — элементарная работа, δQ — бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а δА и δQ таковыми не являются. В дальнейшем будем использовать запись первого начала термодинамики в форме (7.6).

Из формулы (7.5) следует, что в системе СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж).

Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии Δ U =0. Тогда, согласно первому началу термодинамики, A = Q, т. е. вечный двигатель первого рода – периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, – невозможен.

Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, находящийся под поршнем в цилиндрическом сосуде (рис.7.1).

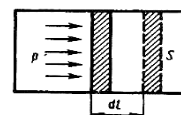Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние d l, то производит над ним работу

δA=Fdl=pSdl=p dV,

где S — площадь поршня, Sdl=dV — изменение

Рис.7.1 объема системы. Таким образом,

δA=p dV (7.7)

Полную работу А, совершаемую газом при изменении его объема от V ₁до V ₂ найдем интегрированием формулы (7.7):

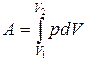(7.8)

Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение справедливо при любых изменениях объема твердых, жидких и газообразных тел.

Рис.7.2

Произведенную при том или ином процессе работу можно изобразить графически с помощью кривой в координатах р, V. Пусть изменение давления газа при его расширении от объема V ₁ до объема V ₂ изображается кривой на рис.7.2.

При увеличении объема на dV совершаемая газом работа равна pdV,т. е. определяется площадью полоски с основанием dV,заштрихованной на рис.7.2. Поэтому полная работа, совершаемая газом при расширении от объема V ₁до объема V ₂ определяется площадью, ограниченной осью абсцисс, кривой p=f (V)и прямыми V ₁и V ₂.

Графически можно изображать только равновесные процессы – процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесны (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медленнее процесс протекает, тем он ближе к равновесному). В дальнейшем рассматриваемые процессы будем считать равновесными.

Дата добавления: 2014-12-08