
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
II. Решение задач. Домашнее задание: повторить материал пунктов 105–112; решить задачи №№ 1107, 1132, 1137
Ход уроков
IV. Итоги урока.
Домашнее задание: повторить материал пунктов 105–112; решить задачи №№ 1107, 1132, 1137.
Уроки 9–10
Решение задач по материалу главы XII
Цели: закрепить знания и умения учащихся по изученному материалу главы; подготовить учащихся к контрольной работе.
I. Математический диктант (15 мин).
Вариант I
1. Площадь круга равна S. Найдите длину ограничивающей его окружности.
2. Найдите длину дуги окружности радиуса 9 м, если градусная мера дуги равна 120°.
3. Длина дуги окружности равна 3π, а ее радиус равен 8. Найдите градусную меру этой дуги.
4. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.
5. Найдите площадь кругового сектора радиуса 4 см, если его центральный угол равен 45°.
6. Площадь кругового сектора равна 18π м2, а его центральный угол равен 40°. Найдите радиус сектора.
Вариант II
1. Длина окружности равна С. Найдите площадь ограниченного ею круга.
2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 25 и 24 см.
3. Найдите площадь кругового сектора радиуса 3 см, если его центральный угол равен 20°.
4. Площадь кругового сектора равна 10π м2, а его радиус равен 6 м. Найдите центральный угол сектора.
5. Найдите длину дуги окружности радиуса 6 дм, если ее градусная мера равна 120°.
6. Найдите радиус окружности, если длина дуги окружности равна 6π, а ее градусная мера равна 60°.
1. Решить задачу 1. Докажите, что площадь S треугольника АВС вычисляется по формуле:
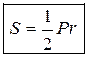 ,
,
где Р – периметр треугольника, r – радиус вписанной окружности.
Доказательство
Пусть О – центр окружности, которая вписана в треугольник АВС и, следовательно, касается сторон треугольника в точках М, N и K.

| Очевидно, что S = SАОС + SВОС + SАОВ. *
Так как ОМ, ОN и ОK – высоты треугольников АОС, ВОС и АОВ, то
SАОС = 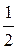 АС · ОK,
SВОС = АС · ОK,
SВОС = 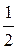 ВС · ОМ и SАОВ = ВС · ОМ и SАОВ = 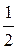 АВ · ОN.
Подставив эти значения в формулу *, получим: S = АВ · ОN.
Подставив эти значения в формулу *, получим: S = 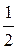 (AB + BC + CA) · r = (AB + BC + CA) · r = 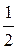 P · r. P · r.
|
2. Решить задачу 2. даны стороны треугольника АВС – а, b, с и площадь S. Выразить радиусы окружностей, описанной около треугольника и вписанной в него, через а, b, с и S.
Решение
1) Используем результат задачи 1:
S = 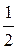 Pr, где Р – периметр треугольника, r – радиус вписанной окружности. Р = а + b + с; 2 S = r (а + b + c), отсюда:
Pr, где Р – периметр треугольника, r – радиус вписанной окружности. Р = а + b + с; 2 S = r (а + b + c), отсюда:

2) Радиус R описанной окружности вычисляется по формуле:
R =  , где – угол, противолежащий стороне а.
, где – угол, противолежащий стороне а.
Из формулы: S = 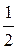 bc · sin получим sin =
bc · sin получим sin = 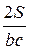 , тогда 2sin =
, тогда 2sin = 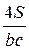 . Следовательно, R =
. Следовательно, R =  .
. 
3. Решить задачу № 1099 на доске и в тетрадях.
Решение
Диагонали А 3 А 7 и А 4 А 8 четырехугольника А 3 А 4 А 7 А 8 являются диаметрами окружности, в которую вписан данный восьмиугольник, поэтому они равны и точкой пересечения О делятся пополам. Следовательно, четырехугольник А 3 А 4 А 7 А 8 – прямоугольник. Так как угол А 3 ОА 4 = 45°, то согласно задаче 1059 площадь прямоугольника равна 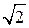 R 2.
R 2.
4. Решить задачу № 1105 (в) (объясняет учитель).
Решение
Пусть АВС – данный треугольник, угол С = 90°, угол В = , АВ = с, ВС = а, СА = b; Р = а + b + с, r – радиус вписанной окружности. Тогда а = с · cos , b = c · sin .
Воспользуемся двумя формулами для вычисления площади S треугольника АВС (метод площадей):

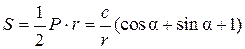 . Отсюда, получаем,
. Отсюда, получаем,
r = 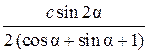 , поэтому C = 2π r =
, поэтому C = 2π r = 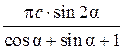 .
.
Умножив числитель и знаменатель дроби на cos + sin – 1, после несложных преобразований получаем: c = π c (sin + cos – 1).
5. Решить задачу № 1117 (в).
решение
Применим метод площадей, то есть воспользуемся двумя формулами для вычисления площади треугольника:
S = 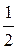 ab sin и S =
ab sin и S = 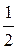 Pr, где а и b – длины сторон треугольника, – угол между ними, Р – периметр, r – радиус вписанной окружности. Получим:
Pr, где а и b – длины сторон треугольника, – угол между ними, Р – периметр, r – радиус вписанной окружности. Получим:
S = 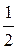 a 2 sin и S = r · а
a 2 sin и S = r · а 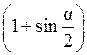 .
.
Отсюда находим r, а затем площадь круга:
S круга = 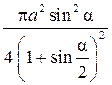 .
.
6. Решить задачи № 1110, 1138, 1116 (в).
Примечание. решения некоторых из них полезно предварительно обсудить, а затем записать в тетрадях, остальные задачи учащиеся могут решить самостоятельно с последующей проверкой ответов или решений.
|
|
Дата добавления: 2014-12-08; Просмотров: 1280; Нарушение авторских прав?; Мы поможем в написании вашей работы!