Ход урока. II. Построение правильных многоугольников

III. Итоги урока.

II. Построение правильных многоугольников.

I. Проверка домашнего задания.

Ход урока

IV. Итоги урока.

Задание на дом: изучить материал пункта 108; решить задачи №№ 1087, 1088, 1094 (а, б).

Урок 4
Построение правильных многоугольников

Цель: выработать у учащихся умение строить некоторые правильные многоугольники.

1. Проверить решение учащимися задач № 1087 и № 1088 по тетрадям.

2. Решить на доске часть заданий, вызвавших затруднения у учащихся.

1. Рассмотреть решение задачи 1 пункта 109.

2. Построение правильного треугольника, вписанного в окружность.

3. Рассмотреть решение задачи 2 пункта 109.

4. Построение правильного двенадцатиугольника, вписанного в окружность (рис. 310).

5. Построение правильных четырехугольника, восьмиугольника, шестнадцатиугольника, вписанных в окружность.

6. Построение правильных шестиугольника, треугольника, описанных около окружности.

7. Построение правильных четырехугольника, восьмиугольника, описанных около окружности.

Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Оказывается, что не все правильные многоугольники допускают такое построение. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.

Однако с помощью этих инструментов можно построить правильный семнадцатиугольник.

Домашнее задание: выполнить аналогичное задание на чертежных листах (построение правильных многоугольников, вписанных в окружность, и построение правильных многоугольников, описанных около окружности).

Учитель может указать количество сторон правильного многоугольника. Лучшие работы пойдут в методическую копилку.

Решить задачи №№ 1095, 1096, 1097.

Урок 5
Длина окружности

Цели: вывести формулу, выражающую длину окружности через ее радиус; вывести формулу для вычисления длины l дуги окружности с градусной мерой ; закрепить знание формул при решении задач.

I. Математический диктант (15 мин).

Вариант I

1. Найдите угол правильного десятиугольника.

2. Найдите сторону правильного треугольника, если радиус описанной около него окружности равен 2 м.

3. Найдите радиус окружности, вписанной в правильный треугольник, если радиус описанной около него окружности равен 2 м.

4. Найдите площадь правильного треугольника, если расстояние от его центра до вершины равно 2 м.

5. Закончите предложение: «Угол с вершиной в центре окружности называется …»

6. Угол с вершиной в центре правильного многоугольника и сторонами, проходящими через две его соседние вершины, равен 36°. Сколько сторон имеет этот многоугольник?

7. Чему равен cos 0°?

8. С помощью циркуля и линейки постройте правильный шестиугольник.

Вариант II

1. Сколько сторон имеет правильный многоугольник, если его сторона стягивает дугу описанной окружности, равную 18°?

2. Найдите площадь квадрата, если радиус описанной около него окружности равен 2 дм.

3. Закончите предложение: «Кругом называется часть плоскости …»

4. Найдите сторону квадрата, если расстояние от его центра до вершины равно 2 дм.

5. Найдите радиус окружности, вписанной в квадрат, если радиус описанной около него окружности равен 2 дм.

6. Чему равен cos 0°?

7. Найдите угол правильного девятиугольника.

8. С помощью циркуля и линейки постройте правильный треугольник.

II. Изучение нового материала (лекция).

Поскольку материал пункта «Длина окружности» нетрадиционен и опирается на понятие предела, его изложение целесообразно дать в форме лекции.

1. Дать представление о длине окружности с помощью нитки, обмотанной около дна стакана.

2. Работа по рисункам 312 и 313 учебника.

3. Вывод формулы, выражающей длину окружности через ее радиус.

4. Записать в тетради вывод: отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Число π (пи).

5. Формула для вычисления длины окружности: C = 2π R; d = 2 R, тогда C = π d, где d – диаметр окружности.

Найдем радиус и диаметр окружности: R = 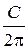; d = 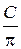, где π ≈ 3,14.

6. Вывод формулы для вычисления длины l дуги окружности с градусной мерой :

длина дуги в 1° равна ;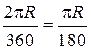

длина дуги в ° равна l = ∙ .

III. Закрепление изученного материала (решение задач).

1. Решить задачу № 1101 (таблицу начертить заранее на доске).

2. Устно решить задачи № 1102 и № 1103.

3. Решить задачу № 1109 (а, б).

4. Решить задачу № 1111 (использовать рис. 316).

Дата добавления: 2014-12-08