Метод наименьших квадратов

Рассмотрим опыт по определе­нию модуля растяжения метал­лического стержня. Результаты измерений удлинения стержня под нагрузкой могут быть представлены в виде таблицы.

Нагрузка	Xl	X2	…	Хn
Удлинение	Y1|	Y2	…	Yn

Согласно закону Гука зависимость удлинения от нагрузки имеет вид

y=kx (13).

Неизбежные ошибки опыта приводят, однако, к тому, что точки (х_i, у_i) не лежат на одной прямой. Значение к может быть найдено из любой пары значений (х_i, у_i) а наличие n пар приводит к появлению n, вообще говоря, несовместных уравнений для нахождения k.

Задачу о выборе наилучшего значения можно решать графически, отмечая точки на миллиметровой бумаге и проводя через них на глаз наилучшую прямую. Графический способ решения не всегда, однако, обеспечивает достаточную точность. Аналитическое решение задачи производится с помощью метода наименьших квадратов. Сущность метода такова. Рассмотрим отклонение точек (х_i, у_i) от прямой (13) и составим величину j – сумму квадратов вертикальных отклонений наших точек от прямой:

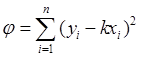(14).

Величина j всегда положительна и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для k следует выбирать такое его значение, при котором j имеет минимум.

Дифференцируя j, найдем:

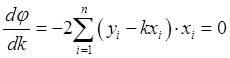
или

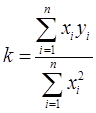(15)

Вычисление показывает, что стандартная ошибка s(k) определения величины k равна при этом

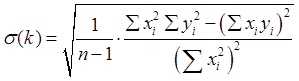(16)

Мы рассмотрели сейчас наиболее простой случай применения метода наименьших квадратов. Рассмотрим теперь несколько более трудный случай, когда точки должны удов­летворять не формуле (13), а несколько более сложной формуле

у=а+b×х (17)

Задача состоит в том, чтобы по имеющемуся набору значений (х_i,y_i) найти наилучшие значения а и b.

Снова составим квадратичную форму, равную сумме квадратов отклонений точек от закона(17),

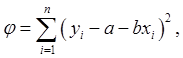
и найдем значения а и b, при которых имеет минимум j:

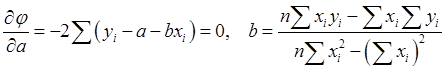
Совместное решение этих уравнений дает

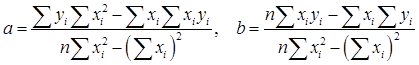(18).

Формулы (18) принимают более простой вид, если ввести :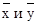

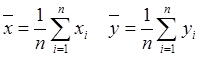(19).

Подстановка (19) в (18) дает

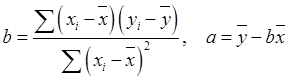(20)

Стандартные ошибки определения a и b равны:

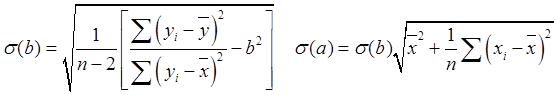(21).

Формулы (15) и (20) дают аналитический способ проведения прямой через заданные экспериментальные точки.

Критерии значимости. Метод c²

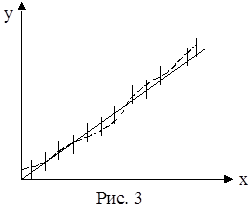
Вернемся к опыту по исследованию упругих свойств металлического стержня. Пусть ре­зультаты опытов изображаются точками на рис.3. Первый же взгляд на график убеждает нас в том, что зависимость удлинения от нагрузки является линейной или почти линейной. На самом деле, прямая, проведенная на рис.3 сплошной линией, не противоречит эксперимен­тальным данным. Им не противоречит, однако, и изогнутая линия. Более того, эта линия даже несколько лучше удовле­творяет экспериментальным данным, чем пря­мая. Мы хотели бы, однако, думать, что истин­ная связь удлинения и на­грузки все-таки являет­ся прямолинейной. Задача сводится к отыска­нию критерия, позволяющего судить о том, яв­ляется ли представление иско­мой зависимости в виде прямой ли­нии достаточно хорошим или экспериментальные данные заставляют отдать предпочтение криволинейной зависимости.

Сформулированная сейчас задача в применении к закону Гука представляется несколько искусственной. В этом случае лучше всего попросту повторить опыт, уменьшив экспери­ментальные ошибки, и вопрос решится сам собой. Встречаются, однако, случаи, когда та­кое повторение опыта является затруднительным или даже невозможным. Так бывает, на­пример, при опытах с редкими частицами в космических лучах или на ускорителях, когда повторение опыта требует нескольких лет работы или попросту оказывается невозможным. Возможно более полная интерпретация имеющихся данных становится в этом случае особенно существенной.

Общий вопрос, который возникает в таких случаях, сводится обычно к следующему. На графике, изображающем некоторую зависимость, точки легли не вполне регулярно. Следует ли предавать значение наблюденным отступлениям от гладкой кривой? Совместима ли с экспериментальными данными гипотеза о том, что искомая зависимость на самом деле является гладкой (или даже прямолинейной) или эти данные указывают на негладкий ход кривой? Исследование проблемы достоверности гипотез производится обычно с помощью критериев значимости. Одним из наиболее удобных критериев значимости является так называемый «критерий c²».

В предыдущем разделе мы рассматривали метод наименьших квадратов, с помощью которого можно, например, провести через экспериментальные точки наилучшую прямую. Исследуем теперь вопрос о том, насколько данные, использованные для проведения этой прямой, согласуются с представлением о том, что рассматриваемая прямолинейная зави­симость действительно имеет место. Единственной мерой, которая может быть использова­на для расчета, является естественно, точность, с которой экспериментальные точки удов­летворяют предполагаемому закону. В методе c² в качестве такой меры принимается сумма квадратов отклонений от предполагаемой зависимости

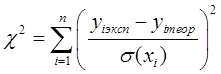(22).

Отклонения экспериментальных точек от значений, следующих из принятой гипотезы, выражаются в долях стандартной ошибки данного измерения s(x_i). Найденное значение c² должно быть сопоставлено с теорией. Это делается с помощью таблицы. В таблице для разного числа n степеней свободы приведены значения c² для ряда чисел p. Числом степеней свободы n в этом случае называется число измерений без одного, если гипотеза не содержит определяемых из опыта коэффициентов, число измерений без двух, если из опыта находится один коэффициент, например, наклон прямой и т.д. Для 10 степеней свободы находим из таблицы, что c² =2,6 для р=99, c²=3,9 для р =95, c²=7,3 для р=70, c² =23,2 для р=1 и т.д. Это означает, что в том случае, если гипотеза справедлива, рассчитанное по (22) значение c² с вероятностью 99% (р=99) окажется больше 2,6, с вероятностью 95% (р=95) больше 3,9, с вероятностью 70% больше 7,3, с вероятностью 1% больше 23,2 и т.д. Пусть мы найдем в результате расчета по формуле (22) c²=3,5. Такое значение c² должно наблюдаться больше чем в 95% случаев; отклонение наших данных от прямолинейной зависимости является в этом случае совершенно несущественным. Если бы мы нашли в результате расчета c² =18, сопоставление с таблицей показало бы нам, что такие отклонения следует ожидать только в 5 % случаев. Существование прямолинейной зависимости и в этом случае нельзя считать исключенным, но оно должно быть поставлено под сомнение. Естественно в этом случае по­вто­рить опыт, чтобы получить более ясный результат. Если бы c² оказалось равно 30 (вероятность получить на опыте такое значение равна 0,1%) можно было бы утверждать, что проверяемая гипотеза почти наверное является ошибочной.

При сравнении отклонений с таблицей обычно применяют следующую терминологию: если найденная из опыта величина c² должна наблюдаться с вероятностью, заключенной между 1% и 5% отклонения называются почти значимыми, если вероятность заключена между 0,1 и 1% - значимыми и, наконец, если вероятность обнаружить найденное значение c² оказывается меньше 0,1%, отклонения являются высокозначимыми. При вероятности большей 5% следует считать, что экспериментальные данные недостаточны для того, чтобы отвергнуть эту гипотезу.

На этом мы заканчиваем краткое изложение методов обработки наблюдений. Более подробные сведения могут быть найдены в специальных книгах.

Распределение c²

Р - вероятность (в%) найти на опыте значение c², большее чем указано в таблице, n – число степеней свободы системы.

n \ p														0,1
	0.3	0,4	0.7	1,1	1,6	2,2	3,4	4.9	6.0	7,8	9.5	11,7	13,3	18.5
	0,6	0,8	1,1	1,6	2,3	3.0	4,4	6,1	7,3	9-2	11,1	13,4	15,1	20,5
	0,9	1,1	1,6	2 2	3,1	3,8	5,3	7 ^	8.6	10,6	12,6	15,0	16,8	22,5
	1-2	1.6	2,2	2,8	3.8	4,7	6,3	8,4	9,8	12,0	14,1	16,6	18,5	24,3
	1-6	2,0	2.7	3,5	4,6	5,5	7.3	9,5	11.0	13,4	15,5	18,2	20.1	26,1
	2.1	2,5	3.3	4,2	5.4	6,4	8.3	10,7	12,2	14,7	16.9	19,7	21,7	27,9
	2,6	3-1	3.9	4,9	6,2	7,3	9,3	11,8	13,4	16.0	18,3	21-2	23,2	29.6
	3,1	3.6	4,6	5,6	7,0	8,1	10,3	12,9	14,6	17,3	19,7	22.6	24.7	31,3
	3,6	4,2	5.2	6,3	7,8	9,0	11,3	14.0	15,8	18,5	21.0	24.1	26,2	32.9
	4.1	4.8	5,9	7.0	8,6	9.9	12,3	15.1	17.0	19.8	22.4	25.5	27.7	34.5
	4,7	5,4	6,6	7,8	9,5	10,8	13,3	16.2	18.1	21.1	23.7	26,9	29,1	36,1 1
	5,2	6.0	7,3	8,5	10,3	11,7	14,3	17,3	19,3	22,3	25,0	28.3	30,6	37,7
	5,8	6,6	8,0	9,3	11,1	12,6	15,3	18,4	20,5	23,5	26,3	29,6	32,0	39,2
	6,4	7,3	8,7	10,1	12,0	13,5	16,3	19,5	21,6	24,8	27,6	31,0	33,4	40,8
	7,0	7,9	9.4	10,9	12,9	14,4	17,3	20,6	22.8	26,0	28,9	32,3	34,8	42.3
	7.6	8.6	10,1	11,6	13,7	15,4	18.3	21,7	23.9	27.2	30,1	33,7	36.2	43,8
	8-3	9,2	10,8	12,4	14,6	16,3	19,3	22,8	25,0	28,4	31,4	35,0	37,6	45,3
	8-9	9,9	11,6	13,2	15,4	17,2	20,3	23,9	26,2	29,6	32,7	36,3	38,9	46,8
	9.5	10,6	12,3	14,0	16,3	18.1	21,3	24,9	27.3	30.8	33.9	37.7	40.3	48,3
	10,2	11,3	13,1	14,8	17,2	19,0	22,3	26,0	28„4	32,0	35.2	39,0	41,6	49,7
	10,9	12,0	13,8	15,7	18,1	19,9	23,3	27,1	29,6	33.2	36,4	40,3	43,0	51,2
	11,5	12,7	14,6	16,5	18,9	20,9	24,3	28,2	30,7	34,4	j 37,7	41,6	44,3	52.6
		13,4	15,4	17,3	19,8	21,8	25,3	29,2	31.8	35,6	38,9	42,9	45,6	54,0
	12.9	14,1	16.1	18,1	20,7	22,7	26,3	30,3	32,9	36,7	40,1	44,1	47.0	55,5
	13,6	14,8	16.9	18,9	21,6	23,6	27,3	31,4	34,0	37,9	41,3	45,4	48,3	56,9
	14,3	15,6	17,7	19,8	22,5	24,6	28,3	32,5	35,1	39,1	42,6	46,7	49,6	58,3
	15,0	16.3	18,5	20,6	23,4	25,5	29,3	33,5	36,2	40,3	43,8	48,0	50,9	59,7

Дата добавления: 2014-11-29