ВВЕДЕНИЕ. Цель работы: ознакомиться со статистическими закономерностями процесса радиоактивного распада, определить характеристики распределения Пуассона для

СТАТИСТИЧЕСКИЙ ХАРАКТЕР РАДИОАКТИВНОГО РАСПАДА

РАБОТА № 5

Цель работы: ознакомиться со статистическими закономерностями процесса радиоактивного распада, определить характеристики распределения Пуассона для конкретного случая.

Приборы и принадлежности: бета активный препарат, пересчетный прибор.

Измерение макроскопических величин (например, массы какого-либо тела, длины стержня и т.д.) производится с той или иной степенью точности. Это обусловлено как точностью прибора, так и особенностями самого процесса измерения. Поэтому можно сказать, что сама по себе измеряемая величина (масса, длина стержня и т.д.) имеет некоторое волне определенное значение, в то время как результаты измерений флуктуируют из-за несовер­шенства измерительных приборов, недостаточной их изоляции от внешних условий и т.д. Совсем иначе обстоит дело со многими измерениями в ядерной физике. В отличие от мак­ромира флуктуации измеряемых величин связаны, как правило, с самой сутью явлений и поэтому не могут быть сделаны сколь угодно малыми. Так, если речь идет об измерении числа актов радиоактивного распада, происшедших за какое-то время, то флуктуирует сама измеряемая величина, а измерительный прибор (счетчик частиц) в первом приближении можно считать идеальным, то есть не подверженным статистическому влиянию окружаю­щих условий.

Роль статистического подхода к явлениям микромира значительно глубже, чем в макро­мире. Статистика здесь нужна не только для обработки результатов измерений, но и для изучения самой природы исследуемых явлений. Например, природа радиоактивности была окончательно установлена только после завершения подробного статистического анализа, показавшего, что различные акты распада между собой статистически независимы. По­следнее означает, что момент распада определенного ядра радиоактивного изотопа не за­висит ни от предыстории источника излучения, ни от состояния атомов, находящихся в окрестностях рассматриваемого атома.

Поскольку каждый акт распада является случайным событием, то в течение определенного интервала времени t распадается различное число ядер. Если обозначить через N_i число распадов, зарегистрированных за время t в i-том измерении, то не все N_i будут одинаковыми. Однако большинство этих величин будет близко к среднему значению áNñ:

áNñ=(N_{1 +} N₂ +... + N_k) / k

(здесь k - число измерений).

Чем больше отличие N_i от áNñ, тем меньше Р(N_i)- вероятность обнаружить это значение N_i:

(25).

Формула (25) называется распределением Пуассона. Из (25) можно найти среднеквадратичное отклонение[10] DN числа зарегистрированных распадов от áNñ:

DN= 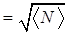(26)

и относительное отклонение dN:

dN= DN /<N>= (27).

Если áNñ велико (áNñ>>1), то различные значения N_i можно считать распределенными непрерывно. В этом случае распределение Пуассона переходит в распределение Гаусса:

dW(N) = F(N) dN = 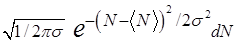(28),

где F(N) = 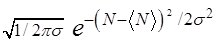(29)

- функция распределения Гаусса. s = 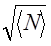- среднеквадратичное отклонение N от <N>. Произведение F(N)×dN = dW(N) есть вероятность того, что значение измеренной величины N лежит в пределах от N до N + dN. Вывод соотношений (25), (26), (28) дан в Приложении к работе.

В настоящей работе изучается статистика бета распада и проверяется распределение Гаусса (28). Для этого необходимо провести достаточно большое число наблюдений актов распада, происходящих в течение определенного времени, и вычислить вероятность того или иного значения числа распадов, а затем сравнить ее с вероятностью, даваемой соотношением (28).

Дата добавления: 2014-11-29