Основные понятия комбинаторики

Размещения. Пусть имеется мно­жество, содержащее n элементов. Каждое его упорядоченное подмножество, содержащее n элементов, называется размещением из n элементов по m эле­ментов.

Из определения вытекает, что 0 < m < n и что размещения из n элемен­тов по m - это все m-элементные подмножества, отличающиеся составом элементов или порядком их следования.

Число размещений из я элементов по т элементов в каждом обозначают и вычисляют по формуле

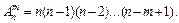
Число размещений из n элементов по m элементов в каждом равно произ­ведению m последовательно убывающих натуральных чисел, из которых боль­шее есть n.

Для краткости произведение первых n натуральных чисел принято обоз­начать n! (n-факториал):

1 • 2 • 3... n=n!

Условились считать, что 0! = 1.

Тогда формулу числа размещений из n элементов по m элементов можно записать и в другом виде: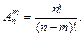

Пример 2. Сколькими способами собрание, состоящее из 30 человек, может выбрать из присутствующих президиум в составе председателя, сек­ретаря и члена президиума?

Решение. Состав президиума собрания является упорядоченным мно­жеством из 30 элементов по три элемента. Значит, искомое число способов равно числу размещений из 30 элементов по три элемента в каждом:

или

Перестановки. Размещения из n элементов по n элементов называ­ются перестановками из n элементов.

Из определения следует, что перестановки являются частным случаем размещений. Так как каждая перестановка содержит все n элементов мно­жества, то различные перестановки отличаются друг от друга только поряд­ком элементов.

Число перестановок из n элементов данного множества обозначают Р_n, а вычисляют по формуле

Р_n = 1•2•3... n=n!

Пример 3. Сколько четырехзначных чисел можно составить из четырех цифр 1, 2, 3, 4 без повторений?

Решение. По условию дано множество из четырех элементов, которые требуется расположить в определенном порядке. Значит, требуется найти количество перестановок из четырех элементов:

Р_n = 1•2•3•4 = 24,

т. е. из цифр 1, 2, 3, 4 можно составить 24 четырехзначных числа (без повто­рений цифр).

Сочетания. Пусть имеется множество, состоящее из n элементов. Каждое его подмножество, содержащее т элементов, называется сочетанием из n элементов по m элементов.

Таким образом, сочетания из n элементов по m элементов - это все m-элементные подмножества, которые имеют одинаковый состав элементов. Под­множества, отличающиеся друг от друга порядком следования элементов, не считаются различными.

Число подмножеств по m элементов в каждом, содержащихся во мно­жестве из n элементов, т. е. число сочетаний из n элементов по m элементов в каждом, обозначают 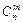и вычисляют по формуле

или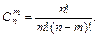

Число сочетаний 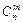обладает свойством 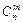= 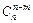(0 < m < n). Так,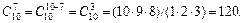

Пример 4. Сколькими способами можно распределить 12 человек по бригадам, если в каждой бригаде по 6 человек?

Решение. Состав каждой бригады является конечным множеством из 12 элементов по 6. Значит, искомое число способов равно числу сочетаний из 12 элементов по 6 в каждом:

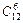= (12 • 11 • 10 • 9 • 8 • 7)/(1 • 2 • 3 • 4 • 5 • 6) = 924.

Примеры непосредственного вычисления вероятностей.

Пример 5. В урне находятся 6 белых и 5 черных шаров. Из урны одно­временно вынимают два шара. Какова вероятность того, что оба шара белые (событие А)?

Решение. Здесь число равновозможных независимых исходов состав­ляет n = = (11 • 10)/(1 • 2) = 55. Событию А благоприятствуют 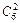=(6•5)/(1•2)=15 исходов. Следовательно, Р (А) = 15/55 = 3/11.

Пример 6. В партии из 20 изделий четыре бракованных. Найти вероят­ность того, что среди пяти взятых наугад изделий окажется два бракованных (событие В).

Решение. Здесь число равновозможных независимых исходов есть

n = 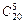= (20•19•18•17•16)/(1•2•3•4•5)= 15504.

Подсчитаем число исходов m, благоприятствующих событию В. Среди пяти взятых изделий окажется два бракованных и три стандартных. Два бра­кованных изделия из четырех можно выбрать 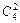=(4 • 3)/(1 • 2) = 6 способами, а три стандартных изделия из 16 можно выбрать 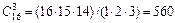способами. Каждая комбинация бракованных изделий может сочетаться с каждой комбинацией стандартных изделий, поэтому m=560•6=3360. Следовательно, Р(В) = 3360/15504 =70/323»0,2.

Пример 7. Девять различных книг расставлены наудачу на одной полке. Найти вероятность того, что четыре определенные книги окажутся поставленными рядом (событие С).

Решение. Здесь число равновозможных независимых исходов есть n=Р₉=9!. Подсчитаем число исходов m, благоприятствующих событию C. Представим себе, что четыре определенные книги связаны вместе. Тогда эту связку можно расположить на полке Р₆= 6!. способами (связка плюс остальные пять книг). Внутри связки четыре книги можно переставлять Р₄=4! способами. При этом каждая комбинация внутри связки может сочетаться с каждым из Р₆ способов образования связки, т. е. m= Р₆ • Р₄. Следовательно Р(С) = (Р₆ •Р₄)Р₉=1/21.

Дата добавления: 2014-12-08