Вопросы для самопроверки. 1. Дайте определение определенного интеграла

1. Дайте определение определенного интеграла.

2. Перечислите основные свойства определенного интеграла.

3. В чем заключается геометрический смысл определенного интеграла?

4. Напишите формулы для определения площади плоской фигуры с по­мощью определенного интеграла.

5. По каким формулам находится объем тела вращения?

6. Напишите формулу для вычисления пути, пройденного телом.

7. Напишите формулу для вычисления работы переменной силы.

8. По какой формуле вычисляется сила давления жидкости на пластинку?

Производная и ее приложения

Производная. Понятие производной является одним из важнейших в курсе математики. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.

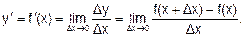Производной функции y=f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.

Если у=f(u) и u=φ(x)— дифференцируемые функции своих аргумен­тов, то производная сложной функции у=f(φ(x)) существует и равна произ­ведению производной функции у по промежуточному аргументу u на произ­водную промежуточного аргумента u по независимой переменной х:

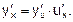Аналогичная формула верна и для сложных функций, которые задаются с помощью цепочки, содержащей три звена и более.

Таблица формул дифференцирования

1. с’=0

2. х’=1

3. (u±v)’ = u’ ± v’

4. (uv)’ = uv’ + vu’

5. (cu)’ = cu’

6.

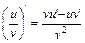
7.

8.

9.

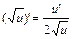
10. (a^u)’ = a^u ln a • u’

11. (e^u)’ = e^u ln eu’ = e^uu’

12. где u>0

13. где u>0

14. (sin u)’ = cos u • u’

15. (cos u)’ = - sin u • u’

16.

17.

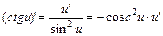
18.

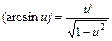
19.

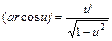
20.

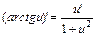
21.

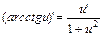
Здесь u и v — дифференцируемые функции от х, а

с - постоянная величина.

Пример 1. Найти производную функции

Решение. Дифференцируем функцию по формулам

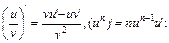
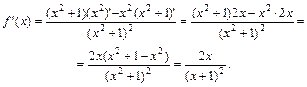
Пример 2. Найти производную функции у=sin³j и вычислить ее значе­ние при j= p/3.

Решение. Это сложная функция с промежуточным аргументом sinj. Дифференцируем ее по формулам

(uⁿ)' = nu^n-1u', (sin u)' = cos u • u':

f(j) = 3 sin²j (sinj)' = 3 sin²j cosj.

Вычислим значение производной при j = p/З:

f(p/3) = 3sin² (p/3) cos(p/3)=3(Ö3/2)² •(1/2)=3•(3/4) • (1/2)=9/8.

Пример 3. Найти производную функции

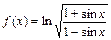
Решение. Сначала преобразуем функцию, используя свойства лога­рифмов: t

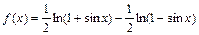
Дифференцируя, получим

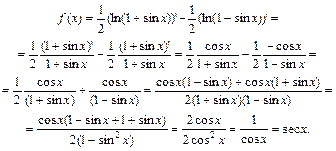
Геометрический смысл производной. Производная функции у =f(x) представляет собой угловой коэффициент касательной, проведенной к графику функции в любой его точке.

Угловой коэффициент касательной, проведенной к графику функции y=f(х) в точке A(а;b), равен значению производной функции при х = а:

k_кас=y'(a)=f'(a).

Уравнение касательной, проведенной к графику функции в этой точке, имеет вид

у— b=k (х -а), где k=f’(a).

Пример 4. Составить уравнение касательной, проведенной к графику функции в точке с абсциссой х=2.

Решение. Сначала найдем ординату точки касания А (2;у). Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кри­вой, т. е.

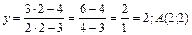
Уравнение касательной, проведенной к кривой в точке А(2;2), имеет вид у - 2 = k(x - 2). Для нахождения углового коэффициента касательной найдем производную:

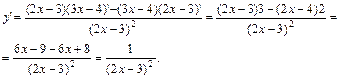
Угловой коэффициент касательной равен значению производной функции при х = 2:

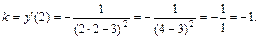
Уравнение касательной таково:

у - 2 = - (х - 2), или у - 2 = -х + 2, т. е. х + у - 4 = 0.

Физический смысл производной. Если тело движется по прямой по за­кону s = s (t), то производная пути s по времени t равна скорости движения тела в данный момент времени t:

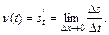
Быстрота протекания физических, химических и других процессов также выражается с помощью производной.

Производная функции у=f(х) равна скорости изменения этой функции при данном значении аргумента х:

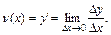
Пример 5. Закон движения точки по прямой задан формулой s=t²+3t+5. В какие моменты времени t скорость движения точки равна нулю?

Решение. Скорость прямолинейного движения точки равна производ­ной пути s по времени t:

v (t) = s' = 3 t² - 6t + 3; v (t) =0,З t² - 6t + 3 = 0,

t² - 2t + 1 = 0, (t — 1)² = 0, откуда t = 1.

Вторая производная. Производной второго порядка (или второй про­изводной) функции называется производная от первой производной у' =f' (х):

у" = (у’)' или f" (х) = (f' (х))'.

Пример 6. Найти вторую производную функции f(x)=tg x.

Решение. Сначала по формуле 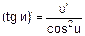найдем первую произ­водную: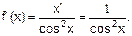

Дифференцируя еще раз по формулам (uⁿ)’=nu^n-1u’, сos u)’=-sin u*u’, найдем вторую производную:

Физический смысл второй производной. Если тело движется прямоли­нейно по закону s=s(t), то вторая производная пути s по времени t равна ускорению движения тела в данный момент времени t:

а (t) = v' = s".

Пример 7. Точка движется по прямой по закону s=t³-5t²+8t+2. (s - в метрах, t - в секундах). Найти ускорение движения точки в конце второй секунды.

Решение. Сначала найдем производную пути s по времени t:

s' = 3 t² - 10 t + 8.

Ускорение прямолинейного движения точки равно второй производной пути s по времени t:

а (t) = s" = 6 t - 10, а(2) = 6 • 2 - 10 = 12 - 10 = 2.

Ускорение движения точки в конце второй секунды равно 2 м/с².

Приложения производной к исследованию функций. Дифференцируе­мая функция у= f (х) возрастает на промежутке ]а, b[, если ее производная положительна в каждой точке этого промежутка.

Дифференцируемая функция у=f(x) убывает на промежутке]а; b[, если ее производная отрицательна в каждой точке этого промежутка.

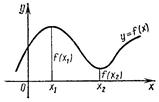
Функция y=f(x) имеет максимум в точке х = x₁ (рис. 38), если для всех значений х, достаточно близких к x₁, выполняется неравенство f(х) < f(х₁); x=х₁ - точка максимума; у_maх =f (х₁) - максимум функции.

Функция у = f(x) имеет минимум в точке х = х₂ (рис. 38), если для всех значений х, достаточно близких к х₂, выполняется неравенство f(x) > f(х₂); х = х₂ - точка минимума; у_maх = f(х₂) - минимум функции.

Точки максимума и минимума называются точками экстремума, а значе­ния функции в этих точках - экстремальными.

Точки, в которых производная функции обращается в нуль, называются критическими, точками I рода.

Первое достаточное условие существования экстре­мума функции. Если при переходе через критическую точку I рода х=х₀ производная функции y=f(х) меняет знак, то х=х₀ - точка

экстремума.

При этом если производная меняет знак с плюса на минус, то х=х₀= - точка максимума, а у_mах =f(х₀). Если же производная меняет знак с минуса на плюс, то х= х₀ - точка минимума, a у_min =f(х₀)

Второе достаточное условие существования экстре­мума функции. Если в точке х = х₀ первая производная функции у=f(x) обращается в нуль, а вторая производная отлична от нуля, то х=х₀ - точка экстремума.

При этом если вторая производная в этой точке положительна (f" (х₀)>0), то х=х₀ - точка минимума; если вторая производная в этой точке отрица­тельна (f"(х₀) < 0), то х= х₀ – точка максимума.

рис. 38.

Направление вогнутости и точки перегиба кривой. Говорят, что на промежутке ]а, b[ кривая обращена выпуклостью вверх или вы­пукла (Ç), если она лежит ниже касательной, проведенной в любой ее точке (рис. 42).

Говорят, что кривая на промежутке ]b,с[ обращена выпуклостью вниз или вогнута (È), если она лежит выше касательной, проведенной в любой ее точке (рис. 42).

Точка А, в которой меняется направление вогнутости кривой, называется точкой перегиба кривой (рис. 42).

График дифференцируемой функции y=f(x) является выпуклым на про­межутке ]а; b[, если вторая производная функции отрицательна в каждой точке этого промежутка.

График дифференцируемой функции y=f(x) является вогнутым на про­межутке ]b; с[, если вторая производная функции положительна в каждой точке этого промежутка.

Точки, в которых вторая производная функции обращается в нуль, назы­ваются критическими точками II рода.

Если при переходе через критическую точку II рода х = х₀ вторая произ­водная функция меняет знак, то х = х₀ - абсцисса точки перегиба. Ордината точки перегиба равна значению

функции в точке х₀, т.е. у_т.п. =f(х₀); А(х₀;f(х₀)) - точка перегиба графика функции у = f(х).

Исследование функций и построение их графиков. Исследование функции можно проводить по следующей схеме:

1. Найти область определения функции.

2. Найти точки пересечения графика функции с осями координат.

3. Найти промежутки монотонности и экстремумы функции.

4. Найти направление вогнутости и точки перегиба графика функции.

5. Для уточнения графика функции рекомендуется найти несколько допол­нительных точек из уравнения функции.

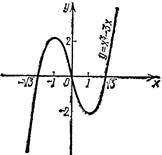
Пример 8. Построить график функции у = х³ - Зх.

Решение 1. Областью определения функции служит множество всех действительных чисел, т. е. х = R.

2. Находим точки пересечения графика функции с осями координат:

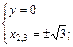
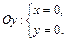
рис.42.	рис. 43.

3. Находим экстремумы функции. Для этого сначала найдем производную у' = Зх² - 3. Затем найдем критические точки I рода: у' = 0,Зх² - 3=0, х² = 1, х₁= 1, х₂ = -1. Отметим эти точки на числовой прямой (рис. 43). Исследуем знак производной в каждом интервале; у'(-2) > 0, у' (0) < 0, у'(2) > 0. Функция возрастает при хÎ] -¥,-1[U]1,+¥[и убывает при хÎ] –1,1[. Итак, х= -1 — точка максимума; у_maх = у(-1)=(-1)³-3(-1)=-1+3=2; х=1 — точка минимума; y_min = у (1) = 1³—3*1=1-3=-2.

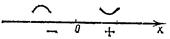
4. Находим направление вогнутости и точки перегиба графика функции. Для этого сначала найдем вторую производную у" = 6х, а затем критические точки II рода: у" =0,6х=0, х = 0. Отметим эту точку на числовой прямой (рис. 44). Исследуем знак второй производной в каждом интервале:

у"(-1) < 0, у"(1)>0.

рис. 44	рис. 45

Таким образом, график является выпуклым при хÎ] -¥,0[ и вогнутым при хÎ] 0, + ¥ [; х = 0 — абсцисса точки перегиба, y_т.п= у(0) = 0; О (0,0) - точка перегиба графика функции.

Отметим все полученные точки в сис­теме координат и соединим их плавной кривой (рис. 45).

Для уточнения графика функции можно найти дополнительные точки, используя уравнение функции: у(-2)= -2, у (2) =2.

Дата добавления: 2014-12-08