Неопределенный интеграл

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Дайте определение функции.

2. Перечислите способы задания функции. Приведите примеры.

3. Сформулируйте определение числовой последовательности.

4. Какие бывают числовые последовательности?

5. Сформулируйте теорему о существовании предела последовательности.

6. Какая существует зависимость, между бесконечной малой и бесконечно большой последовательностями?

7. Дайте определение предела переменной.

8. Напишите уравнение гармонического колебания.

9. Как определяются функции y==arcsin х, y=arccos x,

у= =arctg x, у=arcctg х?

10. Чему равно выражение y=sin(arcsin x)?

11. Как найти приращение аргумента?

12. Как найти приращение функции?

13. Как вычисляется средняя скорость изменения функции?

14. Дайте определение производной функции.

15. Выпишите теоремы о производных алгебраической суммы, произведения, частного.

Понятие неопределенного интеграла. дифференцирование -это действие, с помощью которого по данной функции находится ее производная или диф­ференциал. Например, если F(x) = х¹⁰, то F' (х) = 10х⁹, dF (х) =10x⁹dx.

Интегрирование -это действие, обратное дифференцированию. С помощью интегрирования по данной производной или дифференциалу функции находит­ся сама функция. Например, если F' (х) = 7х⁶, то F (х) == х⁷, так как (х⁷)'=7х⁶.

Дифференцируемая функция F(x), хЄ]a; b[ называется первообразной для функции f (х) на интервале ]а; Ь[, если F' (х) = f (х) для каждого хЄ]a; b[.

Так, для функции f(x) = 1/cos³ х первообразной служит функция F(x)= tg x, поскольку (tg x)'= 1/cos² х.

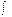Совокупность всех первообразных функций f(x) на интервале ]а; b[ на­зывают неопределенным интегралом от функции f(x) на этом интервале и пишут f (x)dx = F(x) + С. Здесь f(x)dx - подынтегральное выражение;

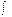f(х)—подынтегральная функция; х—переменная интегрирования: С - про­извольная постоянная.

Например, 5x⁴dx = х⁵ + С, так как (х³ + С)' = 5х⁴.

Приведем основные свойства неопределенного интеграла. 1.Дифференциал неопределенного интеграла равен подынтегральному выражению:

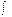d f(x)dx=f(x)dx.

2.Неопределенный интеграл от дифференциала функции равен этой функ­ции, сложенной с произвольной постоянной, т. е.

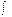dF(x)=F(x)+C.

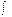
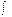3.Постоянный множитель можно выносить за знак неопределенного интеграла:

аf(х)dx = a f(x)dx

4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от каждой функции:

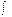
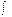
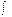(f₁(х) ±f₂(х))dx = f₁(х)dx ± f₂(х)dx.

Основные формулы интегрирования

(табличные интегралы).

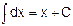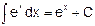1.

2.

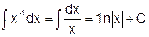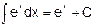3.

4.

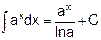5.

6.

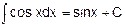7.

8.

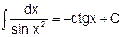9.

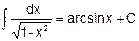10.

11.

Если интеграл затруднительно привести к табличному с помощью элемен­тарных преобразований, то в этом случае пользуются методом подстановки.

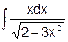Пример 1. Найти

Решение. Произведем подстановку 2 — Зх² = t тогда -6xdx =dt, xdx = -(1/6)dt. Далее, получаем

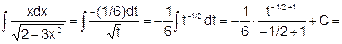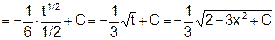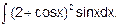Пример 2. Найти

Решение. Сначала положим 2 + cos x = t; тогда -sin xdx= dt, откуда sin xdx = -dt. Далее, получаем

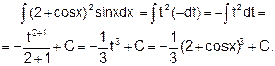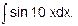Пример 3. Найти

Решение. Положим 10х = t; тогда 10dx = dt, откуда dx=(1/10)dt.

Далее, получаем

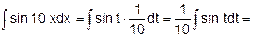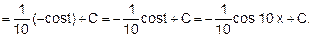В практике интегрирования часто встречаются интегралы, для нахождения которых можно использовать следующие формулы (k = 0, n= 0 — постоянные):

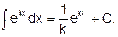1.

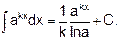2.

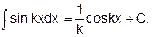3.

4.

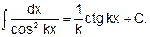5.

6.

7.

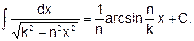8.

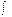
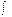Так, при нахождении sinl0xdx можно использовать формулу sinkxdx = - (1/k) cos kx+C, где k=10.

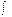Тогда sinl0xdx = -(1/10) сos10х+С.

Дата добавления: 2014-12-08