Функции. Последовательности. Пределы

VI. Элементы вычислительной математики

V. Элементы теории вероятностей и математической статистики.

IV. Обыкновенные дифференциальные уравнения.

Определение обыкновенного дифференциального уравнения. Част­ное и общее решение. Уравнения с разделенными и разделяющимися переменными. Однородные уравнения 1-го порядка, уравнения, приводящиеся к однородным. Уравнения в полных дифференциалах. Линейные уравнения 1-го порядка.

Линейные однородные уравнения высших порядков. Фундамен­тальная система решений.

Опыт. Событие. Виды событий. Случайные события. Виды случайных событий. Относительная частота появления события. Классические определения вероятности. Основные понятия комбина­торики. Операции над событиями. Теоремы сложения и умножения вероятностей.

Противоположные события. Повторные независимые испытания. Формула Бернулли.

Дискретная случайная величина, закон ее распределения. Числовые характеристики распре­деления дискретной случайной величины.

Понятие о законе больших чисел. Понятие об основных задачах математической статистики. Выборочный метод, репрезентативность выборки.

Действия над приближенными числами. Вычисления с заданной точностью, с точным учетом и без точного учета погрешности.

Вычисления на логарифмической линейке и на малых вычисли­тельных машинах. Вычисления с помощью таблиц. Вычисление зна­чений функции по заданной формуле. Решение задач прикладного характера.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Необходимо хорошо усвоить теоремы о пределах:

1. lim (x+y-z)=lim x + lim y – lim z.
2. lim c =c, c-const.
3. lim (xy)=lim x lim y, lim (cx)=c lim x.
4. lim x/y)=lim x / lim y, если lim y =0.
5. lim (x^m)= (lim x)^m.

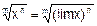Приступим к отысканию пределов функций. Вопрос о пределе функции не имеет смысла, если не указан предел аргумента. Рассмотрим решение примеров.

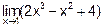Пример 1. Вычислить.

Решение. Применяя теоремы 1, 2, 3, 5, запишем

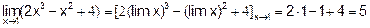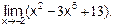Пример 2. Вычислить

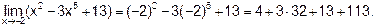Решение

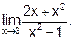Пример 3. Вычислить

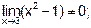Решение

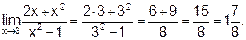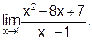Пример 4. Вычислить

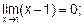Решение. В данном случае теорема о пределе частного не применима, так как Числитель дроби разложим на

множители и сократим дробь на (х -I):

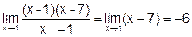Допредельное значение х-1=0, поэтому сокращение на (х -1) законно.

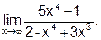Пример 5. Вычислить

Решение. Разделим числитель, и знаменатель дроби на х⁴:

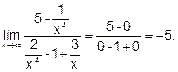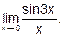Пример 6. Вычислить

Решение. Заменим sin Зх эквивалентной бесконечно ма­лой Зх:

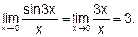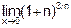Пример 7. Вычислить

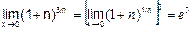Решение.

Дата добавления: 2014-12-08