Определенный интеграл

Вопросы и упражнения для самопроверки

1. Какое действие называется интегрированием?

2. Какая функция называется первообразной для функции f(x)?

3. Дайте определение неопределенного интеграла.

4. Перечислите основные свойства неопределенного интеграла.

5. Каким действием можно проверить интегрирование?

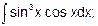
6. Напишите основные формулы интегрирования (табличные интегралы).

7. Найдите интегралы: а) б) в)

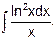г)

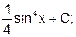Ответы: 7. а) б) в)

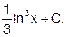г)

Понятие определенного интеграла. Непосредственное вычисление определенного интеграла производится по формуле Ньютона—Лейбница:

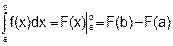где а—нижний предел, Ь—верхний предел, F (x)—какая-нибудь первообразная функции f (х).

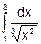Из этой формулы виден порядок вычисления определенного интеграл 1) находят одну из первообразных F (x) данной функции; 2) находят значение F (x) при х = а и х = Ь; 3) вычисляют разность F (Ь) — F (а).

Пример 1. Вычислить интеграл

Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:

Приведем основные свойства определенного интеграла.

1. При перестановке пределов интеграла знак интеграла меняется на противоположный:

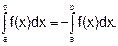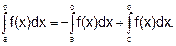2. Отрезок интегрирования можно разбивать на части:

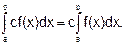3. Постоянный множитель можно выносить за знак интеграла:

4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:

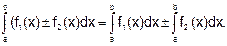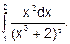Пример 2. Вычислить интеграл

Решение. 1) Произведем подстановку х³+2=t; тогда

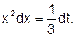3х²dx=dt,

2) Определим пределы интегрирования для переменной t. При х=1 получаем t_н=1³+2=3, при х=2 получаем t_в=2³+2=10.

3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим

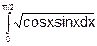Пример 3. Вычислить интеграл

Решение. 1) положим cos х=t; тогда – sinxdx =dt и

sinxdx = -dt. 2) Определим пределы интегрирования для переменной t: t_н=cos0=1:t_в=cos (π/2)=0.

3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим

Пример 4. Вычислить интеграл

Решение. Сначала преобразуем подынтегральное выражение

sin³x = sin² x • sin x = (1 — cos²x) sin x = sin x - cos² x sin x.

Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:

Вычислим каждый интеграл отдельно:

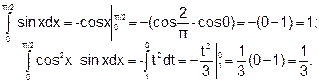cos x =t,

-sin xdx =dt,

sin xdx =-dt,

t_н=cos0 =1

t_в=cos(π/2) =0.

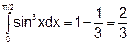
Тогда

Приложения определенного интеграла. Площадь плоской фигуры. Площадь криволинейной трапеции аАВЬ (рис. 46), ограниченной гpaфикoм непрерывной функции y=f(x), где

хЄ[а, b], отрезком [a,b] оси Ох, отрезками прямых х =a и х = b, вычисляется по формуле

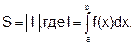(1)

Пример 5. Вычислить площадь фигуры, ограниченной параболой у = х² , прямыми х = - 1, х = 2 и осью абсцисс (рис.47).

Решение. Применяя формулу (1), получаем

т.е. S=3 кв. ед.

Площадь фигуры ABCD (рис. 48), ограниченной графиками непрерывных функций у =f₁(x) и у f₂= (x), где х Є[а, b], отрезками прямых х = а и х = Ь, вычисляется по формуле

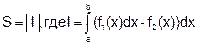(2)

		рис. 47

Пример 6. Вычислить площадь фигуры, ограниченной осью Ох и линией у = х² — 2х (рис. 49).

Решение. Найдем пределы интегрирования, т. е. абсциссы точек пере­сечения графиков функций y=х²—2х и у=0 (ось Ох). Для этого решим систему

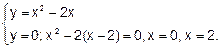Теперь найдем искомую площадь:

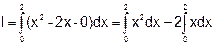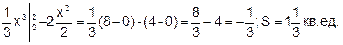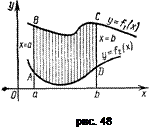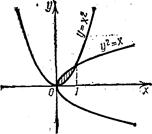
Пример 7. Вычислить площадь фигуры, ограниченной линиями у = х² и у² =х (рис. 50).

Решение. Найдем пределы интегрирования, т. е. абсциссы точек пере­сечения графиков функций у = х² и у² =х. Для этого решим систему

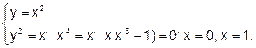Искомую площадь вычисляем по формуле (2) при f₁(x)=x²,

рис. 50

рис. 51

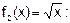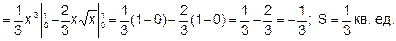Объем тела вращения. Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции аАВЬ, ограниченной непрерывной кривой у = f (x), где x Є [а, b], отрезком [а, Ь] оси Ох, отрезками прямых х = а и х = b (рис. 51), вычисляется по формуле

(3)

Пример 8. Вычислить объем тела, образованного вращением вокруг ocи Ох фигуры, ограниченной параболой у²=2х, прямой х = 3 и осью Ох (рис. 52).

Решение. Применяя формулу (3), находим искомый объем:

(куб. ед.)

Объем тела, образованного вращением вокруг оси Оу криволинейной трапеции аАВЬ, ограниченной непрерывной кривой x=f(y), где у Є [а, b], отрезком [а, b] оси Оу, отрезками прямых у = а и у = Ь (рис. 53), вычисляется по формуле

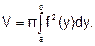(4)

Пример 9. Вычислить объем тела, образованного вращением вокруг ocи Оу фигуры, ограниченной параболой у=х² и прямой у = 4 (рис. 54).

Решение. Применяя формулу (4), находим искомый объем:

(куб. ед.)

Путь, пройденный точкой. Если точка движется прямолинейно и ее скорость v=f(t) есть известная функция времени t, то путь пройден­ный точкой за промежуток времени [t₁,t₂], вычисляется по формуле

(5)

Дата добавления: 2014-12-08