Вопросы для самопроверки. 1. Дайте определение производной функции

1. Дайте определение производной функции.

2. В чем состоит геометрический смысл производной?

3. В чем состоит физический смысл производной?

4. Дайте определение второй производной функции.

5. В чем состоит физический смысл второй производной?

6. Напишите все формулы дифференцирования.

7. Как найти промежутки возрастания и убывания функции?

8. Как найти точки экстремума и экстремумы функции?

9. Как найти промежутки выпуклости и вогнутости кривой?

10. Как найти точки перегиба кривой?

11. Найдите производные функций: а) у = In tg (х/2);

б) у = cos² Öx; в) f(x)=(x+1)2х-1.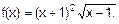

12. Составьте уравнение касательной к кривой у = х² — 4х в точке с абсциссой х = 1.

13. Прямолинейное движение точки задано уравнением

(s - в метрах, t - в секундах). Найдите скорость и ускорение движения точки в конце второй секунды,

14. Какой из прямоугольников с периметром, равным 48см, имеет наибольшую площадь?

15. Число 66 представьте в виде суммы двух положительных слагаемых так, чтобы произведение этих чисел было наибольшим.

Ответы. 11. a) cosec х; б) 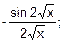в)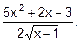

12. 2х+у+1=0. 13. 3 м/с, 2 м/с². 14. Квадрат со стороной 12 см. 15. 33 и 33.

Решение. Находим производную данной функции, используя формулы

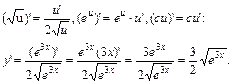
Умножив производную на дифференциал аргумента, получим дифференциал: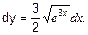

Пример 2. Вычислить значение дифференциала функции n = In sin 2j при j = p/8, Dj = 0,02.

Решение: Дифференциал функции вычисляем по формуле dv = v' (j) dj.

Прежде чем применить эту формулу, используя равенства

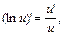(sin u)’ = cos u ^, u ’, (си)’= си ’, находим производную функции и ее значение при j = p/8:

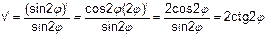
Понятие о дифференциальном уравнении. Дифференциальным уравне­нием называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции).

Если дифференциальное уравнение содержит производную или дифферен­циал не выше первого порядка, то оно называется дифференциальным урав­нением первого порядка. Общий вид такого уравнения F (х, у, у') = 0.

Общим решением дифференциального уравнения первого порядка назы­вается функция у = j(х, С) от х и произвольной постоянной С, обращающая это уравнение в тождество.

Общее решение, записанное в неявном виде Ф (х, у. С) =0, называется общим интегралом.

Частным решением уравнения F (х, у, у') = 0 называется решение, полу­ченное из общего решения при фиксированном значении С: у =j(х, С_о), где С_о - фиксированное число.

Частным интегралом уравнения F(x, у, у') = 0 называется интеграл, полученный из общего интеграла при фиксированном значении С: Ф (х, у, С_о) = 0.

График любого частного решения дифференциального уравнения F (х, у, у') = 0 называется интегральной кривой. Общему решению (и общему ин­тегралу) этого уравнения соответствует семейство интегральных кривых, зави­сящих от одного параметра С.

Пример 1. Составить уравнение кривой y=f(x), если угловой коэффи­циент касательной, проведенной в любой точке кривой, равен 2х.

Решение. Так как на основании геометрического смысла производной у' = k_кас, то получим дифференциальное уравнение первого порядка:

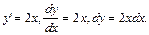
Чтобы найти, искомую функцию у=f(х), надо проинтегрировать обе час­ти уравнения: òdy = ò 2xdx. Отсюда получим общее решение дифференциаль­ного уравнения:

у=х²+С. Геометрически это решение представляет собой семейство парабол (рис. 55) с вершиной на оси Оу, симметричных относитель­но этой оси.

Чтобы из общего решения выделить частное решение, надо задать началь­ные условия. Пусть у = -1 при х=1; тогда общее решение примет вид -1 = 1 + С, откуда С = - 2. Геометрически частное решение у = х² - 2 представляет со­бой параболу, проходящую через точку (1; -1) (рис. 55).

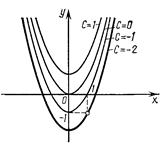
рис. 55

Дифференциальные уравнения с раз­деляющимися переменными. Общий вид такого уравнения

Х (х) • Y (y)dx + X₁(x) • Y₁ (у) • dy = 0,

где Х (х), Х₁(х) — функции только от х, Y(у), Y₁(у)—функции только от у.

Поделив обе части уравнения на произве­дение X₁(x)•Y(у)¹0, получим уравнение с разделенными переменными:

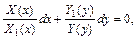
Дата добавления: 2014-12-08