Метод интегрирования по частям

Пусть 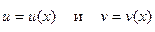- непрерывно дифференцируемые функции.

Тогда справедлива формула:

.

Эта формула называется формулой интегрирования по частям.

В интегралах типа 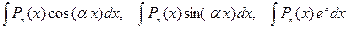, где , полагаем функцию u(x)=P_n(х), а оставшуюся часть подынтегрального выражения берем за dv и находим функцию v.

Если подынтегральное выражение содержит функции ln x, arccos x, arcsin x,

arctg x, arcctg x, то именно эти функции берем за функцию u. Иногда до применения формулы интегрирования по частям необходимо сделать замену переменной.

Пример 3. Вычислить интеграл .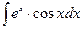

Решение: Положим .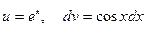

Тогда 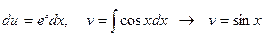(одна из первообразных);

имеем (*).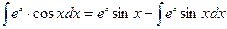

Интеграл снова вычисляем по частям, положив 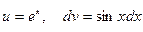. Тогда .

Подставляя значение полученного интеграла в (*) находим

.

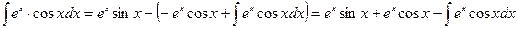Перенося интеграл из правой части равенства в левую, получаем ,

откуда окончательно имеем

Дата добавления: 2014-12-08