Основные теоретические сведения. Изучение динамики вращательного движения твердых тел

Изучение динамики вращательного движения твердых тел

Лабораторная работа № 4

Цель работы: опытным путем проверить справедливость основного закона динамики вращательного движения твердых тел.

Оборудование: автоматизированная установка «Маятник Обербека», линейка с миллиметровыми делениями.

Основной задачей механики является определение положения тела в пространстве и во времени. Решению этой задачи способствует ряд физических законов, одним из которых является основной закон динамики вращательного движения абсолютно твердого тела. Абсолютно твердым телом называется тело, деформациями (изменением формы и размеров) которого в условиях данной задачи можно пренебречь. В большинстве случаев реальные тела можно с достаточной для практики точностью считать абсолютно твердыми. В дальнейшем мы их будем называть просто твердыми телами.

Основной закон динамики (II закон Ньютона) для вращательного движения твердого тела: в инерциальной системе отсчета угловое ускорение 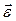, приобретаемое телом, вращающимся относительно неподвижной оси, прямо пропорционально суммарному моменту 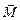внешних сил, действующих на тело, и обратно пропорционально моменту инерции 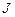относительно данной оси:

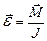, (1)

где 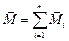– сумма моментов всех приложенных к телу внешних сил относительно оси вращения.

Моментом силы относительно неподвижной оси называется физическая величина, равная векторному произведению радиуса-вектора 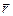, проведенного от оси в точку приложения силы, на силу :

,

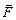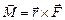где 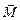– псевдовектор, то есть вектор, не имеющий определенной точки приложения. Он направлен всегда вдоль оси вращения в соответствии с правилом правого винта (буравчика): при вращении правого винта от 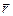к 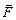его поступательное движение укажет направление 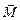(рис. 1).

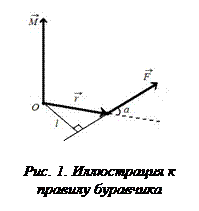Модуль момента силы:

,

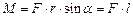где 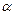– угол между 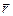и ;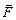

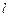– плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).

Единица измерения момента силы в СИ:

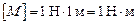(ньютон-метр).

Моментом инерции системы (тела) относительно оси вращения называется скалярная физическая величина, равная сумме произведения масс 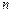материальных точек системы на квадраты их расстояний до рассматриваемой оси:

.

В случае непрерывного распределения масс эта сумма сводится к интегралу:

,

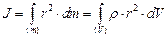где 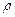– плотность тела;

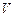– объем тела;

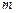– масса тела;

– расстояние от оси вращения.

Единица измерения момента инерции в СИ:

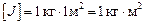(килограмм-квадратный метр).

Момент инерции легко рассчитать только в случае тела однородного по плотности и симметричного относительно оси, проходящей через центр масс (воображаемая точка, в которой можно считать сосредоточенной всю массу системы, называемая также центром инерции). Момент инерции тела относительно произвольной оси можно вычислить, используя теорему Штейнера: момент инерции тела 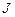относительно любой произвольной оси равен сумме момента инерции 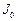относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела 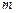на квадрат расстояния между осями :

.

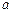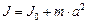Момент инерции тел неправильной геометрической формы проще определить экспериментально, чем рассчитать.

Дата добавления: 2014-12-08