Обоснование метода. Получим рабочие формулы для проверки основного закона динамики вращательного движения твердого тела

Получим рабочие формулы для проверки основного закона динамики вращательного движения твердого тела.

Модуль углового ускорения маятника связан с модулем линейного ускорения точек на ободе шкива радиуса 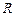соотношением . Так как нить нерастяжима, то ускорение 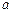равно ускорению платформы. С учётом того, что путь, проходимый телом из состояния покоя при равнопеременном движении равен , где – время движения, получаем:

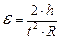. (2)

Найдём суммарный момент сил, действующих на маятник. К нему приложены сила тяжести и сила натяжения нити. Чтобы упростить задачу, маятник устанавливают в безразличное равновесие, тогда центр тяжести будет лежать на оси маятника и момент силы тяжести будет равен нулю.

Таким образом, суммарный момент сил, действующих на маятник, будет определяться только моментом силы натяжения нити.

Считая нить и блок невесомыми и пренебрегая силами трения в блоке, силу натяжения можно считать одинаковой по всей длине нити.

Найдем эту силу. На платформу массы 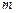действует сила натяжения нити и сила тяжести (рис. 2). Согласно второму закону Ньютона векторная сумма этих сил равна произведению массы платформы на её линейное ускорение:

.

Проецируя это уравнение на ось , получаем , т. е. .

Так как , получаем .

Таким образом, момент силы натяжения, то есть суммарный момент сил, действующих на маятник:

. (3)

Получим выражение для момента инерции маятника.

Пусть 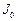– момент инерции маятника без грузов, – момент инерции одного груза массы 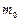относительно оси, проходящей через его центр масс. Согласно теореме Штейнера момент инерции этого груза относительно оси вращения маятника будет , где 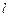– расстояние между осью вращения и центром тяжести груза. Следовательно, момент инерции маятника с грузами:

. (4)

Исследование зависимости при и , при позволяет сделать вывод о справедливости основного закона динамики вращательного движения.

Дата добавления: 2014-12-08