
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дії над матрицями
|
|
|
|
Додавання. Дія додавання матриць вводиться тільки для матриць однакових розмірів.
Сумою двох матриць 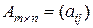 і
і  називається матриця
називається матриця  така, що
така, що 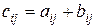 , де
, де 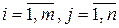 .
.
Сума трьох матриць 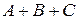 – це матриця, яка отримується послідовним додаванням даних матриць, тобто
– це матриця, яка отримується послідовним додаванням даних матриць, тобто 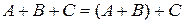 .
.
Аналогічно визначається 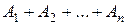 для
для  .
.
Приклад 1.1. Знайти суму  , якщо
, якщо
 .
.
Розв’язок.
 . t
. t
Множення матриці на число. Добутком матриці 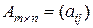 на число
на число  (або числа
(або числа  на матрицю
на матрицю  ) називається матриця
) називається матриця  така, що
така, що  .
.
Добуток матриці 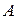 на число
на число  позначається
позначається  або
або  .
.
Приклад 1.2. Знайти добуток матриці

на число  .
.
Розв’язок.
 . t
. t
Матриця  називається протилежною до матриці
називається протилежною до матриці 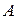 .
.
Різницю матриць  можна визначити як
можна визначити як  .
.
Операції додавання матриць і множення матриці на число називають лінійними операціями над матрицями імають наступні властивості:
1. 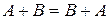 ;
;
2.  ;
;
3.  ;
;
4. 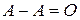 ;
;
5.  ;
;
6.  ;
;
7.  ;
;
8. 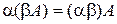 ,
,
де А, В, С, О – матриці,  – числа.
– числа.
Множення матриць. Операція множення двох матриць вводиться тільки для випадку, коли число стовпців першої матриці рівне числу рядків другої матриці. Такі матриці називаються узгодженими.
Добутком матриці 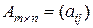 на матрицю
на матрицю 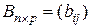 називається матриця
називається матриця  така, що
така, що 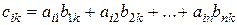 , де
, де 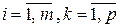 , тобто елемент і -го рядка і
, тобто елемент і -го рядка і  - го стовпчика матриці
- го стовпчика матриці 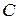 дорівнює сумі добутків елементів і -го рядка матриці
дорівнює сумі добутків елементів і -го рядка матриці 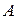 на відповідні елементи
на відповідні елементи  - го стовпчика матриці
- го стовпчика матриці 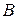 .
.
Приклад 1.3. Знайти добуток 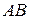 , якщо
, якщо
 .
.
Розв’язок.

 . t
. t
Якщо А і В квадратні матриці одного порядку, то добутки АВ і ВА завжди існують. Якщо 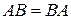 , то матриці А і В називаються перестановочними.
, то матриці А і В називаються перестановочними.
Якщо матриця 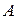 узгоджена з матрицею
узгоджена з матрицею 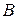 , а матриця
, а матриця 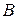 узгоджена з матрицею
узгоджена з матрицею 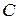 , то під добутком
, то під добутком 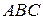 трьох матриць розуміємо матрицю, отриману послідовним множенням даних матриць, тобто –
трьох матриць розуміємо матрицю, отриману послідовним множенням даних матриць, тобто – 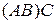 .
.
Операція множення матриць має властивості:
1.  ;
;
2.  ;
;
3.  ;
;
4. 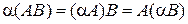 ;
;
5. 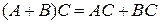 ;
;
6.  ,
,
де А, В, С – матриці,  – одинична та нульова матриці відповідно,
– одинична та нульова матриці відповідно,  – число.
– число.
Елементарні перетворення матриць. Елементарними перетвореннями матриць є наступні перетворення:
1) множення деякого рядка або стовпця матриці на число відмінне від нуля;
2) додавання до одного рядка або стовпця матриці іншого рядка або стовпця, помноженого на довільне число;
3) перестановка місцями двох рядків або стовпців матриці.
Дві матриці 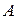 і
і 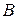 називаються еквівалентними, якщо одна з них отримується з іншої за допомогою елементарних перетворень і позначаються
називаються еквівалентними, якщо одна з них отримується з іншої за допомогою елементарних перетворень і позначаються 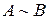 .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 837; Нарушение авторских прав?; Мы поможем в написании вашей работы!