Властивості визначників

Основні поняття

ВИЗНАЧНИКИ

Лекція 2

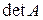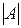Квадратній матриці А порядку п можна поставити у відповідність число, яке називається її визначником або детермінантом і позначається або , або 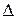та обчислюється наступним чином:

1. , :

.

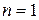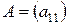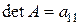2. , :

.

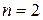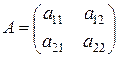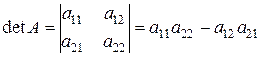3. , :

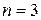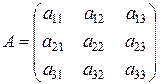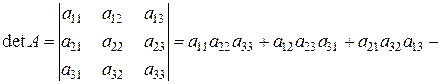
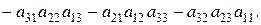
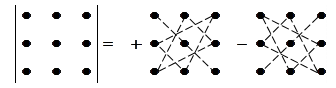Для обчислення визначника 3-го порядку зручно користуватися правилом трикутників, яке можна зобразити схематично:

Правило обчислення визначника для матриці порядку 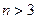єдосить складним для сприйняття і застосування. Проте відомі методи, що дають можливість обчислити визначники високих порядків на основі визначників низьких порядків. Деякі з них розглянемо далі.

Приклад 2.1. Обчислити визначник матриці

.

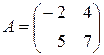Розв’язок.

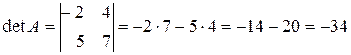. t

Приклад 2.2. Обчислити визначник матриці

.

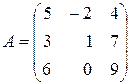Розв’язок.

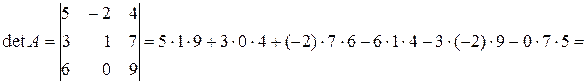
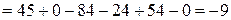. t

Сформулюємо основні властивості визначників, які справедливі для визначників всіх порядків. Деякі з них пояснимо на визначниках 3-го порядку.

1. Визначник матриці, транспонованої до даної, рівний визначнику даної матриці:

Дійсно,

.

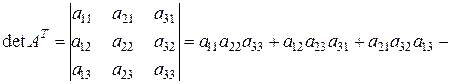
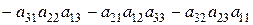
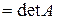2. Якщо всі елементи деякого рядка (стовпчика) рівні нулю, то визначник рівний нулю:

Дійсно,

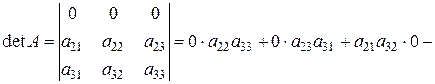
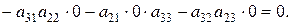
3. Якщо елементи деякого рядка (стовпчика) визначника мають спільний множник, то його можна винести за знак визначника:

.

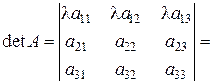
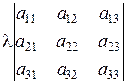4. При перестановці двох рядків (стовпчиків) визначник міняє знак:

.

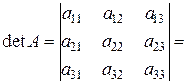
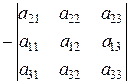5. Якщо визначник має два однакові рядки (стовпчики), то він рівний нулю.

Дійсно, міняючи місцями однакові рядки (стовпчики ) і враховуючи властивість 4, отримаємо .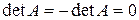

6. Якщо визначник має два пропорційні рядки (стовпчики), то він рівний нулю.

Дійсно, якщо винести коефіцієнт пропорційності 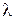за знак визначника, то отримаємо визначник з двома однаковими рядками (стовпчиками ).

7. Визначник, у якого кожний елемент деякого рядка (стовпчика) є сумою двох доданків, рівний сумі двох визначників, у першого з яких у вказаному рядку (стовпчику) стоять перші доданки, а в другому – другі доданки, інші рядки (стовпчики) у всіх визначників однакові:

.

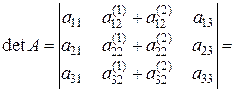
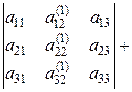
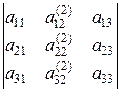8. Якщо матриця В отримана з матриці А додаванням до деякого рядка (стовпчика) іншого рядка (стовпчика), помноженого на числ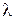о , то .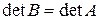

Ця властивість випливає з властивостей 6, 7.

Подальші властивості визначників пов’язані з поняттями мінору та алгебраїчного доповнення.

Мінором елемента 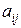матриці 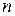-го порядку називається визначник п-1 -го порядку, отриманий з початкового шляхом викреслювання -го рядка і 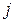-го стовпчика (на перетині яких знаходиться вибраний елемент). Позначається .

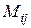Так, наприклад, якщ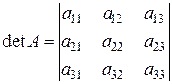о , то

; .

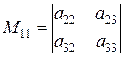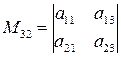Алгебраїчним доповненням елемента 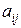квадратноїматриці називається число

,

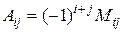тобто його мінор, взятий із знаком 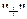, якщо сума 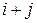– парне число, та із знаком 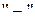, якщо сума 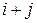непарна.

Так, наприклад, , .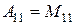

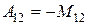9. Розклад визначника за елементами деякого рядка або стовпчика. Визначник дорівнює сумі добутків елементів деякого рядка (стовпчика) на алгебраїчні доповнення цих елементів:

…+ ,

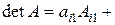
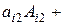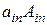де і – номер фіксованого рядка, 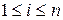, або

…+ ,

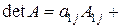
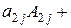де 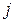– номер фіксованого стовпчика, .

Проілюструємо і доведемо властивість 9 на прикладі визначника 3-го порядку. Так розклад за елементами 1-го рядка має вигляд

=

.

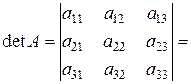
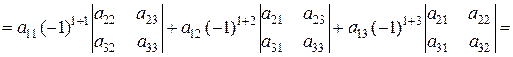
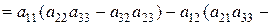
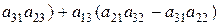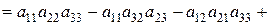
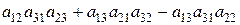
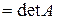10. С ума добутків елементів деякого рядка (стовпчика) на алгебраїчні доповнення відповідних елементів іншого рядка (стовпчика) рівна нулю.

Так, наприклад, якщ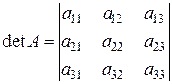о , то

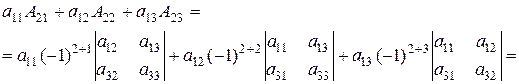
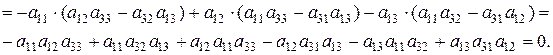
11. Визначник трикутної матриці (або визначник трикутного вигляду) дорівнює добутку елементів її головної діагоналі:

.

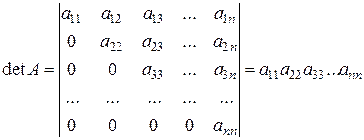Дійсно, розкладаючи визначник за елементами 1-го стовпчика, отримаємо

.

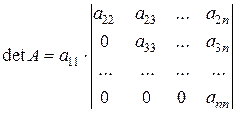Отриманий визначник знову розкладемо за елементами 1-го стовпчика:

.

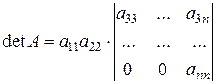Продовжуючи цей процес, отримаємо .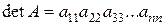

Аналогічно можна показати, що

.

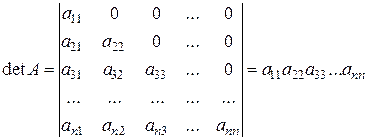Властивість 9 – розклад визначника за елементами деякого рядка або стовпчика – дозволяє звести обчислення визначників 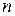- го порядку до обчислення 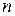визначників 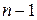-го порядку.

Використовуючи властивості визначників, можна перетворити визначник 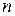- го порядку так, щоб всі елементи деякого рядка або стовпця, крім можливо одного, дорівнювали нулю. Таким чином, обчислення визначника 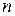- го порядку, якщо він відмінний від нуля, зводиться до обчислення визначника 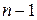-го порядку.

Приклад 2.3. Обчислити визначник матриці

,

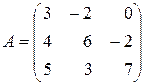розклавши його за елементами деякого рядка або стовпчика.

Розв’язок. Для розкладу визначника зазвичай вибирають той рядок або стовпчик, де є нульові елементи, так як відповідні їм доданки в розкладі будуть рівні нулю, тому розкладемо визначник за елементами 1-го рядка:

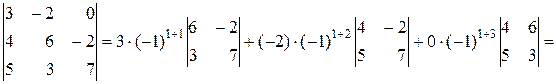
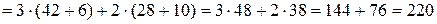. t

Приклад 2.4. Обчислити визначник матриці

,

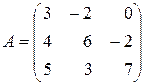використовуючи властивості визначників.

Розв’язок. Приведемо визначник до трикутного вигляду:

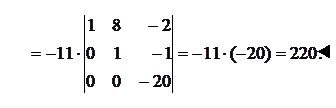
Теоретичні питання

2.1. Що називається визначником матриці 1-го порядку?

2.2. Що називається визначником матриці 2-го порядку?

2.3. Що називається визначником матриці 3-го порядку?

2.4. Які основні властивості визначників?

2.5. Що називається мінором елемента 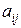матриці 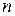-го порядку?

2.6. Що називається алгебраїчним доповненням елемента 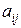матриці 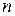-го порядку?

2.7. Які є методи обчислення визначників 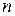-го порядку?

Задачі та вправи

2.1. Обчислити визначники:

а) 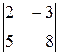; б) .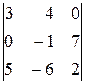

2.2. Обчислити визначники, використовуючи властивості визначників:

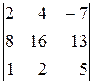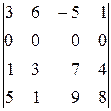а) ; б) ; в) .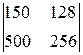

2.3. Знайти алгебраїчні доповнення елементів 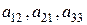матриці

.

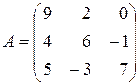2.4. Обчислити визначник

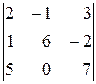
трьома способами:

а) за означенням (правило трикутника);

б) розклавши за елементами рядка або стовпчика;

в) звівши за допомогою властивостей до трикутного вигляду.

2.5. Обчислити визначник:

.

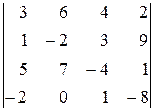Розв’язок. Використовуючи властивості визначників, зведемо обчислення визначника 4 -го порядку до обчислення визначника 3-го порядку:

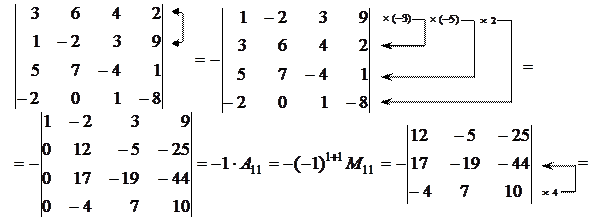
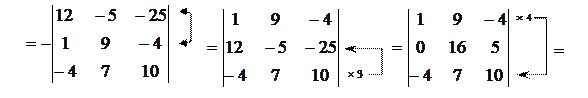
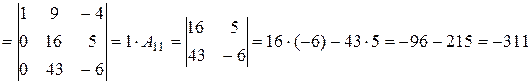. t

Дата добавления: 2014-11-29