
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лінійні операції над векторами в координатній формі
|
|
|
|
Нехай заданий базис  і вектори
і вектори 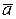 (
( ,
,  ,
, 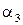 ),
), 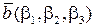 або, що те ж саме,
або, що те ж саме, 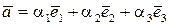 ,
, 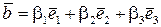 .
.
Сума векторів. Запишемо суму векторів
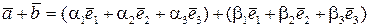
або, згідно властивостям лінійних операцій над векторами,
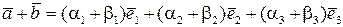 . (5.3)
. (5.3)
Таким чином, при додаванні векторів їх відповідні координати додаються.
Добуток вектора на число. Помножимо вектор 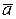 на число
на число 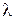 :
:

або
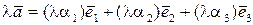 . (5.4)
. (5.4)
Тобто при множенні вектора на число координати вектора множаться на це число.
Приклад 5.1. В базисі  дано вектори
дано вектори 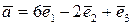 ,
,  . Знайти вектор
. Знайти вектор  .
.
Розв’язок. Згідно формулам (5.3), (5.4)
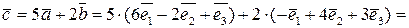
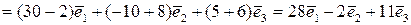 .
.
Відповідь: 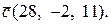 t
t
Рівність векторів. З означення вектора як направленого відрізка, який можна переміщати в просторі паралельно самому собі, випливає, що два вектори 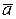 і
і 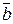 рівні тоді і тільки тоді, коли рівні їх координати:
рівні тоді і тільки тоді, коли рівні їх координати:

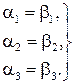
Колінеарність векторів. Вияснимо умови колінеарності векторів 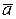 і
і 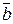 ,заданих своїми координатами.
,заданих своїми координатами.
Так як 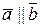 , то за властивостями добутку вектора на число можна записати
, то за властивостями добутку вектора на число можна записати 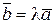 , де
, де 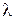 – деяке число, тобто
– деяке число, тобто
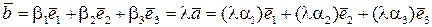 .
.
Звідси 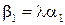 ,
, 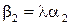 ,
, 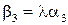 , тобто
, тобто  ,
, 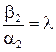 ,
, 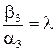 або
або
 . (5.5)
. (5.5)
Таким чином, координати колінеарних векторів пропорційні. Справедливе і обернене твердження: вектори, що мають пропорційні координати, колінеарні.
Зауваження. Співвідношення (5.5) умовно записуватимемо і у випадку, коли серед чисел 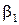 ,
, 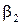 ,
,  є рівні нулю.
є рівні нулю.
Нехай на площині заданий базис 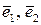 і вектори
і вектори 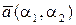 ,
, 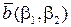 . В цьому випадку мають місце формули, аналогічні формулам (5.3) – (5.5).
. В цьому випадку мають місце формули, аналогічні формулам (5.3) – (5.5).
Приклад 5.2. Перевірити, чи колінеарні вектори 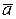 і
і 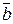 , задані в базисі
, задані в базисі  :
:
а) 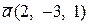 ,
, 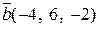 ; б)
; б) 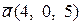 ,
, 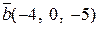 .
.
Розв’язок. Згідно формули (5.5):
а) 
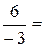
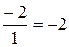 , а отже
, а отже 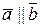 .
.
б) 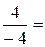
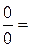
 .
.
Так як друга координата в обох векторів рівна нулю, то їх можна розглядати як вектори, задані на площині в базисі 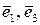 , а отже
, а отже 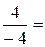
 і
і 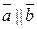 . t
. t
Приклад 5.3. В базисі 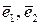 дано вектори
дано вектори 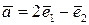 ,
, 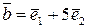 . Показати, що вектори
. Показати, що вектори 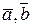 утворюють базис, і знайти координати вектора
утворюють базис, і знайти координати вектора  в базисі
в базисі  .
.
Розв’язок. Якщо два вектори утворюють базис, то вони неколінеарні. Згідно формули (5.5):
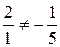 ,
,
а отже вектори  неколінеарні і утворюють базис.
неколінеарні і утворюють базис.
В новому базисі  вектор
вектор  можна представити у вигляді лінійної комбінації
можна представити у вигляді лінійної комбінації
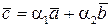 ,
,
де коефіцієнти  ,
, 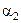 – невідомі і є координатами вектора
– невідомі і є координатами вектора  в базисі
в базисі  .
.
Знайдемо ці координати. Для цього розпишемо розклад вектора  в координатній формі:
в координатній формі:
 ,
,
що рівносильно системі двох лінійних рівнянь з двома невідомими
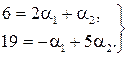
Розв’яжемо цю систему за формулами Крамера:
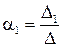 ;
; 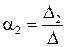 .
.
Обчислимо визначники:
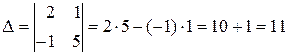 ;
;
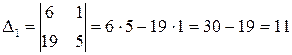 ;
;
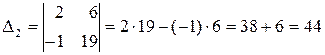 .
.
Отримаємо 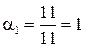 ;
;  .
.
Відповідь:  . t
. t
Приклад 5.4. В базисі  дано вектори
дано вектори  ,
, 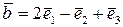 ,
, 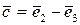 . Показати, що вектори
. Показати, що вектори 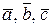 утворюють базис, і знайти координати вектора
утворюють базис, і знайти координати вектора 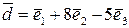 в базисі
в базисі 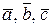 .
.
Розв’язок. Якщо три вектори утворюють базис, то жоден з них не є лінійною комбінацією двох інших. Тоді визначник, складений з координат цих векторів, відмінний від нуля, так як лінійні операції над векторами зводяться до відповідних лінійних операцій над їх координатами. Обчислимо цей визначник:
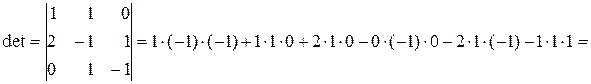
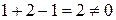 .
.
Отже, вектори 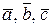 утворюють базис.
утворюють базис.
В новому базисі 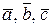 вектор
вектор  можна представити у вигляді лінійної комбінації
можна представити у вигляді лінійної комбінації
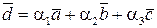 ,
,
де коефіцієнти  – невідомі і є координатами вектора
– невідомі і є координатами вектора  в базисі
в базисі 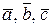 .
.
Знайдемо ці координати. Для цього розпишемо розклад вектора  в координатній формі:
в координатній формі:
 ,
,
що рівносильно системі трьох лінійних рівнянь з трьома невідомими

Розв’яжемо цю систему за формулами Крамера:
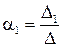 ;
; 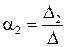 ;
; 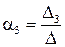 .
.
Очевидно, що визначник 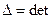 як визначник транспонованої матриці:
як визначник транспонованої матриці:
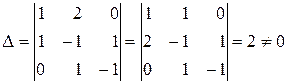 .
.
Обчислимо
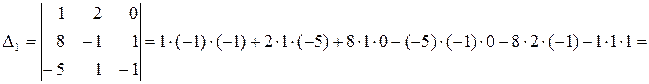

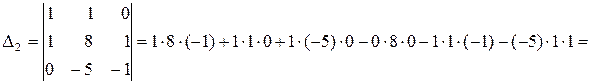
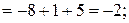
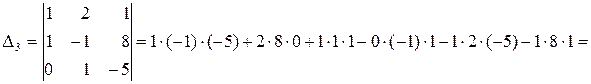
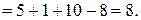
Отримаємо  ;
;  ;
; 
Відповідь: 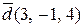 . t
. t
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1047; Нарушение авторских прав?; Мы поможем в написании вашей работы!