Основные теоретические сведения. Указания к выполнению работы

Содержание и порядок выполнения работы

ЗАВИСИМОСТЕЙ

ИССЛЕДОВАНИЕ КОРРЕЛЯЦИОННЫХ

Цель работы – исследование корреляционных зависимостей между случайными величинами, расчет коэффициента корреляции, проверка гипотезы о некоррелированности случайных величин.

Перед выполнением работы необходимо самостоятельно изучить раздел 2.11 [2].

1. Снять выборку из N наблюдений в виде 20 пар чисел (x_J; y_J) с графиков на рисунках по выбранному варианту задания.

2. Из таблицы случайных чисел выписать блок случайных чисел J ℓ, где J – номер строки, а ℓ - номер столбца случайных чисел.

Принять J=1,2,…., N; ℓ =1.2,…., n=3 или 5.

3. Провести имитационный эксперимент с одной из случайных величин пары (x_J; y_J) - y_J для получения ее дублированных значений у_J1, у_{J 2},…., у_{J ℓ}. Принять относительную погрешность в эксперименте ε=0,01.

4. Определить среднее значение , составить таблицу пар (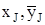) случайных величин.

5. Нанести на график точки, соответствующие результатам эксперимента. Провести качественный анализ поля корреляции.

6.Проверить гипотезу о некоррелированности случайных величин: рассчитать выборочный коэффициент корреляции r, определить расчетное и табличное значения t-критерия Стьюдента; проверить условие некоррелированности величин t_расч£ t_табл . Провести количественный анализ поля корреляции.

4.2.1. Основные теоретические сведения

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой. В этом случае статистическую зависимость называют корреляционной. Среднее арифметическое значение Y, соответствующих значению X=x, называют условным средним .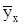

Корреляционной зависимостью Y от X называют функциональную зависимость условной средней 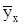от x:

. (4.1)

Уравнение (4.1) называют уравнением регрессии Y на X; функцию f(x) называют регрессией Y на X, а ее график – линией регрессии Y на X.

Чем больше корреляционная связь соответствует функциональной связи, тем более тесной она считается. Наличие типа связи устанавливается в результате проведения корреляционного анализа. В процессе корреляционного анализа формируются следующие заключения: о наличии или отсутствии зависимости между 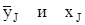; о характере зависимости (функциональная, корреляционная); типе зависимости (линейная, нелинейная, параболическая, экспоненциальная и пр.); знаке связи (положительная, отрицательная); силе связи (тесная, слабо выраженная и др.).

Корреляционный анализ проводят двумя методами: анализом поля корреляции и анализом выборочного коэффициента корреляции.

Полем корреляции называют рисунок, выполненный в прямоугольной системе координат y, x, на котором наносят точки y_xJ и x_J. Анализ поля корреляции проводится визуально.

Более точным является метод анализа выборочного коэффициента корреляции, основанного на математических расчетах и постулатах. Рассмотрим случай корреляции между двумя случайными величинами y и x. Присвоим каждой точке на поле корреляции свой номер J. Такой же номер будет у взаимосвязанной пары координат этой точки. Обозначим через N общее число точек с координатами y_J и x_J. Оценка линейной статистической связи между случайными величинами y и x характеризует коэффициент парной корреляции r, определяемой по формуле [4]

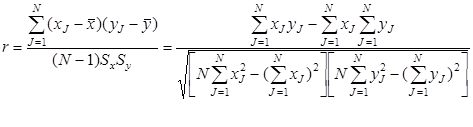, (4.2)

где J – номер наблюдения (опыта), J=1,2,….,N;

N – объем выборки парных точек (y_J, x_J);

y_J, x_J – результаты измерений значений случайных величин соответственно x и y;

S_x, S_y – выборочные стандарты случайных величин соответственно x и y.

Выборочный коэффициент корреляции имеет следующие свойства: 1r 1£1; величина r не изменяется при изменении начала отсчета величин и масштаба измерения x и y; в величине r одновременно заложена доля случайности и нелинейности связи между x и y.

При отрицательном r с увеличением одной из величин другая в среднем будет убывать (отрицательная связь). Чем ближе коэффициент корреляции к +1 или –1, тем выше степень линейной зависимости между случайными величинами. Если r=0, то говорят, что линейная статистическая зависимость между случайными величинами отсутствует. Однако выводы корреляционного анализа можно делать только после доказательств равенства или отличия от нуля рассчитанного значения r методами математической статистики.

Для оценки "значимости" или ²незначимости² (r=0) коэффициента r используют t-распределение Стьюдента. Процедура:

а) определяют расчетное значение t-критерия Стьюдента t_расч по формуле [4]

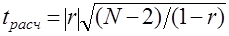. (4.3)

б) по табл. П.3 Приложения определяют табличное значение t-критерия Стьюдента, при выбранном уровне значимости и числе степеней свободы f=N-2;

в) проводят сравнение табличного и расчетного значения критерия, если t_расч<t_табл. принимают гипотезу о некоррелированности случайных величин. В противном случае, когда t_расч> t_табл, считают, что коэффициент значимости отличается от нуля, а между случайными величинами существует линейная статистическая связь.

4.2.2 Указания к выполнению работы. Пример

проведения корреляционного анализа

Тенденция изменения y от конкретного изменения x_J обнаруживается при достаточно большом числе N_J различных значений изменяемого фактора. Поэтому при планировании экспериментов для проведения корреляционного анализа необходимо предусматривать:

- большой диапазон изменения значений x_J;

- достаточное число N_J уровней факторов x_J при этом разница между уровнями должна быть больше абсолютной погрешности их измерения;

- проведение дублированных опытов (n) на каждом уровне фактора x_J;

- возможно большое общее число измерений (Nn).

1. Составление выборки пар чисел (x_J, y_J). Выборка составляется по графику одной из кривых на рисунке выбранного задания. Используем для нее зависимость К=j (а, j_в), где Кºy, aºx, j_в=40 град., на рис 5.1 лабораторной работы № 5.1. Снимаем выборку объемом N=9. Значения x и у по рис.5.1 запишем в табл. 4.1 (графы 2 и 3).

Таблица 4.1

Дата добавления: 2014-12-08