Постоянного тока

РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ

З А Д А Н И Е № 1

Дана электрическая схема с шестью ветвями, в каждой из которых есть либо источник ЭДС и сопротивление, или источник тока и сопротивление (источники ЭДС включены последовательно с сопротивлениями, источники тока – параллельно сопротивлениям). Положительным значениям ЭДС и источников токов в табл.1.1 соответствуют направления стрелок в ветвях (рис.1.1), отрицательным значениям – противоположные направления. Для нечетных вариантов предназначена схема – рис.1.1, а, для четных – рис.1.1, б.

Рис.1.1

Требуется:

1. Начертить схему для своего варианта задания, обозначить элементы, а значения их выписать рядом со схемой электрической цепи.

2. Рассчитать токи во всех ветвях методом контурных токов. Результаты свести в табл.1.2.

3. Написать систему уравнений по законам Кирхгофа, подставить в уравнения параметры цепи и найденные значения токов. Проверить правильность расчетов.

4. Подсчитать энергетический баланс в цепи.

Таблица 1.1

J6 A

–8

–5,2

7,5

–22

Е В

-59

R Ом

J5 A

–3,3

-14

2,2

–16

Е В

-28

–80

–23

R Ом

J4 A

5,5

–6

–2,2

–8

4,1

Е В

–26

–85

–26

R Ом

J3 A

1,4

–12

–4,3

3,8

Е В

–63

–23

–87

R Ом

J2 A

–4,7

–4

1,8

–1,1

Е В

–88

–23

R Ом

J1 A

–2,1

–10

1,5

–12

Е В

-63

-19

R Ом

№ ветви

МЭГ

вар.

продолжение таблицы 1.1

J6 A

–6,7

–7

Е В

–58

–74

–86

–53

R Ом

J5 A

–4,3

–31

Е В

-40

R Ом

J4 A

–15

–5

Е В

–32

–72

–44

R Ом

J3 A

–5

–1,8

–2,5

–11

Е В

–38

R Ом

J2 A

1,6

5,5

–3

Е В

–24

–30

–47

R Ом

J1 A

–4

–6,2

7,5

Е В

–36

–41

R Ом

№ ветви

МЭГ

вар.

продолжение таблицы 1.1

J6 A

–2,2

–26

–16

17,5

Е В

–70

–65

–2,8

R Ом

J5 A

–17

–9

–11,5

Е В

–49

–5,5

–15

–28,6

R Ом

J4 A

–16

–12

15,5

Е В

29,5

R Ом

J3 A

5,5

-9,5

Е В

–57

–32

3,5

–23

–15,4

R Ом

J2 A

6,5

–14

–7,5

–20

4,5

13,5

Е В

–82

–17,5

R Ом

J1 A

–3,5

–5

–7,5

Е В

–50

–1,5

–75

10,2

R Ом

№ ветви

МЭГ

вар.

Таблица 1.2

I11 A	I22 A	I33 A	I1 A	I2 A	I3 A	I4 A	I5 A	I6 A

5. Рассчитать токи во всех ветвях методом узловых потенциалов. Результаты свести в табл.1.3.

Таблица 1.3

j1 В	j2 В	j3 В	I1 A	I2 A	I3 A	I4 A	I5 A	I6 A

6. Построить потенциальную диаграмму для внешнего контура электрической цепи. Данные занести в табл.1.4.

Таблица 1.4

Точки контура		а	в	с	d	f	…
j, B
R, Ом

7. Методом эквивалентного генератора рассчитать и по-

строить график зависимости тока в указанной ветви (второй столбец в табл.1.1) от ее сопротивления. Расчетные данные свести в табл.1.5.

Таблица 1.5

R Ом	0	0,1×R	0,2×R	0,3×R	0,4×R	0,5×R	0,6×R	0,7×R	0,8×R	0,9×R	R
I А

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

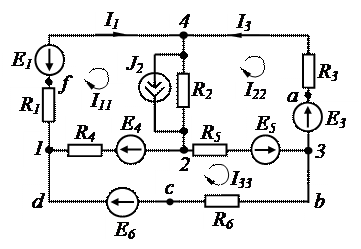1. Один из вариантов схемы электрической цепи показан на рис.1.2.

Рис.1.2

Вариант №…

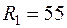Ом; В

Ом; В

Ом; В

Ом; В

Ом; В

Ом; А

Знак (–) указывает на противоположное направление источников по сравнению с рис.1.1,а.

2. Расчет цепи по методу контурных токов (МКТ).

2.1. Прежде, чем составлять уравнения по МКТ, необходимо все источники тока преобразовать в источники ЭДС. Например, источник тока преобразуется в источник ЭДС , а направление его определяется направлением источника тока (рис.1.3).

Рис.1.3

2.2. Определяем количество уравнений, которое необходимо и достаточно по МКТ. Оно равно числу независимых контуров :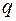

,

где 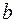– число ветвей в схеме, 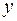– количество узлов.

2.3. Выбираем направление контурных токов (либо по часовой стрелке, либо против) и составляем систему уравнений в общем виде:

(1.1)

В выражении (1.1) , , 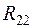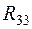– собственные сопротивления контуров (соответственно первого, второго и третьего), представляют собой суммы входящих в данный контур сопротивлений с положительными знаками:

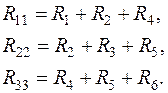
Сопротивления , , 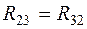называются взаимными сопротивлениями, которые являются сопротивлениями ветвей, общих для соответствующих контуров. Эти сопротивления берутся с отрицательными знаками:

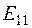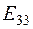, , – контурные ЭДС, представляющие собой алгебраические суммы ЭДС, входящих в контуры. Каждая ЭДС, входящая в эту сумму, берется с положительным знаком, если ее направление совпадает с контурным током, и, наоборот, - с отрицательным, если ее направление навстречу контурному току, например:

2.4. Система (1.1) решается относительно контурных токов 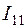, , . Для вычисления токов в ветвях зададимся направлением их, например, как показано на рис.1.1, а, тогда

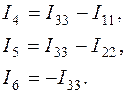
Отрицательные знаки токов в ветвях указывают на то, что их действительные направления противоположны первоначально выбранным. После вычисления токов в ветвях на схеме указать их истинные направления.

3. Прежде, чем составлять систему уравнений по законам Кирхгофа, определяется общее количество уравнений (необходимых и достаточных), которое должно равняться числу неизвестных токов, т.е. количеству ветвей 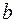. Количество уравнений, которое должно быть составлено по первому закону Кирхгофа, равно , где 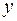– число узлов в схеме. Количество уравнений по второму закону Кирхгофа равно числу независимых контуров .

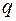3.1. Для любого узла (по первому закону Кирхгофа):

. (1.2)

Токи алгебраически суммируются, направленные к данному узлу берутся положительными, а от узла – отрицательными. Поскольку уравнения составляются для проверки правильности расчетов п.2, то следует учитывать истинные направления токов в ветвях.

3.2. Составляются уравнения по второму закону Кирхгофа:

. (1.3)

Напряжения в левой части (1.3) берутся положительными, если ток в ветви совпадает с направлением обхода контура, и – отрицательным, если не совпадает. ЭДС в правой части (1.3) берутся положительными, если они совпадают с направлением обхода контура, и – отрицательными при противоположном направлении.

3.3. В системы уравнений (1.2), (1.3) подставляются числовые значения и проверяются тождества уравнений. Совпадение правой и левой частей с погрешностью до 5 % можно считать удовлетворительным.

4. Энергетический баланс мощностей, рассеиваемых в сопротивлениях ветвей, и мощностей, развиваемых источниками энергии, проверяется с помощью уравнения:

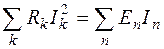. (1.4)

В левой части (1.4) – арифметическая сумма мощностей, выделяемых на сопротивлениях ветвей. В правой части – алгебраическая сумма произведений ЭДС источников на токи, протекающие через эти источники (с учетом истинного направления токов в ветвях). Если направления источника ЭДС и тока совпадают, то произведение берется с знаком плюс, если направления не совпадают, то – с знаком минус (это означает, что источник ЭДС данной ветви является потребителем электроэнергии).

5. Прежде, чем составлять систему уравнений по методу узловых потенциалов (МУП), определяется количество уравнений (необходимых и достаточных), которое равно .

5.1. Потенциал одного из узлов выбираем равным нулю, например, 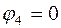, тогда согласно МУП:

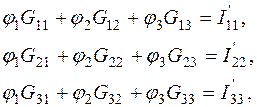(1.5)

где G₁₁, G₂₂, G₃₃ – суммы проводимостей всех ветвей, сходящихся в узлах соответственно 1, 2, 3; эти суммы всегда берутся с положительным знаком, например,

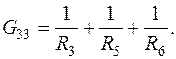
Проводимости , , 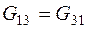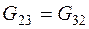определяются между соответствующими узлами 1 и 2, 1 и 3, 2 и 3; они берутся с отрицательными знаками, например,

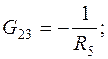
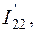
– узловые токи в узлах соответственно 1, 2, 3. Эти токи представляют собой алгебраическую сумму токов от источников ЭДС или источников токов. Если эти токи направлены к данному узлу, они берутся с плюсом, и, наоборот, - с минусом, если направлены от узла. Например, для схемы (рис.1.2)

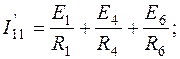
5.2. Система (1.5) решается относительно неизвестных потенциалов , , . После их определения токи в ветвях находятся с помощью закона Ома, например, для схемы (рис.1.2)

Если токи в ветвях получились отрицательными, это означает, что истинное их направление - противоположно.

6. Потенциальная диаграмма включает в себя расчет потенциалов на отдельных участках электрической цепи и графическое отображение изменения потенциала при обходе по контуру.

6.1. Токораспределение в схеме не изменится, если потенциал одного из узлов положить равным нулю, например, 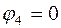(рис.1.2). Источник ЭДС повышает потенциал, если его направление совпадает с направлением обхода контура, и, наоборот, понижает, если - не совпадает. Падение напряжения на участке приводит к снижению потенциала, если направление тока совпадает с направлением обхода контура, и – к повышению потенциала при встречном направлении.

6.2. Строится система координат, по оси ординат которой откладываются значения потенциалов 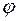, а по оси абсцисс – сопротивления 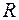(они суммируются по мере продвижения по контуру). Соответствующие точки со значениями потенциалов соединяют прямыми линиями. Обход внешнего контура совершить по часовой стрелке от потенциала .

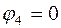7. Метод эквивалентного генератора (МЭГ) применяется для определения тока в какой-либо ветви сложной электрической цепи.

7.1. Для этого размыкается исследуемая ветвь и заданная схема вычерчивается с отключенной ветвью. Пассивная цепь, соответствующая схеме (рис.1.4, а), показана на рис.1.4, б.

7.2. Любым из методов, с подробными объяснениями, определяется напряжение на зажимах, от которых отключена ветвь (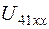). Это напряжение равно ЭДС эквивалентного генератора .

7.3. Определяем входное сопротивление 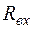со стороны клемм 4 –1 (рис.1.4, б) для пассивной цепи. Это сопротивление равно внутреннему сопротивлению эквивалентного генератора .

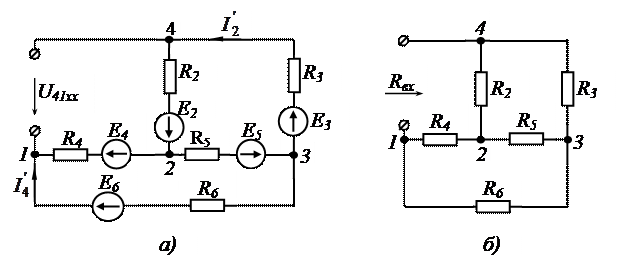
Рис.1.4

В некоторых случаях для нахождения 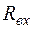удобно воспользоваться методом преобразования сопротивлений, соединенных звездой, в сопротивления, соединенные треугольником, как показано на рис.1.5. Между узлами 1, 2, 3 (рис.1.5, а) находится звезда из проводимостей (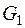, , 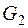), которая преобразуется в треугольник (, , ), показанный на рис.1.5, б, с помощью следующих соотношений:

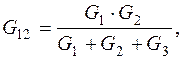
Рис.1.5

В других случаях, наоборот, удобно воспользоваться методом преобразования сопротивлений, соединенных треугольником (, , 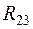между узлами 1, 2, 3, рис.1.6, а), в сопротивления, соединенные звездой (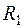, , 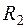, рис.1.6, б) с помощью выражений:

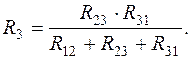
Рис.1.6

7.4. Согласно МЭГ по отношению к клеммам 4-1 можно начертить схему эквивалентного генератора (обозначенного пунктиром на рис.1.7) и первоначально удаленную ветвь 1, тогда

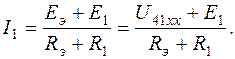(1.6)

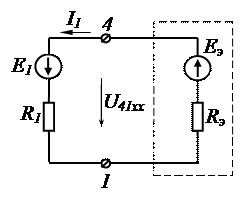Рис.1.7

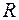7.5. Взять несколько значений сопротивления ветви (от до , где 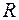– исходное значение сопротивления ветви, указанное в табл.1.1) и рассчитать точки по (1.6). Результат свести в табл.1.5.

Таблица 1.5

R Ом	0	0,1×R	0,2×R	0,3×R	0,4×R	0,5×R	0,6×R	0,7×R	0,8×R	0,9×R	R
I А

7.6. Построить зависимость тока в ветви от ее сопротивления. По оси абсцисс отложить 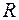, по оси ординат – ток.

Дата добавления: 2014-12-08