
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Переменного тока 2 страница
3.3. Комплексы взаимных сопротивлений контуров:
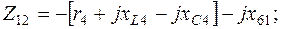
 (2.2)
(2.2)
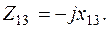
Слагаемые в квадратных скобках определяются по правилам, указанным в задании 1, а взаимно индуктивные составляющие – в зависимости от ориентации контурных токов относительно одноименных полюсов катушек (если контурные токи одинаково ориентированы относительно одноименных полюсов катушек, то 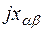 берется с знаком плюс, и, наоборот, при разной ориентации контурных токов это сопротивление учитывается с знаком минус).
берется с знаком плюс, и, наоборот, при разной ориентации контурных токов это сопротивление учитывается с знаком минус).
3.4. Комплексы собственных сопротивлений контуров:
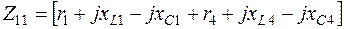 ;
;
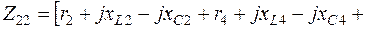
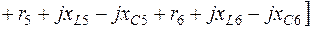 ; (2.3)
; (2.3)
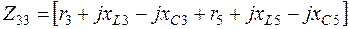 .
.
Взаимно индуктивные сопротивления учитываются в собственных сопротивлениях только тогда, когда есть индуктивные связи внутри данного контура (остальные правила – те же).
3.5. Комплексы контурных ЭДС:
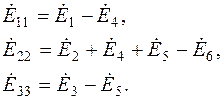 (2.4)
(2.4)
3.6. Система (2.1) решается относительно контурных токов 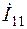 ,
, 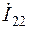 ,
, 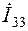 . Для вычисления токов в ветвях предварительно зададимся их направлениями, например, как показано на рис.2.1, тогда
. Для вычисления токов в ветвях предварительно зададимся их направлениями, например, как показано на рис.2.1, тогда
 (2.5)
(2.5)
Таблица 2.4
| Ток | 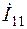 A
A
| 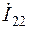 A
A
| 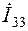 A
A
| 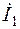 A
A
| 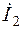 A
A
| 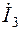 A
A
| 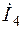 A
A
| 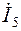 A
A
| 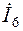 A
A
|
| Модуль | |||||||||
| Аргумент (град) |
3.7. Привести аналитические выражения для мгновенных значений токов ветвей ( ) и свести их в табл.2.5.
) и свести их в табл.2.5.
Таблица 2.5
| Ветвь | 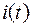 , A , A
| 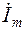 , A , A
| 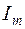 , A , A
| 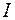 , A , A
|
4. Прежде, чем составлять систему уравнений по законам Кирхгофа, определяется общее количество необходимых уравнений. Оно равно числу ветвей в схеме – 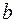 . Количество уравнений по первому закону Кирхгофа – (
. Количество уравнений по первому закону Кирхгофа – (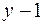 ), где
), где 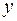 – число узлов. Число уравнений по второму закону Кирхгофа равно
– число узлов. Число уравнений по второму закону Кирхгофа равно 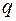 .
.
4.1. Система уравнений в символической форме по первому закону Кирхгофа имеет вид:
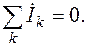 (2.6)
(2.6)
Раскроем подробнее выражение (2.6) для узлов 1, 2, 3 соответственно (рис.2.3, а направление токов в ветвях - см. рис.2.1):
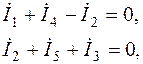 (2.7)
(2.7)
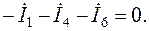
4.2. Система уравнений в символической форме по второму закону Кирхгофа:
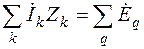 (2.8)
(2.8)
составляется так же, как и в цепях постоянного тока, но появляются слагаемые, связанные с взаимной индуктивностью, которые учитываются по следующему правилу. Если направление обхода элемента m и ток в ветви с элементом n одинаково ориентированы по отношению к одноименным полюсам индуктивности, то 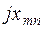 берется с положительным знаком, и, наоборот, если направление обхода элемента m и ток в ветви с элементом n по разному ориентированы по отношению к одноименным полюсам индуктивности, то
берется с положительным знаком, и, наоборот, если направление обхода элемента m и ток в ветви с элементом n по разному ориентированы по отношению к одноименным полюсам индуктивности, то 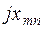 имеет знак минус. Поэтому выражения (2.8) для первого, второго и третьего контуров (рис.2.3) соответственно примут вид (направления обхода контуров – по часовой стрелке):
имеет знак минус. Поэтому выражения (2.8) для первого, второго и третьего контуров (рис.2.3) соответственно примут вид (направления обхода контуров – по часовой стрелке):
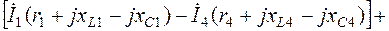
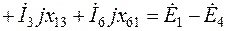 , (2.9)
, (2.9)
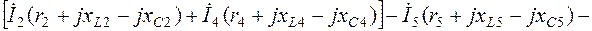
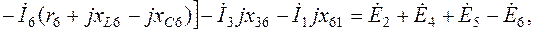 (2.10)
(2.10)
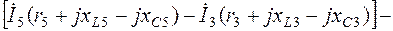
 (2.11)
(2.11)
Погрешность выполнения равенств (2.9) ¸ (2.11) находится отдельно для вещественных и мнимых частей, в каждом случае она не должна превышать пяти процентов.
Выписать и свести в таблицу значения ЭДС в каждой ветви.
Таблица 2.6
| Ветвь | 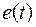 , B , B
| 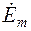 , B , B
| 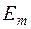 , B , B
| 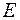 , B , B
|
5. Прежде, чем строить векторную диаграмму по, например, первому контуру, необходимо составить уравнение по второму закону Кирхгофа (уравнение (2.9)) и вычислить все составляющие этого уравнения.
На комплексной плоскости выбирается масштаб для векторов напряжения и строится векторная диаграмма на миллиметровой бумаге. При правильном построении векторы, просуммированные по правилу многоугольника, например, в левой части выражения (2.9), совпадут с геометрической суммой векторов (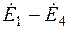 ) в правой части.
) в правой части.
6. Энергетический баланс мощностей, развиваемых источниками ЭДС и потребляемых в цепи, проверяется следующим образом.
6.1. Для активных мощностей:
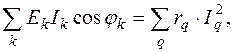 (2.12)
(2.12)
где в левой части – алгебраические суммы активных мощностей источников,  . Если мощность окажется отрицательной (
. Если мощность окажется отрицательной (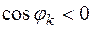 ), то это означает, что данный источник потребляет активную мощность (например, вместо генератора - электродвигатель). В правой части (2.12) – арифметическая сумма мощностей, рассеиваемых на активных сопротивлениях. Подробная запись (2.12) для схемы (рис.2.3) имеет вид:
), то это означает, что данный источник потребляет активную мощность (например, вместо генератора - электродвигатель). В правой части (2.12) – арифметическая сумма мощностей, рассеиваемых на активных сопротивлениях. Подробная запись (2.12) для схемы (рис.2.3) имеет вид:
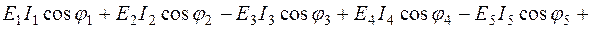
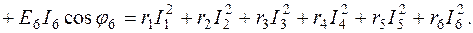 (2.13)
(2.13)
Если направление источника ЭДС и тока ветви не совпадает, то слагаемые в левой части берутся с знаком минус.
6.2. Для реактивных мощностей:
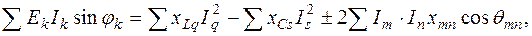 (2.14)
(2.14)
где в левой части – алгебраическая сумма реактивных мощностей источников. Если мощность отрицательная (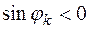 ), значит источник потребляет реактивную мощность. В правой части (2.14) первое слагаемое – реактивные индуктивные мощности, второе слагаемое – реактивные емкостные мощности, третье слагаемое – реактивные мощности, обусловленные взаимно индуктивными связями между катушками (
), значит источник потребляет реактивную мощность. В правой части (2.14) первое слагаемое – реактивные индуктивные мощности, второе слагаемое – реактивные емкостные мощности, третье слагаемое – реактивные мощности, обусловленные взаимно индуктивными связями между катушками (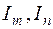 – действующие значения токов в ветвях взаимно связанных катушек,
– действующие значения токов в ветвях взаимно связанных катушек, 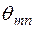 – угол сдвига между начальными фазами токов в ветвях,
– угол сдвига между начальными фазами токов в ветвях, 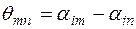 ). Знак плюс берется при согласном включении катушек, а минус – при встречном включении. Подробная запись выражения (2.14):
). Знак плюс берется при согласном включении катушек, а минус – при встречном включении. Подробная запись выражения (2.14):
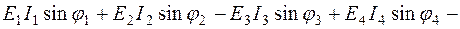
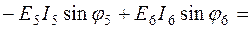
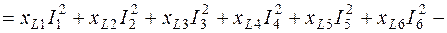 (2.15)
(2.15)
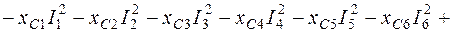

где 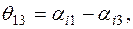
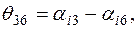
 Значения
Значения 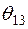 ,
, 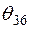 ,
, 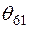 нетрудно определить из табл.2.4.
нетрудно определить из табл.2.4.
Согласное или встречное включение катушек в правой части выражения (2.14) определяется ориентацией токов в ветвях по отношению к одноименным полюсам катушек (если токи в индуктивно связанных ветвях одинаково ориентированы по отношению к одноименным полюсам, то включение – согласное, и, наоборот, если токи в ветвях по разному ориентированы по отношению к одноименным полюсам катушек, то включение – встречное).
П Р И М Е Р
1. Пусть задано: 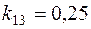 ;
; 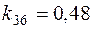 ;
; 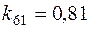 ;
; 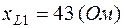 ;
; 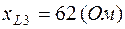 ;
; 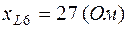 , тогда
, тогда
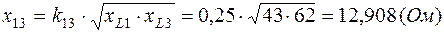 ,
,
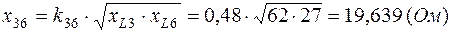 ,
,
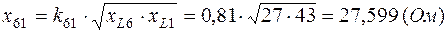 .
.
2. Один из вариантов схемы приведен на рис.2.2, где
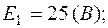
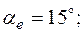
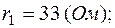
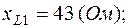
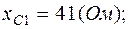
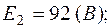
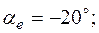
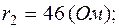
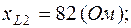
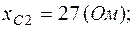

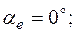
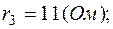
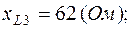
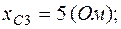

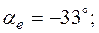
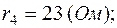
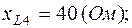
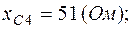

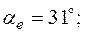
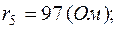
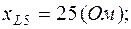
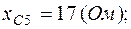
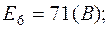
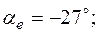
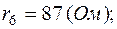
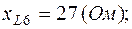
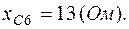
Схема в символической форме показана на рис.2.3, где

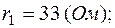

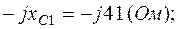
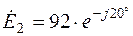 (В);
(В); 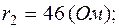
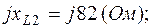
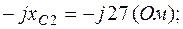
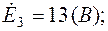
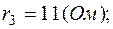
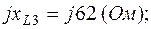
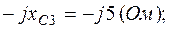
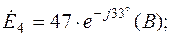
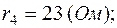
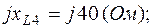

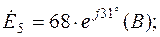
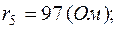
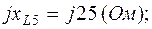
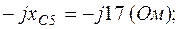
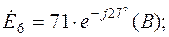
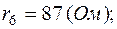
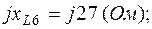
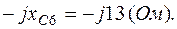
3. Расчет цепи методом контурных токов.
3.1. Определяем количество уравнений: 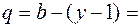 = 6 – (4 – 1) = 3, где
= 6 – (4 – 1) = 3, где 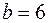 ,
, 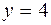 .
.
3.2. Выбираем направление контурных токов (по часовой стрелке, рис.2.2, 2.3) и составляем систему уравнений:
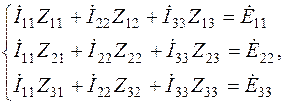 (2.1)
(2.1)
3.3. Рассчитаем комплексы взаимных сопротивлений между контурами согласно (2.2):

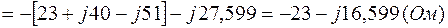 ;
;
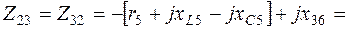
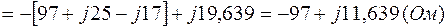 ;
;
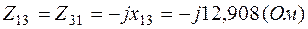 .
.
3.4. Определяем по (2.3) комплексы собственных сопротивлений контуров:
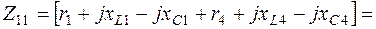
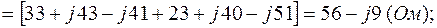
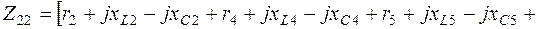
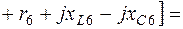
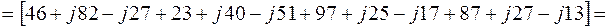
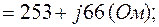
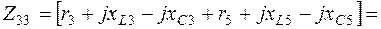

3.5. Комплексы контурных ЭДС согласно (2.4) равны:
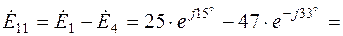
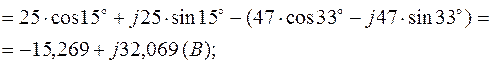

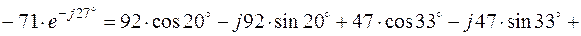
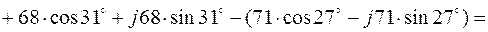
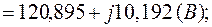
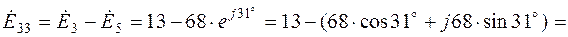
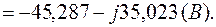
3.6. Решение системы (2.1) дает:
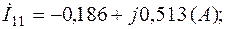
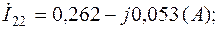
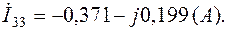
Токи в ветвях с учетом (2.5):
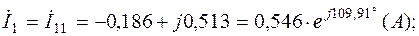
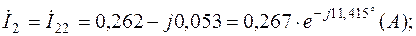
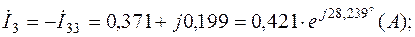
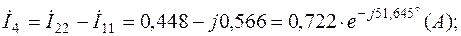
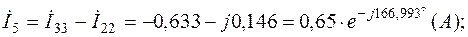
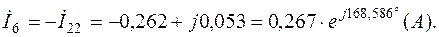
Значения контурных токов и токов в ветвях сведены в табл.2.4.
Таблица 2.4
| Ток | 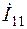 A
A
| 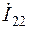 A
A
| 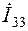 A
A
| 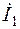 A
A
| 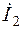 A
A
| 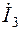 A
A
| 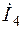 A
A
| 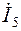 A
A
| 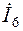 A
A
|
| Модуль (А) | 0,546 | 0,267 | 0,421 | 0,546 | 0,267 | 0,421 | 0,722 | 0,65 | 0,267 |
| Аргумент (град) | 109,91 | -11,415 | 208,239 | 109,91 | -11,415 | 28,239 | -51,645 | -166,993 | 168,586 |
3.7. Аналитические выражения для мгновенных значений токов в ветвях нетрудно получить из табл.2.4. Например, для первой ветви 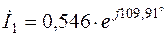 , поэтому
, поэтому 
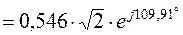 , где
, где 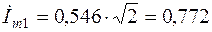 , а мгновенное значение тока
, а мгновенное значение тока 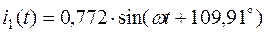 . Остальные токи приведены в табл.2.5.
. Остальные токи приведены в табл.2.5.
Таблица 2.5
| Ветвь | 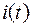 , А , А
| 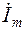 , A , A
| 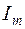 , A , A
| 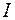 , A , A
|
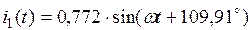
| 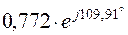
| 0,772 | 0,546 | |

| 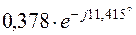
| 0,378 | 0,267 | |
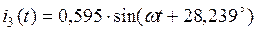
| 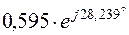
| 0,595 | 0,421 | |
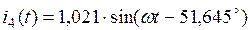
| 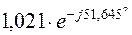
| 1,021 | 0,722 | |
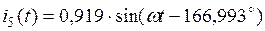
| 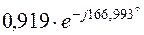
| 0,919 | 0,65 | |
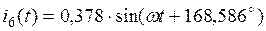
| 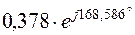
| 0,378 | 0,267 |
4. Общее количество уравнений по законам Кирхгофа: 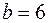 . Число уравнений по первому закону Кирхгофа:
. Число уравнений по первому закону Кирхгофа: 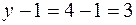 . Количество уравнений по второму закону Кирхгофа:
. Количество уравнений по второму закону Кирхгофа: 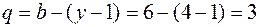 .
.
4.1. Проверим справедливость системы (2.7):
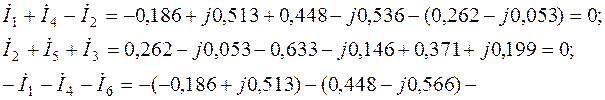
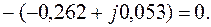
4.2. Оценим тождественность уравнения (2.9):

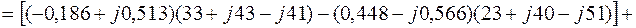
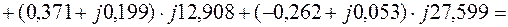
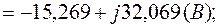
С другой стороны:
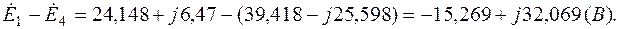
Уравнение (2.10):
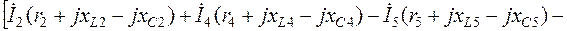
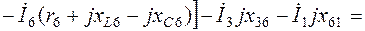
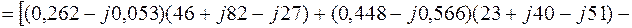
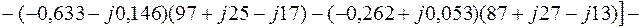
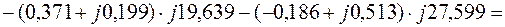
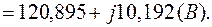
С другой стороны:
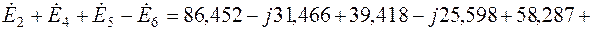
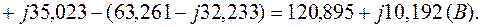
Уравнение (2.11):
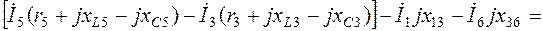
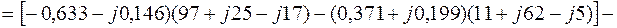
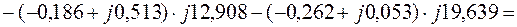
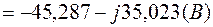 .
.
С другой стороны:
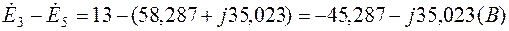 .
.
В каждом уравнении погрешность в пределах нормы.
Мгновенные значения ЭДС для всех ветвей сведены в табл.2.6.
Таблица 2.6
| Ветвь | 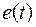 , В , В
| 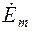 , В , В
| 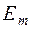 , В , В
| 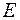 , В , В
|
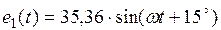
| 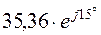
| 35,36 | ||

| 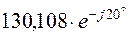
| 130,108 | ||
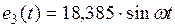
| 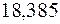
| 18,385 | ||
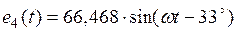
| 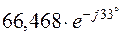
| 66,468 | ||
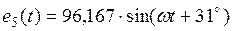
| 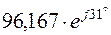
| 96,167 | ||
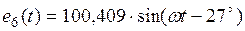
| 
| 100,409 |
|
|
Дата добавления: 2014-12-08; Просмотров: 365; Нарушение авторских прав?; Мы поможем в написании вашей работы!