П р и м е р

1. Вариант схемы и значения элементов приведены на рис.1.2.

2. Расчет цепи по методу контурных токов (МКТ).

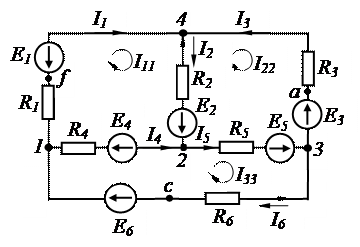2.1. Схема (рис.1.2) с преобразованным источником тока имеет вид, показанный на рис.1.8, где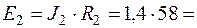 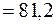(В).

Рис.1.8

2.2. Определяем количество уравнений по МКТ:

, где , .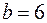

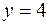2.3. Составляем систему уравнений:

(1.1)

где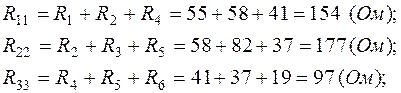

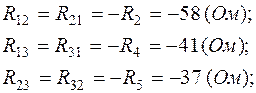
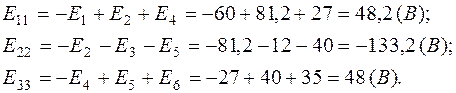
Система (1.1) примет вид:

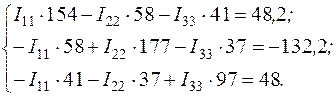
2.4. Решение системы дает: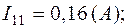

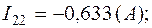
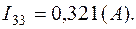
Токи в ветвях:

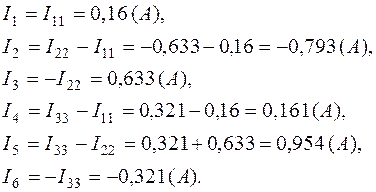
Истинные направления токов 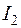и 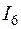указаны дополнительными стрелками на рис.1.8, а их значения сведены в табл.1.2.

Таблица 1.2

I11 А	I22 А	I33 А	I1 А	I2 А	I3 А	I4 А	I5 А	I6 А
0,16	-0,633	0,321	0,16	0,793	0,633	0,161	0,954	0,321

3. Количество уравнений по первому закону Кирхгофа равно 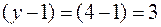. Число уравнений по второму закону Кирхгофа: . Общее количество уравнений .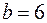

3.1. Система уравнений по первому закону Кирхгофа для 1, 2, 3 узлов схемы (рис.1.8):

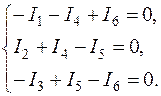
3.2. Система уравнений по второму закону Кирхгофа для схемы (рис.1.8):

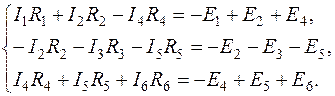
3.3. Подставляем числовые значения и проверяем тождество уравнений:

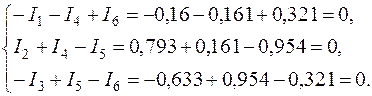
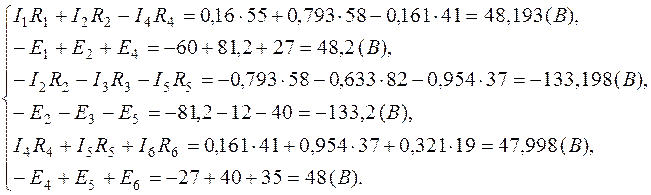
4. Энергетический баланс мощностей:

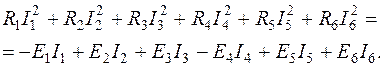
Подставим числа:

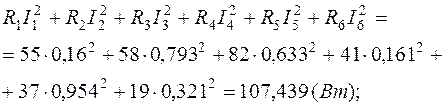
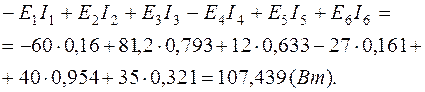
5. Расчет цепи по МУП. Количество уравнений согласно данному методу равно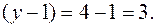

5.1. Система уравнений по методу узловых потенциалов (полагаем ):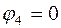

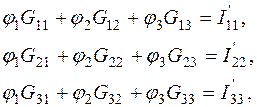(1.5)

где

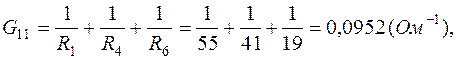
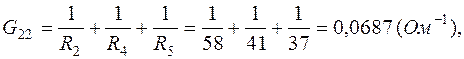
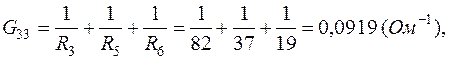
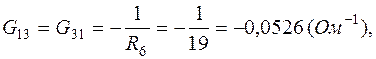
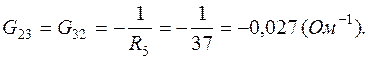
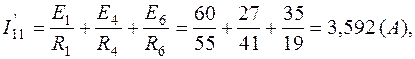
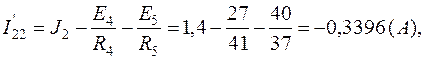
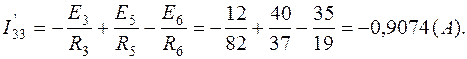
После подстановки численных данных в (1.5):

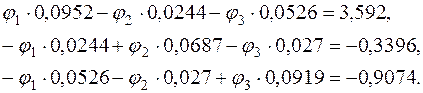
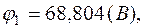
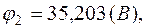
5.2. Система решается относительно узловых потенциалов: 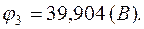Зная потенциалы в узлах, определим токи в ветвях:

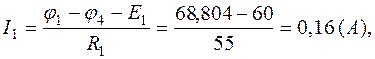
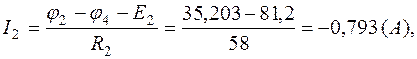
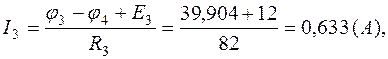
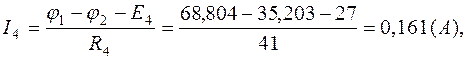
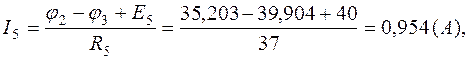
Расчетные значения потенциалов и токов сведены в табл.1.3.

Таблица 1.3

j1 В	j2 В	j3 В	I1 А	I2 А	I3 А	I4 А	I5 А	I6 А
68,804	35,203	39,904	0,16	0,793	0,633	0,161	0,954	0,321

6. Потенциальная диаграмма.

6.1. Обойдем внешний контур (рис.1.8) по часовой стрелке, положив ():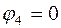

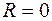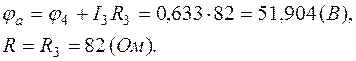
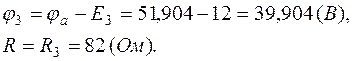
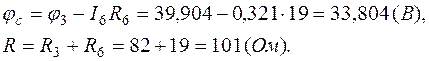
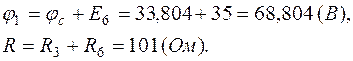
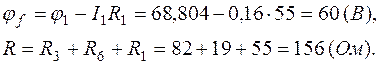
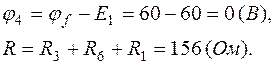
Таким образом, мы возвратились в точку 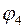, но координата 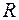равна сумме всех сопротивлений вдоль пройденного контура.

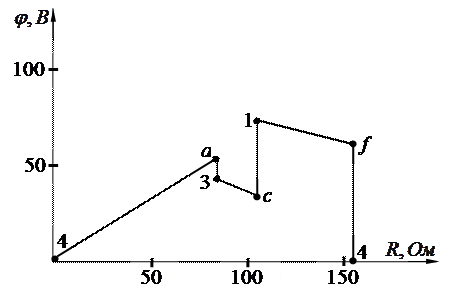6.2. Потенциальная диаграмма построена на рис.1.9, а координаты каждой точки () сведены в табл.1.4.

Рис.1.9

Таблица 1.4

Точки контура		а		с		f
j, В		51,904	39,904	33,804	68,804
R, Ом

7. Методом эквивалентного генератора рассчитать ток, например, в 1 ветви.

7.1. Схемы цепи для определения напряжения холостого хода и 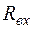приведены на рис.1.4.

7.2. Методом двух узлов найдем напряжение между узлами 3–2:

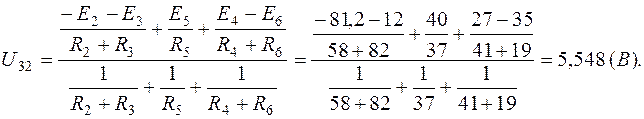
Токи 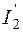(через сопротивление 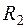), 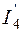(через сопротивление R₄, рис.1.4, а) определим по закону Ома для участка цепи, содержащего ЭДС:

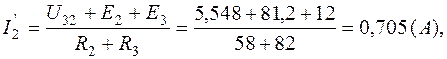
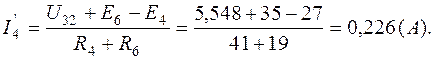
Обойдем воображаемый контур (рис.1.4, а), по второму закону Кирхгофа: 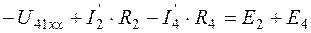, поэтому

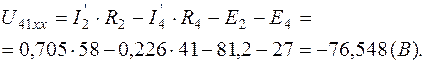
Знак минус указывает на то, что направление 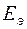от узла 4 к узлу 1.

7.3. Заменим треугольник сопротивлений (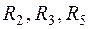) между узлами 4, 3, 2 (рис.1.4, б) на звезду сопротивлений (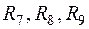, рис.1.10):

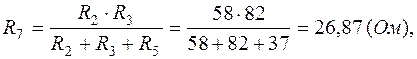
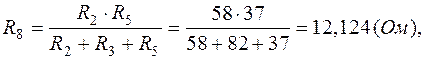
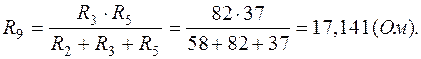
Исходная схема (рис.1.4, б) примет вид, показанный на рис.1.10, где

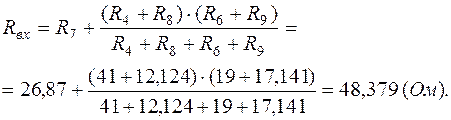
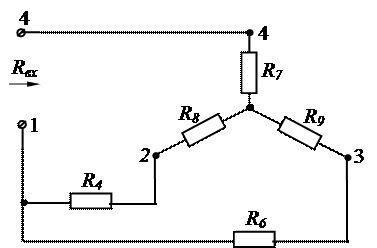Рис.1.10

7.4. Эквивалентный генератор показан на рис.1.7, где 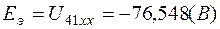(знак минус указывает на противоположное направление 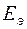), , 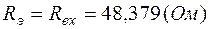поэтому ток в первой ветви:

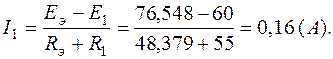
7.5. При различных сопротивлениях ветви (от 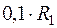до 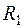) рассчитаем ток в ветви 1 по МЭГ. Эти числа сведены в табл.1.5.

Таблица 1.5

R1 Ом		5,5		16,5		27,5		38,5		49,5
I1 А	0,342	0,307	0,279	0,255	0,235	0,218	0,203	0,19	0,179	0,169	0,16

7.6. График зависимости тока в ветви 1 от ее сопротивления дан на рис.1.11.

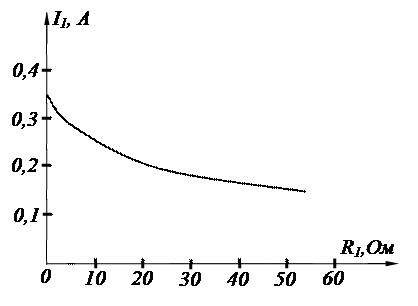Рис.1.11

Дата добавления: 2014-12-08