
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поглощение света. Поглощение света определяется законом бугера-ламберта: (1) или
|
|
|
|
Задача № 135 ( 5 баллов ) Решение: (РОФ, 2010)
 Поглощение света определяется законом Бугера-Ламберта:
Поглощение света определяется законом Бугера-Ламберта: 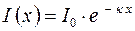 (1) или
(1) или  (2),
(2),
где n - число, определяющее, во сколько раз уменьшилась интенсивность света.
1-й способ:
Несложно показать, что  n величина аддитивная, то есть для многослойного вещества со слоями разной толщины x и с разными коэффициентами поглощения k выполняется равенство для итогового значения
n величина аддитивная, то есть для многослойного вещества со слоями разной толщины x и с разными коэффициентами поглощения k выполняется равенство для итогового значения  n:
n:
 (3).
(3).
Обозначим толщину старых и новых штор, а также занавески из тюля соответственно через x1 x2 и x3. Пусть коэффициент поглощения льна равен λ, а коэффициент поглощения тюля – τ. Тогда условия задачи запишутся в следующем виде:
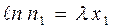 (только для старых льняных штор) (4),
(только для старых льняных штор) (4), 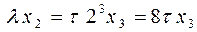 (так как
(так как 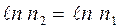 ) (5),
) (5),
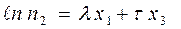 (6).
(6).
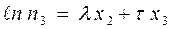 (7).
(7).
Учитывая, что по условию  , определим искомое число:
, определим искомое число: 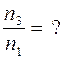
Кроме того, запишем: x2 = 3 x1 (6)
(так как площадь поверхности и плотность льняных штор не меняется, а они при этом содержат воды в три раза больше (сохнут в три раза дольше), то они соответственно толще старых штор в три раза).
Вычитая из (7) выражение (4), получим:
 или
или
 или
или  или
или 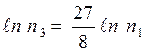 (8).
(8).
С другой стороны, вычитая из (6) уравнение (4), найдём:
 (9). Отсюда найдём:
(9). Отсюда найдём:  (10).
(10).
Из (10) найдём:  (11).
(11).
Из (8) и (11) получим, вычитая данные уравнения:

 или
или 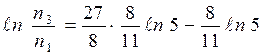 или
или 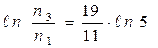 (12).
(12).
Отсюда окончательно получим искомое число:
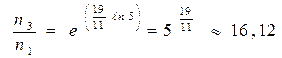 . Отметим, что, вначале, по-сравнению с улицей, освещённость в квартире уменьшалась в
. Отметим, что, вначале, по-сравнению с улицей, освещённость в квартире уменьшалась в 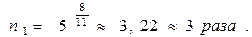 ,а новые шторы и тюль дают, по-сравнению с улицей, снижение освещённости в комнате в
,а новые шторы и тюль дают, по-сравнению с улицей, снижение освещённости в комнате в  раза.
раза.
Таким образом, определили:

2-й способ:
Так как из закона Бугера –Ламберта 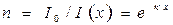 (2),
(2),
где n - число, определяющее, во сколько раз уменьшилась интенсивность света, то:
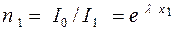 (для одних старых штор) (3).
(для одних старых штор) (3).
 (для тюля и старых штор) (4).
(для тюля и старых штор) (4).
 (для новых штор и тюля) (5).
(для новых штор и тюля) (5).
По условию:
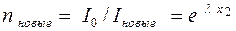 =
= 
(новые шторы, по-сравнению с тюлем) или 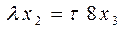 (6).
(6).
Кроме того, запишем: x2 = 3 x1 (7).
С учётом (6) и (7) перепишем (2) - (5):
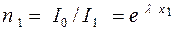 (для одних старых штор) (3).
(для одних старых штор) (3).
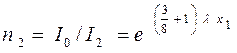 (для тюля и старых штор) (4).
(для тюля и старых штор) (4).
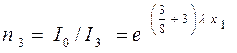 (для новых штор и тюля) (5).
(для новых штор и тюля) (5).
Отсюда найдём  , зная, что по условию
, зная, что по условию  :
:
 (6).
(6).
Тогда окончательно найдём:
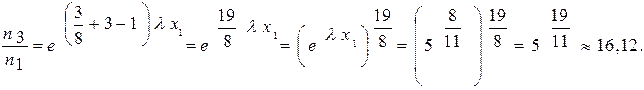
3-й способ:
Рассмотрим величину k j, показывающую - во сколько раз уменьшается интенсивность излучения после прохождения z слоёв некоторого вещества. Другими словами, будем рассматривать величину обратную коэффициенту пропускания данного вещества.
Можно показать, что результирующее значение k j рез равно произведению k j для соответствующего количества слоёв вещества z:
 (1).
(1).
Обозначим соответствующие коэффициенты тюля и льна через  и
и  . Здесь
. Здесь  и
и 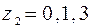 (рассматриваемое количество слоёв какого-либо материала: например, при начальной освещённости на улице
(рассматриваемое количество слоёв какого-либо материала: например, при начальной освещённости на улице  и
и  (то есть, в его отсутствие); для одного слоя тюля
(то есть, в его отсутствие); для одного слоя тюля  , а для тюля, сложенного трижды пополам
, а для тюля, сложенного трижды пополам  ; для старых штор из льна
; для старых штор из льна 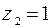 и, поскольку новые шторы в три раза толще, то для них
и, поскольку новые шторы в три раза толще, то для них  ).
).
Тогда с учётом условий задачи и, выбирая требуемые значения z, запишем систему уравнений:

Решая данную систему уравнений несложно определить искомое значение x, а также m,  и
и  .
.
Получим:
 (6),
(6),  (7). Кроме того, определим значения
(7). Кроме того, определим значения  и
и  :
:
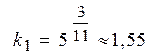 (8),
(8), 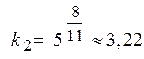 (9).
(9).
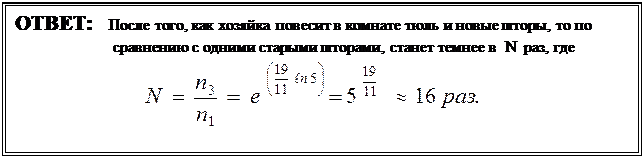
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 551; Нарушение авторских прав?; Мы поможем в написании вашей работы!