Прикладная механика 1 страница

Буторин Л.В., Балакин Ю.А., Шевелев И.А, Бусыгина Е.Б.

ПРИКЛАДНАЯ МЕХАНИКА

Юрий Александрович Балакин

Дополнительная

Основная

1. Сурин В.М. Прикладная механика. Новое знание, 2008, 392с

2. Бегун. П.И., Кормилицын О.П. Прикладная механика. Политехника, 2006, 464с.

3. Марченко С.И., Марченко Е.П. Прикладная механика. Феникс, 2006, 544с.

4. Прикладная механика: Учебник для ВУЗов под ред. Джамая В.В. Дрофа, 2004, 416с.

1. Фролов К.В., Попов С.А., Мусатов А.К. и др. Теория механизмов и механика машин, М: МГТУ им. Н.Э.Баумана, 2005,

2. Феодосьев В.И. Сопротивление материалов. М: МГТУ им. Н.Э.Баумана, 2005, 590 с. (все годы издания).

3. Дунаев П.Ф., Леликов О.П. Конструирование узлов и деталей машин. Акадкмия, 2008, 496с.

4.Детали машин под.ред. Ряховского О.А. - М.:МГТУ им.Н.Э. Баумана, 2007,515с.

5. Чернилевский Д.В. Детали машин. Проектирование приводов технологического оборудования. Машиностроение, 2003, 408с.

6. Балдин В.А. Галевко В.В. Детали машин и основыконструирования. Передачи. Академкнига, 2006, 336с.

7. Махова Н.С., Поболь О.Н., Семин М.И. Основы теории механизмов и машин. Владос, 2006, 288с.

8. Иванов М.Н., Финогенов В.А. Детали машин. Высшая школа, 2008, 408с.

Иван Андреевич Шевелев

Леонид Васильевич Буторин

Самостоятельная работа по дисцеплине

Подписано к печати:

Учебно-практическое пособие для студентов

специальностей 220301 заочной формы обучения

Москва 2011

УДК 531.8

© Буторин Л.В., Балакин Ю.А., Шевелев И.А., Буыгина Е.Б. Прикладная механика. Учебно-практическое пособие. - М., МГУТУ, 2011.

В учебно-практическом пособии в кратком и систематическом виде изложено содержание курса прикладная механика. Пособие состоит из трех разделов: теория механизмов и машин, сопротивление материалов, детали машин. После каждой темы даны вопросы и тесты, позволяющие контролировать степень усвоения материала. Имеются словари основных понятий и терминов.

Пособие предназначено для студентов заочной формы обучения по специальностям 220301.

Авторы: Буторин Леонид Васильевич, Балакин Юрий Александрович, Шевелев Иван Андреевич, Бусыгина Елена Борисовна.

Рецензенты: Бардовский А.Д. профессор кафедры теоретической и прикладной механики МГГУ, д.т.н.

Щеглов С.В. доцент кафедры инженерной графики и проектирования МГВМИ.

Редактор Свешникова Н.И.

© Московский государственный университет технологий управления

109004; Москва, Земляной вал 73, 2011 г.

Содержание

Введение………………………………………………………………………..4

Раздел 1. Теория машин и механизмов……………………………………..…...4

1.1.Основные понятия и пределения………………………………………….....4

1.2.Классификация кинематических пар, кинематических цепей

и механизмов……………………………………………………………………....5

1.3.Структурный анализ и синтез механизмов…………………………….........6

1.4.Кинематический анализ механизмов с низшими парами…………………..7

1.5.Силовой анализ механизмов………………………………………………….9

1.6.Уравнения движения механизмов…………………………………………...11

1.7.Решение уравнений движения механизмов…………………………………14

Тесты к разделу «Теория машин и механизмов».…………………………15

Вопросы к разделу «Теория машин и механизмов» ……………………….17

Раздел 2. Сопротивление материалов ………………………………...18

2.1.Основные понятия и определения…………………………………………...18

2.2.Метод сечений. Виды деформаций………………………………………….22

2.3.Механические характеристики материалов……………………………..….25

2.5.Принцип расчета на прочность, жесткость………………………………....28

Тесты к разделу "Сопротивление материалов"…..………………………....31

Вопросы к разделу "Сопротивление материалов".. ………………….31

Раздел 3. Детали машин……………………………………………………….….32

3.1.Основные понятия………………………………………………………….…32

3.2.Соединение деталей…………………………………………………………..33

3.3.Механические передачи……………………………………………………....38

3.4.Валы, оси и опоры………………………………………………………….…46

Тесты к разделу «Детали машин»………………………………………….…49

Вопросы к разделу «Детали машин»…………………………………………50

4.Решение тренировочных заданий……………………………………………...51

Ответы на тесты к разделам…………………………………………………..59

Тесты по дисциплине "Прикладная механика"……..…………………….....60

Ответы на тесты по дисциплине «Прикладная механика»……………….…61

Словарь основных понятий и терминов …………………………………………61

Список рекомендуемой литературы……………………………………………..65

Приложение………………………………………………………………………..66

Введение

Прикладная механика - дисциплина, состоящая из трех основных разделов: теория механизмов и машин, сопротивление материалов, детали машин.

ТММ изучает общие методы исследования свойств механизмов и машин, а также способы проектирования их схем независимо от конкретного назначения машины, прибора или аппарата.

Сопротивление материалов изучает инженерные методы расчетов элементов конструкций на прочность, жесткость и устойчивость с целью обеспечения требуемой надежности и экономичности, минимальной материалоёмкости.

В разделе курса «Расчет деталей машин» рассматриваются теоретические основы расчета и конструирования типовых деталей и узлов машин.

Раздел 1. Теория механизмов и машин

1.1. Основные понятия и определения

Механизм - это система твердых тел, предназначенная для преобразования движения одного или нескольких тел в требуемые движения других тел.

Тела (абсолютно твердые и гибкие), входящие в состав механизма, называют его звеньями. Механизм имеет не менее двух звеньев. Соединение двух соприкасающихся звеньев, обеспечивающее их относительное движение называется кинематической парой (КП).

Как правило, одно из звеньев механизма неподвижно или считается неподвижным и называется стойкой, все другие звенья - подвижные. Среди звеньев есть два смежных звена, закон относительного движения которых известен. КП, которая соединяет эти звенья, называется входной. Звено, образующее входную КП со стойкой, называется входным. Оно сообщает движение другим звеньям механизма. Выходное звено - подвижное звено, совершающее движения, для выполнения которых предназначен механизм.

Кинематическая цепь (КЦ) - система звеньев, связанных между собой одной или более КП.

Структурная схема - схема механизма, указывающая стойку и подвижные звенья, входную КП или входное звено, а также виды КП. Структурная схема выполняется с учетом стандартных условных обозначений, применяемых при графическом изображении звеньев и КП. На рис. 1.1. а) и б) приведены структурные схемы распространенных рычажных механизмов называемых шарнирными: а) четырехзвенником; б) шестизвенником.

0 0

а) б)

Рис. 1.1

Обозначения следующие: 0 - стойка; 1,2,3, и т.д. - подвижные звенья; 1,А - входное звено и КП соответственно; j - координата, КП, обозначаемая латинскими буквами, иногда с указанием соединяемых звеньев.

1.2..Классификация КП, кинематических цепей и механизмов

КП состоит из элементов - совокупности поверхностей, линий и отдельных точек звеньев,по которым одно соприкасается с другим звеном, образуя КП, которые делятся на низшие и высшие.

Низшая КП получается относительным движением двух звеньев, соприкасающихся по поверхности, а высшая КП, в которой указанное движение звеньев получается соприкосновением ее элементов только по линиям или в точках.

Обозначим: W - число степеней свободы в относительном движение звеньев, образующих КП; S - число уравнений связей, налагаемых на относительное движение этих звеньев. Тогда всегда выполняется равенство:

W + S = 6.

Отсюда была предложена классификация КП: во-первых, по числу связей (одно-, двух-, трех-, четырех- и пяти-подвижные); во-вторых, по числу уравнений связей (S), которое принято за N - номер класса КП (пары пятого, четвертого, третьего, второго и первого класса).

В зависимости от относительного движения звеньев КП бывают различного вида. Различают девять видов КП. Они приведены в приложении.

Познакомимся с классификацией КЦ механизмов. Они подразделяются на: 1) плоские и пространственные; 2) замкнутые и незамкнутые.

Если при закреплении одного звена, точки всех других звеньев могут двигаться во взаимно параллельных плоскостях, то образуется плоская КЦ. При не выполнении этого условия - пространственная КЦ.

В незамкнутой КЦ есть хотя бы одно звено, входящее в одну КП. В замкнутой КЦ каждое звено входит в две КП, т.е. звенья такой цепи образуют одно или несколько замкнутых контуров (см. рис. 1.2 а) и б)).

а) б)

Рис. 1.2

Различают три классификации механизмов:

объемные и поверхностные по виду траектории точек звеньев;

c замкнутыми и незамкнутыми КЦ;

с низшими и высшими КП.

В технике наиболее распространены плоские четырехзвенные рычажные механизмы - шарнирный четырехзвенник (см. рис. 1.1 а)); кривошипно-ползунный и кулисный механизмы, а также механизмы с высшими парами - зубчатый, кулачковый и комбинированные.

Более подробно о разновидностях механизмов см. [1, c. 6-23]. Изучив основные понятия ТММ, можно переходить к исследованию структуры механизмов.

1.3.Структурный анализ и синтез механизмов

Звенья, соединяясь между собой КП, образуют структуру механизма, его структурную цепь, изображаемую графически структурной схемой. Строение этой цепи предопределяет основные технические характеристики механизма, такие, как число степеней свободы возможные законы движения звеньев, возможное преобразование движений, и др. Основные структурные характеристики: тип структурной цепи, число степеней свободы механизма, наличие и типы структурных групп. Различают типы структурных цепей: пространственные – плоские, замкнутые – разомкнутые, сложные – простые (определения см. [2, с. 30], и др.).

Под числом степеней свободы механизмов с голономными связями будем понимать число возможных независимых перемещений, которые могут быть сообщены звеньям механизма. Число степеней свободы механизмов определяют по структурным формулам [1, с. 26-31].

Для механизмов с пространственной структурной схемой

W = 6n – 5P₁ – 4P₂ – 3P₃ – 2P₄ – P₅

Для механизмов с плоской структурной схемой

W = 3n – 2P₁ – Р₂,

где n – число подвижных звеньев;

Р₁ – число кинематических пар с одной степенью свободы;

Р₂ – число кинематических пар с двумя степенями свободы и т.д.

Основные типы и характеристики КП приведены в приложении.

Синтез и анализ механизмов существенно упрощаются при использовании понятия структурной группы (группы Ассура).

Структурной группой называют кинематическую цепь, степень свободы которой равна нулю и которая не раскладывается на более простые группы с тем же свойством. Структурные группы обладают важнейшим свойством: они статически и кинематически определимы [2, с. 59]. Это свойство позволяет заменить исследование многозвенного механизма последовательным исследованием его структурных групп, что существенно упрощает решение задачи.

Поиск структурных групп следует начинать с простейших из числа звеньев, наиболее удаленных от входного звена. Простейшие структурные группы включают два звена и три кинематические пары (группы II класса)

[2, с. 57, 58]. Отдельные из них изображены на иллюстрации.

С C C

D D

D B B

В

Рис.1.3

Анализ структуры механизма рекомендуется проводить путем определения структурных характеристик в следующемпорядке:

1) установить тип структурной схемы;

2) определить число степеней свободы механизма;

3) выделить структурные группы, установить их класс.

Пример определения структурных характеристик рычажного механизма приведен ниже в разделе "Решение тренировочных заданий".

Структурный синтез механизма заключается в проектировании его структурной схемы, которая представляется либо графически, либо аналитически.

При числе звеньев механизма более четырех возникает многовариантность структурных схем, если для синтеза механизма используются структурные формулы. В этом случае находят структурные группы, группы Ассура и

строят структурную схему проектируемого механизма наслоением этих структурных групп. Пример структурного синтеза механизма приведен в [1,с. 26-31].

1.4. Кинематический анализ механизмов с низшими парами

Рассмотрим последовательность определения кинематических характеристик на примере рычажных механизмов.

Метод графоаналитического исследования рычажных механизмов заключается в следующем:

- строят план механизма для принятого положе­ния входного звена в выбранном масштабе;

- выделяют структурные группы;

- определяют вектор скорости кинематичес­кой пары входного звена, вектор изображают графически в выб­ранном масштабе;

- запи­сывают векторные уравнения скорости внутренней кинематичес­кой пары структурной группы, присоединяемой к входному звену. Уравнения составляют для точки принадлежащей как одному, так и другому звену группы. Систему уравнений решают графически (см. рис.2.1).

Аналогично рассматривают другие структурные группы ме­ханизма в порядке их присоединения к входному звену. Графическое построение,

полученное в результате решения системы векторных уравнений называется планом скоростей.

Аналогично строят план ускорений. Отличие состоит в необходимости учитывать касательную и нормальную составляющие ускорения.

C

В С B B

Þ c

1- 1- w₁ V_cв V_c

w₁

А D A D b P,a,d

V_B = w₁ l₁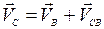

m_V = .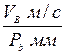

^ BA

Рис. 1.4

Графический метод исследования рычажного механизма заклю­чается в следующем:

- строят планы механизма для ряда положений входного звена;

- строит график перемещения выходного звена в функции координаты входного звена;

- график скорости звена получают графическим диф­ференцированием графика перемещений, график ускорения - графичес­ким дифференцированием графика скорости.

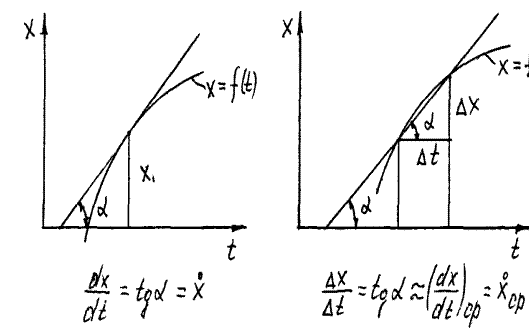
Физический смысл графического дифференцирования: производ­ная функции численно равна тангенсу угла наклона касательной к графику функции с осью абсцисс (рис.1.5.а).

Вместо касательной можно провести секущую (рис.1.5.б). В этом случае тангенс угла наклона хорды будет соответствовать среднему значению производной на интервале Dt. Разбив гра­фик перемещения x = f(t)на интервалы и определив для этих интервалов xср можно построить график xср = f(t).

При графическом дифференцировании следует учитывать мас­штаб по осям абсцисс и ординат:

ср = tg a mt /mx.

(t)

а) б)

Рис.1.5

1.5. Силовой анализ механизмов

Задачей силового анализа является решение первой задачи динамики. Внешние силы, приложенные к звеньям заданы. Необходимо определить реакции связей (реакции в КП механизма).

Для решения этой задачи применяют принцип Даламбера. Принцип заключается в следующем: если к системе внешних сил, действу­ющих на механизм, присоединить силы инерции звеньев, то полу­ченная система сил будет уравновешенной. При этом задача решается методами статики, используя уравнения равновесия (уравнения кинетостатики).

SF^е_k + SF^и_i = 0,

где SF^e_k - внешние силы;

SFⁿ_i - силы инерции.

Система уравнений равновесия может быть решена аналитическим или графоаналитическим методами.

При расчете сил, действующих на звенья механизмов, используют свойства структурных групп – их статическую определимость. Механизм раскладывают на структурные группы, составляя для каждой такой группы уравнение равновесия по принципу Даламбера.

При графоаналитическом методе исследование начинают со структурной группы, включающей выходное звено. Заканчивают анализ определением сил, действующих на входное звено механизма. При выделении группы или отдельного звена действие отсоеди­ненной части механизма заменяют соответствующими реакциями.

При плоскопараллельном движении инерционные силы, распределенные по звену, приводятся к главному вектору силы инерции , приложенной в центре масс тела - точке S и главному моменту сил инерции , определяемые по выражениям:

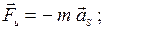
где m - масса тела, a_S - ускорение центра масс, e - угловое уско­рение; Js - момент инерции тела относительно центра масс.

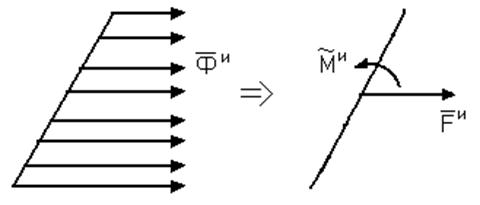
Рис.1.6

При силовом исследовании графоаналитическими методами заменяют главный вектор силы инерции и главный момент сил инерции одной результирующей силой. Это обеспечи­вают параллельным переносом силы на расстояние h = / (на чертеже расстояние переноса h΄ = h/mL). Направление переноса согласовывают с направлением действия момента сил инерции .

S Þ

S h

Рис.1.7

Реакции в разомкнутых парах структурной группы раскладывают на нормальные Fⁿ_ij и тангенциальные F^τ_ij составляющие. Нормальные направляют вдоль звена, тангенциальные – пер­пендикулярно звену. Тангенциальные составля­ющие определяют из уравнения моментов сил, действующих на звенья, относительно внутренней кинематической пары. Размеры плеч измеряют по чертежу. Нор­мальные составляющие определяют из векторного уравнения равнове­сия системы сил, действующих на структурную группу. Векторное уравнение решают графически построением многоугольника сил (план сил). Неизвестные силы определяют из условия замыка­ния векторного многоугольника (векторный многоугольник уравно­вешенной системы сил замкнут).

В случаях, когда требуется определить лишь уравновешивающую силу (или уравновешивающий момент) на входном звене, удобно пользоваться методом «рычага Жуковского». Рычагом Жуковского называют, повернутый на 90° в любую сторону план скоростей механизма, принимаемый за абсолютно твердое тело. По теореме Н.Е.Жуковского: если к «рычагу» приложить действующие на механизм внешние силы и силы инерции в тех же точках, в которых они действуют на механизм, то рычаг будет находиться в равновесии.

,

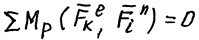где р - полюс плана скоростей;

F^e_k, F^и_i - внешние силы и силы инерции.

1.6. Уравнения движения механизмов

Для исследования движения механизма необходимо знать законы движения начальных звеньев, т.е. зависимости обобщенных координат от времени. Эти зависимости находят из решения обратной (второй) задачи динамики: по заданным силам определить движения.

Силы, действующие на звенья механизма, могут быть функциями времени. Однако, чаще переменные силы, действующие на звенья, связаны с перемещениями или скоростями точки приложения этих сил.

Функциональная зависимость, связывающая величину силы и кинематические параметры (время, координаты и скорость точки приложения силы), называется характеристикой силы.

Считаем, что сила есть функция кинематических параметров. Эти характеристики при динамическом анализе механизмов считаются заданными.

Для определения закона движения начальных звеньев по заданным силам, действующим на звенья механизма, используют уравнения движения механизма. Их число равно числу степеней свободы механизма.

Дата добавления: 2014-12-08