Прикладная механика 2 страница

Уравнения движения механизма представляют в разных формах.

1) Для механизмов с одной степенью свободы одна из наиболее простых форм – на основе теоремы об изменении кинетической энергии. В интегральной форме ее выражение имеет вид:

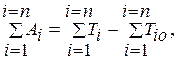
где n – число подвижных звеньев механизма; А_i – работа внешних сил (по отношению механизмов), действующих на звено i на конечном перемещении за заданный промежуток времени; Т_i – кинетическая энергия звена i в конце рассматриваемого промежутка времени; Т_I0 – кинетическая энергия звена i в начале промежутка времени.

Это уравнение можно получить из дифференциальных уравнений движения звеньев путем их интегрирования. Это выражение для механизма получило название: уравнение движения механизма в форме интеграла энергии.

2) Для механизмов с двумя и более степенями свободы более удобны уравнения Лагранжа второго рода.

Уравнения движения механизма при их непосредственном интегрировании являются громоздким даже для плоских механизмов, т.к. необходимо производить суммирование по n -звеньям. Для механизмов с одной степенью свободы получается более простая запись этого уравнения, т.к. все операции å по звеньям выполнены заранее.

Уравнение движения в интегральной форме заменяют тождественным ему уравнением движения первого звена, которое движется так, что его обобщенная координата совпадает в любой момент времени с обобщенной координатой механизма.

Если начальное звено совершает вращательное движение, тогда уравнение движения заменяется тождественным ему уравнением движения одного вращающегося звена – звена приведения. Момент инерции этого звена относительно оси вращения I_п – называют приведенным моментом инерции

Рис.1.8

Если на звено приведения действует пара сил с моментом М_п – приведенный момент сил, расчетная схема называется одномассовой динамической моделью механизма.

Уравнение движения звеньев такой модели в форме интеграла энергии для некоторого промежутка времени, измеряемого при величине угла от j₀ до j, а приведенный момент инерции от I_п до I_п0 имеет вид:

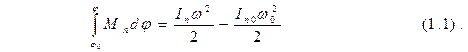Приведенный момент инерции определяют из условия равенства кинетической энергии звена приведенная и кинетической энергии всех звеньев механизма:

Jп w²/2 = S mi V²si /2 + S Jsi w ²i /2,

Jп = S mi (Vsi /w)² + S Jsi (wi /w)² ,

где mi - масса;

Vsi - скорость центра масс;

Jsi - момент инерции относительно центра масс;

wi - угловая скорость i -го звена;

w - угловая скорость звена приведе­ния.

Приведенный момент сил определяют из условия равенства элементарной работы (мощности) приведенного момента и суммы элементарных работ (мощностей) сил и моментов сил, действующих на звенья механизма. При этом звено приведения будет иметь тот же закон движения, что и в составе механизма:

M_п ω = ΣF_k V_k cos (F_k,V_k) + ΣM_iω_i,

M_п = ΣF_k V_k cos(F_k,V_k)/ω + Σm_i ω_i /ω.

При пропорциональном изменении w, wi, Vis, значение приведенных моментов инерции и моментов сил не зависит от скорости звена приведения, а определяется только положением механизма. Поэтому значения приведенных моментов инерции и сил могут быть определены до исследования закона движения звена приведения. При этом они войдут в уравнение движения в виде переменных коэффициентов. Полученное уравнение может быть решено различными методами.

1.7. Решение уравнений движения механизмов

Рассмотрим численное решение уравнений движения механизма при силах, зависящих от положений звеньев.

Задан приведенный момент сил М_п = f(j), обобщенная координата (угол j поворота начального звена). I_п, рассчитывают по формуле

Так же , тогда для определения закона движения начального звена применяется уравнение движения механизма (3.1) в форме интеграла энергии, решаемое с начальными условиями: при t = 0; , .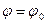

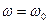Из уравнения получают угловую скорость как функцию угла j:

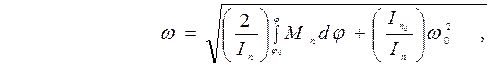
как правило, интеграл в подкоренном выражении решается числовым методом, тогда представляется рядом своих последних значений при изменении j от j₀ до некоторого значения j_m, определяющего конец рассматриваемого этапа движения.

Для определения закона движения начального звена представляем известную функцию в виде: 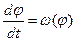, интегрируя, получим:

Это интегрирование осуществляется численным методом. В результате получают функцию t = t(j), зная которую находят искомую функцию: j = j(t).

Для определения углового ускорения начального звена дифференцируют по обобщенной координате j, т.е. определив аналог углового ускорения, находят угловое ускорение:

.

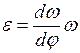Графоаналитическое решение уравнения движения механизма проводят для его установившегося движения при силах, зависимых от положения звеньев.

Характеристики сил известны лишь приближенно, часто задаются в графическом виде, поэтому наряду с аналитическим методом решения уравнения движения применяется комбинированный графоаналитический метод.

Это метод Виттенбауэра, позволяющий наглядно показать, как изменяется угловая скорость начального звена и кинетическая энергия механизма при изменении приведенного момента инерции.

Таким образом, конечным результатом вычислений и построений является график зависимости 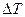от - называемый диаграммой Виттенбауэра.

По ней определяется значение угловой скорости w начального звена в любом положении механизма, если известно значение угловой скорости механизма в начальный момент времени: 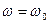при j = 0. Более подробно смотри [1, гл.6].

Далее с учетом коэффициента неравномерности движения механизма определяют момент инерции и конструктивные размеры маховика - детали, позволяющей уменьшить величину коэффициента неравномерности механизма до нормативной величины, стабилизируя в результате работу механизма.

Тесты к разделу "Теория механизмов и машин"

1. Какова степень подвижности шарнирного четырехзвенника, изображенного на рис.

Ответы: 1) 0; 2) 1; 3) 2; 4) (-1).

2. Укажите класс структурной группы, входящей в механизм, схема которого приведена на рис.

Ответы: 1) первый; 2) второй; 3) третий; 4) четвертый.

3. Что не входит в задачу кинематического исследования?

Ответы: 1) определение положений звеньев и траекторий точек;

2) определение линейных скоростей и ускорений точек;

3) определение угловых скоростей и ускорений звеньев;

4) определение размеров звеньев механизма.

4. Какое движение совершает звено 2 на рис.

Ответы: 1) вращательное; 2) плоскопараллельное; 3) колебательное;

4) поступательное.

5.Что такое "m"? (m = 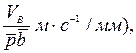где V_B - истинная величина

скорости, м/с; pb - масштабная величина скорости, мм.

Ответы: 1) масштаб длин; 2) масштаб скорости; 3) масштаб ускорения.

6. Число зубьев колес внешней цилиндрической зубчатой передачи равно:

шестерни -10, колеса -15. Чему равно передаточное отношение при ведущей шестерне?

Ответы: 1) 1,5; 2) -2/3; 3) 1,5; 4) 2/3.

7. Какие силы остаются постоянными во всех положениях механизма?

Ответы: 1) силы инерции; 2) силы упругости пружин; 3) силы тяжести; 4) движущие силы.

8. Какие из сил, действующих на механизм, являются внутренними?

Ответы: 1) силы полезного сопротивления; 2) вес звеньев; 3) усилия в кинематических парах; 4) движущие силы.

9. На каком принципе теоретической механики основан кинетостатический расчет механизма?

Ответы: 1) принципе возможных перемещений; 2) принципе Даламбера; 3) принципе сохранения кинетической энергии.

10. К чему приводятся элементарные силы инерции звена, совершающего равномерное вращательное движение вокруг оси, не проходящей через центр тяжести звена?

Ответы: 1) к главному вектору; 2) к главному моменту; 3) к главному вектору и главному моменту.

Вопросы к разделу "Теория механизмов и машин"

1. Назовите основные типы кинематических пар механизмов.

2. По каким признакам классифицируются кинематические пары?

3. Запишите формулы для определения числа степеней свободы плоского и пространственного механизмов, объясните смысл входящих в эти формулы величин.

4. Назовите основные задачи структурного анализа. Дайте определение структурной группы.

5. Укажите основные задачи структурного синтеза. В чем заключается способ синтеза наслоением структурных групп Ассура?

6. Каковы задачи кинематического анализа механизмов?

7. Назовите основные методы кинематического анализа механизмов.

8. Как по уравнениям движения звеньев механизма определяют скорости и ускорения?

9. Как построить диаграмму перемещения звена механизма?

10. Укажите основные задачи динамического анализа.

11. Какие силы называются движущими, какие - силами сопротивления?

12. Как определяются силы и моменты сил инерции, их модуль и на­правление?

13. Перечислите основные задачи силового анализа.

14. Определите суть метода исследования построением плана сил.

Раздел 2. Сопротивление материалов

2.1. Основные понятия и определения

Изделия техники: машины и механизмы, конструкции и сооружения должны удовлетворять требованиям надежности и экономичности при их изготовлении и эксплуатации. Часто выход из строя одной части конструкции или детали механизма приводит к разрушению всего изделия. Поэтому требованиям надежности и экономичности должны удовлетворять отдельные элементы машин, различных конструкций и сооружений, от чего зависит их работоспособность. Это основная цель Сопротивления материалов».

Отдельную часть конструкции, сооружения или деталь машины условимся называть элементом конструкции (ЭК).

Сопротивление материалов (СМ) – наука об инженерных методах расчетов элементов конструкций (ЭК) на прочность, жесткость и устойчивость с целью обеспечения требуемой надежности и экономичности, минимальной материалоёмкости.

Под экономичностью конструкции подразумевается его минимальные материалоёмкость и затраты на изготовление и эксплуатацию.

Надежность конструкции – способность выполнять заданные функции, сохраняя свои нормативные эксплуатационные качества в течение требуемого срока работы.

Основная количественная характеристика надежности - это вероятность безотказной работы конструкции, определяемой требуемым ресурсом.

Прочность – способность конструкции или отдельных ее частей противостоять внешней нагрузке, не разрушаясь. Под внешней нагрузкой подразумевается совокупность внешних сил и моментов, действующих на конструкцию в целом и ее элементы.

Жесткость –способность конструкции или отдельных ее частей противостоять внешней нагрузке от изменения первоначальных форм и размеров.

Количественное выражение изменения формы и размеров ЭК и всей конструкции в целом называется деформацией.

Типы деформаций:

1) с геометрической точки зрения: линейные и угловые;

2) с физической точки зрения: упругие и пластичные (материалы: упругие, пластичные, упруго-пластичные);

3) по условиям нагружения: растяжение-сжатие, сдвиг (срез), кручение и изгиб.

Устойчивость – способность ЭК или конструкции в целом сохранять заданную форму упругого равновесия при внешней нагрузке.

При решении задач сопротивления материалов используются приемы моделирования. От правильности выбора критериев моделирования в конечном итоге зависят правильность и точность расчетов.

Элементы конструкций условно рассматриваются как модели (расчетные схемы).

Совокупность свойств расчётной модели (схемы) называют моделью прочностной надёжности. Эти свойства даны в таблице 2.1.

Таблица 2.1.

МАТЕРИАЛ ОДНОРОДНЫЙ, СПЛОШНОЙ, УПРУГИЙ, ИЗОТРОПНЫЙ

МОДЕЛЬ РАЗРУШЕНИЯ

1.СТАТИЧЕСКОЕ 2.МАЛОЦИКЛОВОЕ 3.УСТАЛОСТНОЕ 4.ПОД ДЕЙСТВИЕМ УДАРНЫХ И ИНЕРЦИОННЫХ НАГРУЗОК

НАГРУЗКИ: ОБЪЕМ- НЫЕ И ПОВЕРХНОСТНЫЕ, СОСРЕДОТОЧЕН- НЫЕ, СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ, ОТ ВОЗДЕЙСТВИЯ СИЛ ТЯЖЕСТИ

1. БРУС: СТЕРЖЕНЬ, ВАЛ, БАЛКА 2. ОБОЛОЧКА 3. ПЛАСТИНА 4. МАССИВНОЕ ТЕЛО

МОДЕЛЬ НАГРУЗКИ (СИСТЕМЫ ВНЕШНИХ И ВНУТРЕННИХ СИЛ)

МОДЕЛЬ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ

МОДЕЛЬ МАТЕРИАЛА

МОДЕЛЬ ПРОЧНОСТНОЙ НАДЕЖНОСТИ

В качестве конструкционных материалов в машиностроении используются в основном металлы и их сплавы, а также различные органические и неорганические материалы (полимеры, пластмассы, керамика, композитные материалы).

В сопротивлении материалов используются гипотезы о том, что материалы имеют сплошную однородную среду. Материал считается изотропным, т.е. свойства его по любым направлениям одинаковы. Считается, что материалы, абсолютно упругие и деформируемые, подчинятся закону Гука. Деформации малы в сравнении с первоначальными размерами ЭК, то есть должны выполняться принцип неизменности первоначальных размеров и должен принцип независимости действия сил.

Геометрическая форма элементов конструкций часто бывает весьма сложной. Для определения напряженного и деформационного состояния применяют упрощенные схематизированные модели формы элементов конструкций с помощью стандартных типовых форм. Основными моделями формы являются брусья, пластины, оболочки, массивные тела.

Брус – геометрическое тело, у которого размеры сечения значительно меньше длины. Сечение, перпендикулярное оси бруса, называется поперечным сечением.

Линия, проходящая через центры тяжести поперечных сечений, называется осью бруса.

Брус, работающий на растяжение-сжатие, называют стержнем.

Брус, работающий на кручение, называют валом. В машинах и механизмах валы, в основном, работают при совместном действии изгиба и кручения. Брус, работающий на изгиб, называется балкой. Так как размеры сечения бруса (b и h) значительно меньше длины (l), в расчетных моделях брусья (валы, балки) изображают в виде сплошных линий, совпадающих с их осями. Брус – основной объект расчёта в сопротивлении материалов.

При деформировании используется гипотеза плоских сечений: сечения плоские до деформации остаются плоскими после деформации (гипотеза Бернулли).

Оболочками называются геометрические формы, ограниченные двумя близкими поверхностями.

Пластины ограничиваются двумя плоскими или слабоизогнутыми поверхностями (крыши зданий, палубы судов, люки и т.п.)

Массивное тело (массив) – модель элемента конструкции, в котором все размеры соизмеримы и являются величиной одного и того же порядка.

Реальные детали машин со сложной геометрией можно рассматривать как сочетание простых моделей формы.

Как известно, сила – мера механического взаимодействия тел. Если конструкцию или ЭК рассматривать изолировано от взаимодействующих с ними тел, действие последних заменяется силами, которые называются внешними силами. Внешние силы деформируют тело. Внешние силы, действующие на элемент конструкции, подразделяют на три группы (рис.2.1):

1. Сосредоточенные силы (F) – силы, действующие на небольших участках поверхности детали или элемента конструкции (рис.2.1-а, в).

2. Распределенные силы (q _1,2) – силы, действующие на значительных участках поверхности (рис.2.1-а).

3. Объемные или массовые силы – например, силы тяжести, инерции, электромагнитного притяжения (рис. 2.1-б).

Совокупность внешних сил, действующих на твёрдое тело, называют нагрузкой.

Возможно изменение сил во времени, определяемое условиями эксплуатации и параметрами рабочего процесса изделия: цикличность нагрузки, внезапные удары, имеющие вероятностный характер, вибрации. По характеру длительности действия принято различать нагрузки статические и динамические.

Статическая нагрузка – нагрузка, не изменяющаяся с течением времени (собственный вес конструкции) или изменяющаяся медленно, так что эффектом ускорения можно пренебречь.

Динамическая нагрузка – это нагрузка, учитывающая ускорения взаимодействующих тел. Динамическая нагрузка в отличие от статической меняет свое значение, положение или направление в короткие промежутки времени (движущие нагрузки, ударные, сейсмические и др.), вызывая большие ускорения и силы инерции, что приводит к определенному характеру деформирования и к колебаниям конструкций и сооружений. Динамические нагрузки делят на ударные, повторно-переменные и инерционные. Динамические нагрузки являются функцией времени.

Ударная нагрузка в момент ее приложения обладает определенной кинетической энергией.

Повторно-переменные нагрузки – нагрузки, которые во времени изменяются циклически (например, при вращении валов возникает совместное переменное действие изгиба и кручения).

а)	б)
в)

Рис.2.1.

а) нагрузки, действующие на твердое тело:

q ₁ – нагрузка, распределенная по линии (Н/м);

q ₂ – нагрузка, распределенная по площади (Н/м²);

F ₁, F ₂ – сосредоточенные силы (Н).

б) нагрузка, распределенная по объему тела Н/м³, G – сила веса;

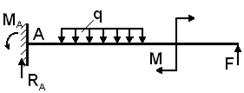
в) нагрузка, действующая по длине балки

- активные силы:

q – распределенная нагрузка,

М – сосредоточенный момент (Нм),

F – сосредоточенная сила (Н)

- реактивные силы:

R_А – опорная реакция (Н),

М_А – реактивный момент (Нм).

Процесс разрушения сопровождается упругой и пластической деформациями. Различают следующие модели разрушений в зависимости от условий нагружения и вида деформирования.

Статическое разрушение -пластическая деформация развивается при постоянной нагрузке. Характер разрушения – пластический (со значительной остаточной деформацией) или хрупкий (с малой остаточной деформацией).

Длительное статическое разрушение – при значительных температурах развивается ползучесть, пластические деформации увеличиваются с течением времени при постоянной нагрузке, что приводит к разрушению.

Усталостное разрушение - наступает после многократных циклически изменяющихся, нагрузках. Разрушение происходит при отсутствии видимых пластических деформаций. При этом разрушение происходит в том месте детали, где имеется концентратор напряжений, появляется трещина и распространяется по объему материала.

Малоцикловое разрушение – разрушение, которое носит смешанный пластический и хрупкий характер.

2.2. Метод сечений. Виды деформаций

При деформировании упругих тел под действием внешней нагрузки возникают силы противодействия деформированию - внутренние силы. Пока не произойдет разрушение тела, внешние силы уравновешиваются внутренними. Природа внутренних сил – атомарное и молекулярное взаимодействие частиц тела. Внутренние силы или внутренние силовые факторы (ВСФ) определяются методом сечений.

Сущность метода сечений: упругое твердое тело, несущее внешнюю нагрузку, уравновешиваемую телом, мысленно рассекается плоскостью. Если тело – брус и секущая плоскость проводится перпендикулярно его оси, получают поперечное сечение.

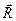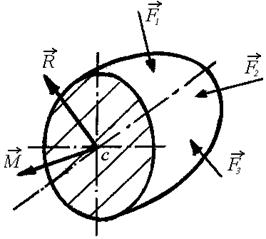
Затем рассматривается условие равновесия каждой отсеченной части, то есть определяются сила и момент, которые, будучи приложенными в центре тяжести сечения, уравновесят внешнюю нагрузку, действующую на рассматриваемую отсеченную часть. Эта сила и момент, приложенные в центре тяжести сечения, являются соответственно главным вектором и главным моментом внутренних сил - 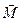(рис. 2.2-б).

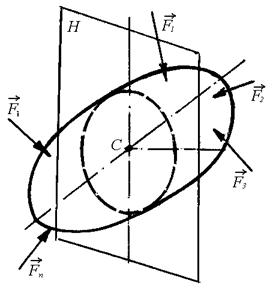
На рис.2.2 (а, б, в) показана последовательность определения ВСФ по методу сечений.

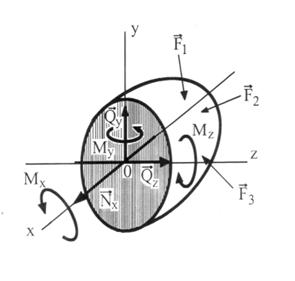
Через центр тяжести сечения проводят три взаимно перпендикулярные оси. При этом ось х перпендикулярна сечению, а оси y и z проходят по поверхности сечения, совпадая с его главными осями. Определяют составляющие главных вектора 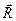и момента 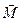относительно осей x, y, z. (рис.2.2-в)

N_x - сила, перпендикулярная сечению, Q_y и Q_z – силы, действующие по поверхности сечения, M_x, M_y, M_z – моменты относительно соответствующих осей (рис. 2.2-в). Таким образом, в общем случае в сечении тела действуют шесть внутренних силовых факторов, величины и направление которых можно определить с помощью шести уравнений статики для пространственной системы сил:

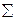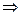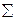(определяется) N_x; m_x = 0 (определяется) M_x; (определяется) Q_y; m_y = 0 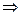(определяется) M_y;

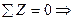(определяется) Q_z; 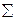m_z = 0 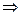(определяется) M_z;

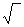N_x² + Q_x² + Q_z² = 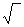М_x² + М_y² + М_z²

а)	б)
в)	H – секущая плоскость; С – центр тяжести сечения; Силы Fί действуют на одну сторону сечения ί = 1,2,...,n → R - главный вектор внутренних сил; → n → R = ∑ Fί ^ί^=1 → M - главный момент внутренних сил. → → → M = ∑ M ί (Fί) 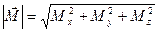Nx, Qy, Qz, Mx, My, Mz – внутренние силовые факторы.

Рис.2.2

Напряжение – мера интенсивности внутренних сил, распределенных в сечении деформируемого тела по определенному закону.

Оптимальная величина напряжений – основной критерий прочности материала.

Единица измерения напряжения – мегапаскаль (МПа)

1 МПа = 1 Н/мм²

Под действием различных силовых факторов тела могут испытывать различные типы деформаций.

Дата добавления: 2014-12-08