Прикладная механика 4 страница

Заклепки работают на смятие и срез. Условие прочности на срез: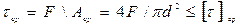

Условие прочности на смятие имеет вид:

,

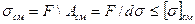где d - диаметр заклепки, s - толщина листа.

Резьбовые соединения являются наиболее распространенными среди разъемных соединений. Это соединения деталей с помощью различных резьб и резьбовых крепежных элементов. Они обладают высокой несущей способностью и надежностью. Резьбовые соединения позволяют применять однотипные стандартные детали в различных машинах. Но их существенным недостатком является концентрация напряжений в резьбе, снижающая сопротивление циклическим нагрузкам.

Цилиндрическая резьба широко применяется в соединениях деталей ихарактеризуется следующими параметрами: формой и размером профиля; наружным, внутренним и средним диаметрами; шагом; числом заходов.

Профилем называют контур сечения резьбы плоскостью, проходящей через ее ось. По виду профиля различают резьбы метрические; дюймовые; трубные (мелкие дюймовые); трапецеидальные; круглые и квадратные (рис. 3.3). Стандартизованы параметры всех резьб, кроме квадратной. Профиль резьбы характеризуется углом (a), теоретической (H) и рабочей высотами (h).

Основные размеры резьбы: наружный диаметр (d), внутренний диаметр (d₁), средний диаметр (d₂),шаг р – расстояние между одноименными точками профиля соседних витков в осевом направлении (рис. 3.3). Резьбы выполняют одно-, двух-, и многозаходными. Ход резьбы t определяется перемещением инструмента при ее изготовлении в осевом направлении за один оборот заготовки. Пусть число заходов равно (а), тогда ход резьбы составит

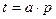
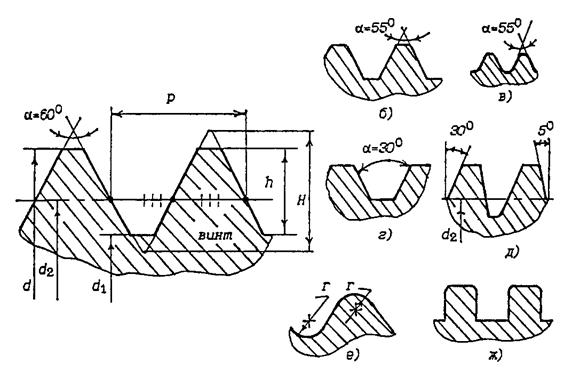Рис. 3.3. Профили и параметры резьб

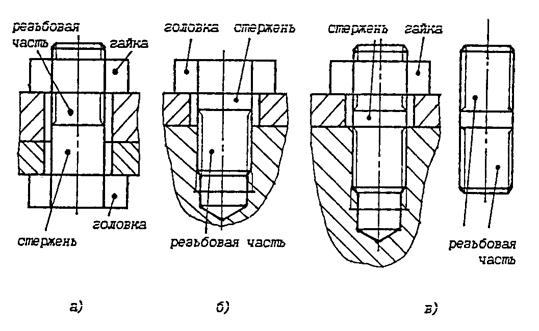
К резьбовым элементам крепежа относятся болты, винты, шпильки, гайки и резьбовые вставки (рис. 3.4).

Болтовые соединения (рис. 3.4) используются для соединения деталей относительно небольшой толщины при наличии места для гайки и головки Если данные условия не выполняются, но в одной из деталей можно высверлить резьбовые отверстия, используют винтовые соединения (рис. 3.4).

В случае необходимости частой сборки-разборки подобного вида соединений, вызывающей изнашивание резьбовых отверстий в детали, вместо винтовых применяют шпилечные соединения (рис. 3.4) или в резьбовые отверстия вкручивают резьбовые вставки, которые представляют собой втулки из износостойких материалов с наружной и внутренней резьбой. Шпилечные соединения или резьбовые вставки используют, когда материал детали с резьбовым отверстием не обладает высокой твердостью (легкие сплавы, пластмассы).

Расчет резьбы на прочность. Наибольшую опасность для крепежных резьб представляет срез витков. Если развернуть виток резьбы винта (гайки) на плоскость по диаметру d₁(d), опасное сечение будет представлять собой прямоугольник со сторонами а_ср и pd₁(pd). Проверочный расчет витков резьбы на срез винта и гайки –

,

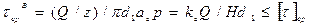
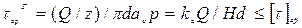где Q - осевая нагрузка на резьбу; z и p - число витков и шаг резьбы; k_c– коэффициент, определяющий полноту профиля резьбы (для метрических резьб k_c= 0,87); H – высота гайки.

Шпоночные и шлицевые (зубчатые) также относятся к разъемным соединениям. Они предназначены для передачи вращательного движения и крутящего момента от валов к присоединенным деталям и наоборот.

Шпоночные соединения просты и надежны, технологичны, обеспечивают относительное удобство сборки-разборки. Их недостатком является наличие у валов и ступиц шпоночных пазов, ослабляющих сечения соединяемых деталей и вызывающих значительную концентрацию напряжений, что понижает сопротивление валов усталости.

По конструкции шпонки подразделяются на призматические, сегментные, клиновые. Геометрические размеры первых двух типов шпонок стандартизованы. Наибольшее распространение получили призматические шпонки.

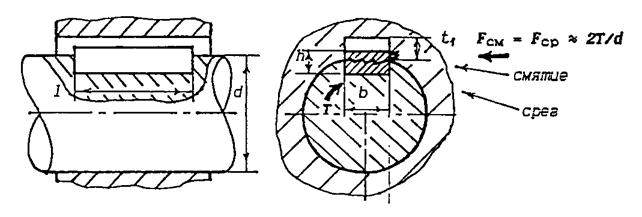Рабочими поверхностями призматических шпонок являются боковые грани. Шпонки работают на смятие и срез (рис.3.5).

Рис. 3.5. Соединение призматической шпонкой

Условие прочности на срез –

,

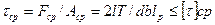где Т – передаваемый крутящий момент.

Условие прочности при смятии -

.

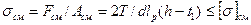Допускаемые напряжения [s]_см выбирают в зависимости от материалов

соединяемых деталей и шпонок. Для стальных валов, ступиц и шпонок принимают [s]_см = 120…180 МПа.

Соединения сегментными шпонками, представляющими собой пластины

в форме части диска по принципу работы и расчета аналогичны соединениям призматическими шпонками. По сравнению с ними они более технологичны, но значительнее ослабляют валы.

Шлицевые соединения образуются при вхождении выступов (зубьев) на

валах в соответствующие впадины (пазы) на ступицах. Шлицы выполняют прямобочного, эвольвентного и треугольного профилей (рис. 3.6). Параметры шлицевых соединений стандартизованы (кроме соединений с зубьями треугольного профиля).

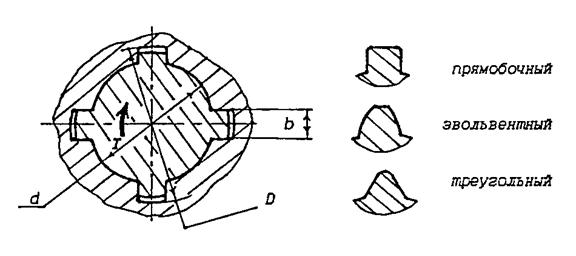
Рис. 3.6. Шлицевые соединения.

Шлицевые соединения имеют большие, чем шпоночные: нагрузочную

способность, сопротивление валов усталости, технологичность и точность.

Для шлицевых соединений прямобочного профиля применяют три вида центрирования: по боковым граням (обеспечивающее наибольшую нагрузочную способность); по наружному диаметру D (для ступицы малой твердости); по внутреннему диаметру d.

Шлицевые соединения проверяют на смятие по условию прочности вида

,

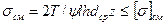где y - коэффициент неравномерности распределения нагрузки между шлицами; l – длина поверхностей контакта зубьев на валу с пазами в ступице; h – высота данных поверхностей; d_cp – их средний диаметр; z – количество зубьев.

3.3. Механические передачи

Передачами в машинах называют устройства, передающие энергию механического движения на расстояние, преобразующие его параметры и вид. Современные технологические машины в пищевой промышленности и в других отраслях проектируют и создают по схеме: энергетическая машина, передаточный механизм, исполнительный орган машины, система управления.

Устройство, состоящее из двигателя, передаточных механизмов и системы управления для приведения в движение машин и механизмов называется приводом.

Ключевым звеном привода является передача. Угловые скорости двигателя w_дв и рабочего органа машины w_ром, как правило, не равны. Для их согласования применяют механическую передачу. Наиболее широкое распространение в технике получили передачи вращательного движения. Они используются как для понижения (редукции), так и для повышения угловой скорости двигателя до заданной угловой скорости исполнительного звена машины. В зубчатых передачах первые механизмы, называют редукторами, а вторые – мультипликаторами.

По способу передачи движения от ведущего вала к ведомому различаются передачи трением и зацеплением; непосредственного касания (фрикционные, зубчатые, червячные, волновые, винтовые) и с гибкой связью (ременные, зубчато-ременные, цепные); по назначению – кинематические и силовые; по взаимному расположению валов в пространстве – между параллельными, пересекающимися, перекрещивающимися и соосными осями валов.

Рассмотрим кинематические и силовые соотношения в передачах.

Основные параметры передачи следующие: мощность Р (кВт); быстроходность, выражаемая угловой скоростью w (с^-1) или частотой вращения n (мин^-1); вращающий момент Т (Н×м); коэффициент полезного действия (КПД) h и передаточное число и.

Важнейшей характеристикой любой механической передачи является передаточное число, показывающее, во сколько раз быстроходность входного звена 1 отличается от аналогичного параметра выходного звена 2:

,

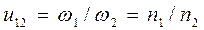где w = pn / 30.

При этом значение 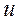> 1 и такие передачи называют понижающими, процесс преобразования частоты вращения – редуцированием, а передачу, выполненную в закрытом корпусе – редуктором.

Передаточное число можно выразить через диаметры, или число зубьев, тогда формула будет иметь вид:

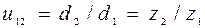
Привод может включать несколько передаточных механизмов (ступеней). При этом значение общего передаточного числа определяется произведением передаточных отношений отдельных кинематических ступеней привода

При разбивке общего передаточного числа следует руководствоваться кинематическими возможностями отдельных передач. Передаточные числа редукторов следует принимать стандартными.

При передаче движения часть мощности теряется, например на трение. Эти потери выражаются коэффициентом полезного действия:

h = Р₂ / Р₁

Окружная сила передачи F (Н):

F_t = P / u = 2T /d,

где Р – мощность (Вт), окружная скорость u ведущего или ведомого звена (м/с), d – диаметр шкива, колеса, звездочки, червяка (мм).

Выражение вращающего момента Т (Н×м):

Т = Р / w

Требуемая мощность электродвигателя Р_ЭД (кВт):

Р_ЭД = Р_Т / h_общ,

где Р_Т – сила на исполнительном звене машины; h_общ – общий КПД привода, равный произведению частных КПД отдельных передач, составляющих привод:

h_общ = h₁₂×h₂₃…h_n.

Зубчатые передачи предназначены для передачи и преобразования вращательного движения с изменением угловых скоростей и крутящих моментов посредством зубчатого зацепления. Наибольшее распространение получили передачи с эвольвентным профилем зуба.

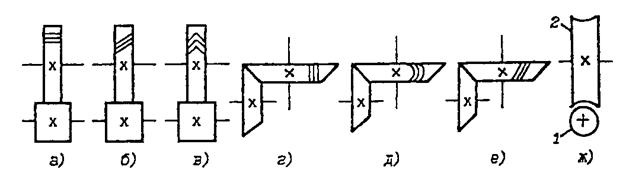
Зубчатые передачи между параллельными валами осуществляются с помощью цилиндрических зубчатых колес, образующие венцов которых параллельны осям валов. Наиболее широкое применение в технике нашли цилиндрические зубчатые колеса с прямыми, косыми и шевронными зубьями (рис. 3.7 а,б,в).

Рис. 3.7. Схемы зубчатых передач

Если оси валов пересекаются, для передачи используются конические зубчатые колеса с прямыми, круговыми (рис. 3.7.г.д. ) и косыми (рис. 3.9.е) зубьями. Когда оси валов перекрещиваются, применяются комбинированные зубчато-винтовые передачи, наиболее распространенным видом которых является червячная, состоящая из ведущего червяка 1, представляющего собой силовой винт, и ведомого червячного колеса 2 (рис. 3.7.ж).

По сравнению с другими механическими передачами зубчатые обладают следующими преимуществами:

- относительно малыми габаритами и высокими (до 0,985) КПД;

- сравнительно большой долговечностью и надежностью в работе;

- постоянством передаточного отношения;

- возможностью применения для широкого диапазона крутящих моментов, угловых скоростей и передаточных чисел.

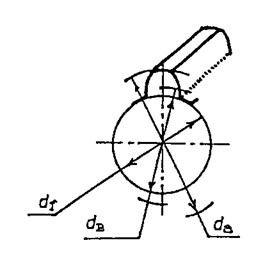
Цилиндрические зубчатые передачи. Зубчатые венцы колес ограничены поверхностями вершин зубьев диаметром d_а и впадин диаметром d_f.

Рис. 3.8. Зубчатый венец колеса

Каждое зубчатое колесо характеризуется числом зубьев z и диаметром делительной окружности d_d (рис. 3.8):

,

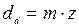где 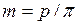- модуль зацеления. Здесь р - шаг зубьев измеренный по делительной окружности.

Колесо меньшего диаметра называется шестерней (индекс параметров -1), а большего – колесом (2). Делительная окружность делит зуб колеса на головку и ножку (высотой h_a и h_f соответственно). Модуль m характеризует зацепление колес, имеет размерность длины [мм] и стандартные значения. Модуль определяет геометрические параметры зубчатого колеса.

- диаметр вершин зубьев d_a = d_w + 2h_a = d_w + 2m;

- диаметр впадин венца d_f = d_w – 2h_f = d_w – 2,5m.

Материалы для изготовления зубчатых колес выбирают в зависимости от требований, предъявляемых к размерам и массе передачи, а также в зависимо-сти от мощности, окружной скорости и требуемой точности изготовления колес и их стоимости. В качестве материалов для зубчатых колес применяют стали, чугуны и пластмассы.

Силы в зацеплении. Нормальная сила F_n направлена по линии зацепления, которая является общей нормалью к активным поверхностям зубьев. Силы, действующие в зацеплении, обычно приложены в полюсе зацепления (рис. 3.9). Раскладываем нормальную силу на окружную F_t и радиальную F_r. По заданным T₁ и d₁ определяют 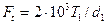и через нее выражают F_r и F_n:

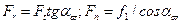
Такое разложение удобно для расчетов зубьев, валов и опор.

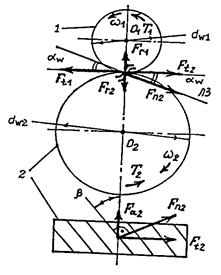
Рис. 3.9. Силы в зацеплении

Расчет всех зубчатых передач проводят по контактным напряжениям и на изгиб (см. более подробно [1-3]).

Образующие боковых поверхностей зубьев косозубых цилиндрических колес наклонены к осям колес на некоторый угол b (для большинства подобных передач b = 8…15⁰ , (рис.3.9). Благодаря этому косозубые передачи имеют ряд преимуществ (по сравнению с прямозубыми):

- позволяют передавать большую нагрузку при тех же габаритах;

- работают более плавно и с меньшими шумами;

- лучше прирабатываются.

Расчет параметров косозубых цилиндрических передач аналогичен расчету характеристик прямозубых, но обладает рядом особенностей. Косозубые колеса имеют два шага по начальной окружности: нормальный р_n (в направлении, перпендикулярном образующим боковых поверхностей зубьев) и торцевой р_t (по ободу колеса). Косозубые колеса характеризуются также и двумя модулями – нормальным m_n = p_n/p и торцевым m_t = p_t/p.

Очевидно, что – р_t = p_n/cosb,

тогда – m_t = m_n/cos b.

Пусть число зубьев косозубого колеса равно z. Диаметр начальной окружности – .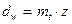

Учитывая предыдущее выражение получим –

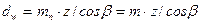
где m = m_n – модуль инструмента для нарезания зубчатого венца.

Межосевое расстояние – .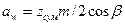

При проектировании косозубых передач межосевое расстояние принимают по размерам стандартногоряда и используют для выбора модуля условие m £ 0,02a_w. Суммарное количество зубьев

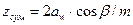
Угол наклона зубьев .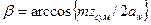

Силы в зацеплении:

Окружная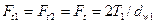

Осевая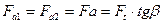

Радиальная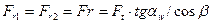

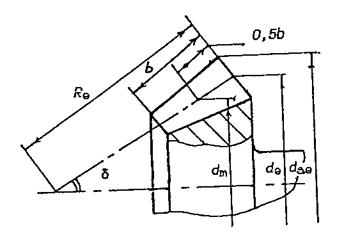
Конические зубчатые передачи позволяют преобразовывать и передавать вращательное движение между валами, оси которых пересекаются под каким-либо углом. Наибольшее распространение в технике получили прямозубые конические передачи. Они характеризуются следующими геометрическими параметрами (рис. 3.10): диаметрами d_m (средний диаметр), d_ae, d_e, углом d, равным половине угла при вершине конуса элемента передачи и конусным расстоянием R_e.

Рис. 3.10. Параметры прямозубого конического колеса

При расчетах конических колес округлять величину модуля до стандартного значения необязательно. Диаметры поверхностей выступов и впадин рабочего венца конического колеса с равновысокими зубьями –

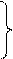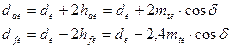
Передаточное число –

.

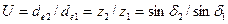Конусное расстояние - ,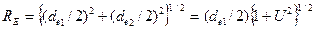

а модуль выбирают из условия –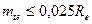

Силы в зацеплении:

Тангенциальная сила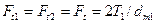

Радиальная сила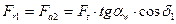

Осевая сила .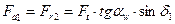

Червячные передачи применяются для преобразования и передачи вращательного движения между валами, оси которых перекрещиваются, как правило, под прямым углом.

Червячные передачи являются зубчато – винтовыми. Червячная пара состоит из червяка 1 и червячного колеса 2 (рис.3.11). При этом в большинстве случаев ее ведущим звеном служит червяк.

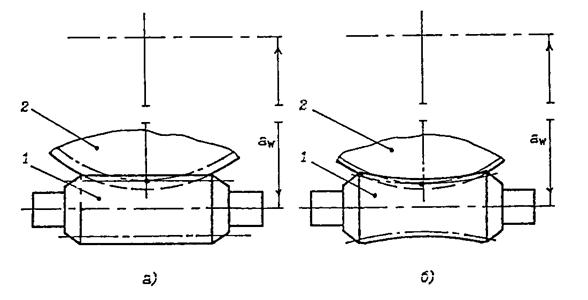
Рис.3.11. Схемы червячных передач

К преимуществам таких передач следует отнести возможность получения большого передаточного числа (до 80) на одной ступени, а также плавность и бесшумность работы. Существенными недостатками червячных передач являются сравнительно низкий КПД (h = 0,65…0,91), значительное выделение теплоты в зоне контакта червяка с колесом, интенсивное изнашивание и склонность к заеданию, что обусловливает необходимость применения при изготовлении червячных колес дорогих антифрикционных материалов.

Червячные передачи используют при небольших и средних (до 50 кВт) мощностях. Червячные колеса изготавливают из обладающих антифрикционными свойствами латуней и бронз. В тихоходных передачах допустимо применение колес из относительно мягких серых чугунов.

Червяки, представляющие собой силовые винты, выполняют, какправило, из цементированных и среднеуглеродистых сталейс поверхностной объемной закалкой. Червяки изготавливают одно- и многозаходные (стандартное число заходов червяка z₁ = 1,2,4). В зависимости от формы внешней образующей червяка различают цилиндрические и глобоидные червячные передачи (см. рис.3.11 а) и б)). В зависимости от формы винтовой поверхности резьбы различают эвольвентные, конволютные и архимедовы цилиндрические червяки.

Профиль эвольвентных червяков в торцевом направлении очерчен эвольвентой окружности. Конволютные червяки имеют прямолинейный профиль в сечении, нормальном к витку.

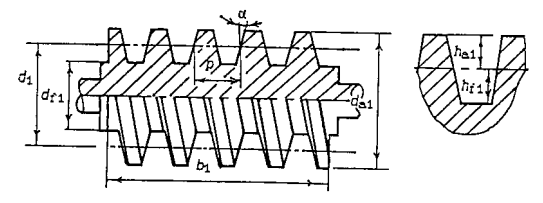
Наибольшее распространение получили архимедовы червяки, в основе осевого профиля которых лежит равнобедренная трапеция с углом a = 20⁰. В торцевом сечении их витки ограничены архимедовой спиралью (рис. 3.12). Архимедовы червяки подобны ходовым винтам с трапецеидальной резьбой.

Рис. 3.12. Архимедов червяк и его параметры

Параметры червячных передач. Основным геометрическим параметром червячной передачи являются осевой модуль червяка m, равный торцевому модулю червячного колеса. Модули червячных передач стандартизированы.

Геометрические размеры элементов червячной передачи (рис. 3.13):

- делительный диаметр червяка-

,

где q – коэффициент диаметра червяка (величина стандартная).

- делительный диаметр колеса –

,

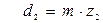
где z₂ – число зубьев колеса;

- высота ножки витка червяка и зуба колеса-

,

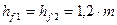- высота головки витка червяка и зуба колеса-

;

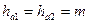- диаметр вершин витков червяка-

;

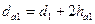- диаметр вершин зубьев колеса-

;

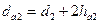- диаметр впадин червяка-
;

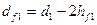- диаметр впадин колеса-

;

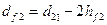- межосевое расстояние-

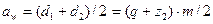
Значения длины нарезной части червяка b₁ и ширины колeса b₂ принимаются конструктивно в зависимости от числа заходов червяка.

Передаточное число червячных пар

.

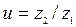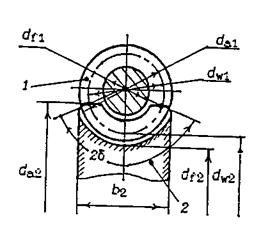
Рис. 3.13. Геометрические параметры червячной пары

Силы в зацеплении. Окружная сила на червяке F_f1 равна осевой силе на червячным колесе:

,

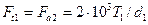где Т₁ - вращающий момент на червяке; d₁- делительный диаметр червяка.

Радиальная сила на червяке F_r1 равна радиальной силе на колесе F_r2:

F_r1= F_r2= F_r1tga.

Осевая сила на червяке F_a1 равна окружной силе F_t2 на червячном колесе:

,

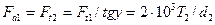где Т₂ – вращающий момент на червяке; d₂ – длительный диаметр червяка.

3.4. Валы, оси и опоры

Валы и оси предназначены для поддерживания вращающихся элементов машин – зубчатых колес, шкивов, звездочек и т.д. Конструктивно оси и прямые валы, представляющие собой детали цилиндрический формы (иногда с коническими участками), различаются мало.

Характер работы валов и осей принципиально различен: оси воспринимают только изгибающие нагрузки, а валы работают на кручение и изгиб, передавая полезные крутящие моменты. Силовые факторы, действующие на оси и валы, передаются на корпуса и станины машин через опоры (например, подшипники).

Оси могут быть неподвижными или вращающимися совместно с насаженными на них деталями. Валы при работе машины вращаются всегда.

В зависимости от геометрической формы различают прямые, колончатые и гибкие валы. По конструктивному исполнению оси и валы бывают постоянного и ступенчато-переменного сечения (чаще всего кругового), сплошные полные.

Подвижные и неподвижные оси работают на изгиб. Условие прочности имеет вид –

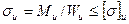
где М_и – изгибающий момент, в опасном сечении оси, W_и – момент сопротивления опасного сечения изгибу, [s]_и - допускаемое напряжение изгиба.

Для осей кругового поперечного сечения

W_и = p×d³/32,

где d – диаметр оси.

Как правило, проектирование валов включает три этапа:

- ориентировочный расчет (на кручение);

- эскизная проработка (компоновка) конструкции;

- проверочный расчет на выносливость (циклическую прочность).

Суть ориентировочного или проектного расчета состоит в определении

диаметра вала в опасном сечении из условия прочности на кручение. Напряжения изгиба, зависящие от геометрии вала, пока не известны и учитываются косвенно, занижая допускаемые напряжения [t]_кр в 1,5…3 раза. Таким образом, условие прочности для вала в данном случае имеет вид -

t_кр = Т/W_кр £ [t]_кр/(1,5…3),

где Т = Р/w - крутящий момент на валу (Р- передаваемая мощность, w - угловая скорость вала), а W_кр - момент сопротивления сечения кручению (для сплошных валов кругового поперечного сечения):

W_кр = p×d³/16.

При проектном расчете диаметр вала d определяется из соотношения -

.

Полученное значение диаметра, как правило, округляют до ближайшего стандартного размера.

На следующем этапе производят эскизную проработку конструктивной схемы вала. На этой стадии проектирования предварительно определяется геометрия вала.

Проработка эскизного проекта позволяет перейти к проверочному расчету вала. Суть проверочного расчета вала на выносливость (усталость) состоит в определении коэффициентов запаса прочности n_i в опасных сечениях, величины которых сравнивают с допускаемыми значениями [n]. Более подробно о проверочном расчете валов см. [ 3,5].

Опоры различают двух типов: поступательного (направляющие) и вращательного (подшипники) движения. По виду трения их разделяют на подшипники скольжения и качения.

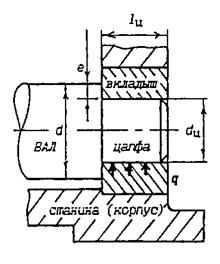
В технике чаще используют подшипники качения, поскольку потери на трение в подобных опорах существенно меньше. Подшипники скольжения применяют при стесненных межосевых габаритах и в ряде машин специального назначения, выпускаемых в единичных экземплярах. Подшипник скольжения состоит из корпуса, шейки вала и вкладыша, выполняемого из антифрикционного материала (рис. 3.14).

Рис. 3.14. Схема подшипника скольжения

Расчет цапфы на нагрев. Поскольку тепловыделение в данном случае характеризуется давлением (q) в зоне контакта и скоростью относительного перемещения взаимодействующих деталей, расчет производят по выражению:

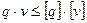
где v – окружная скорость вала; [q] - допускаемое давление в зоне контакта; допускаемая скорость [v] (скорость скольжения в опоре) определяют по справочным данным.

Подшипники качения состоят из наружного и внутреннего колец, тел качения, сепаратора (рис. 3.15). По виду тел качения различают шариковые, роликовые и игольчатые подшипники. В зависимости от характера воспринимаемых нагрузок подшипника качения делятся на радиальные, упорные, радиально-упорные и упорно-радиальные. Все типы подшипников качения стандартизированы.

Дата добавления: 2014-12-08