Решение тренировочных заданий

Задача 1

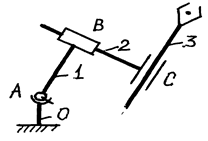
Дана структурная схема механизма рис.4.1

Определить число звеньев механизма, число кинематических пар, тип кинематических пар, класс кинема­тических пар по числу степеней свободы, вычислить степень подвижности механизма.

Решение.

1. Данный механизм содержит непод­вижное звено-стойку "О", под­вижные звенья I, 2, 3, кинемати­ческие пары А, В, С.

2. Характеристики кинематических

пар механизма приведены в нижесле- дующей таблице.

Рис.4.1

Классификация кинематических пар механизма

Обозна- чение пары	Тип пары	Число степеней свободы	Число связей	Класс пары (по степени свободы)
А	Сферическая с пальцем			Р2
В	Поступательная	I		Р1
С	Цилиндрическая			Р2

Ответ: число звеньев - 4, из них подвижных - 3; число кинематических пар - 3. Степень подвижности: W = 3* 3 - 2*1- 2 = 5.

Задача 2

Провести графоаналитическим методом силовой анализ

шарнирного четырехзвенника

Известен закон движения качания звена 1, выполнен кинематический анализ и определены силы и пары сил инерции, которые, складываясь с внешними силами, дают для каждого звена результирующую силу P_i (i=1,2,3) и одну пару сил с моментом. M_i (i=1,2,3).

Решение задачи начинают с рассмотрения условия равновесия двухзвенной группы, образованной звеньями 2 и 3. Определяются реакции

P₁₂, P₀₃, P₂₃ = -P₃₂, т. е. 3-х векторов, т. е. 6 скалярных величин.

В данном примере система из 6 уравнений разделена на два скалярных уравнения (каждое имеет по одному неизвестному) и два векторных уравнения, решаемых независимо.

Решение уравнения состоит из трех этапов:

Этап 1. Определение тангенциальных составляющих P₁₂^t и P₀₃^t.

Реакции P₁₂ и P₀₃ раскладываются на две составляющие:

нормальные P₁₂ⁿ и P₀₃ⁿ - направлены по отрезкам BC и CD, а тангенциальные P₁₂^t и P₀₃ ^t -^ им. Направления этих составляющих выбираем произвольно.

Составляются уравнения M_c(P_i)=0 для звеньев 2 и 3:

P₁₂^tl_BC + M₂ - P₂ h₂ M_c = 0,

P₀₃^tl_CD + M₃ - P₃ h₃ M_c = 0,

где плечи h₂ и h₃ измеряется относительно точки С по чертежу (мм). Моменты M₂ и M₃ подставляются со своими знаками.

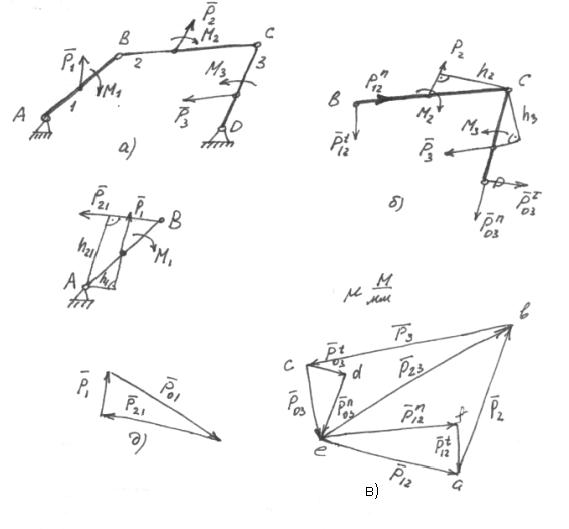
Рис. 4.3 Планы сил механизма

Этап 2. Определение нормальных составляющих P₁₂ⁿ и P₀₃ⁿ выполняют на основании графического решения векторного уравнения S сил, действующих на всю структурную группу в целом:

P₁₂ⁿ + P₁₂^t + P₂ + P₃ + P₀₃^t + P₀₃ⁿ = 0.

//ВС ^CD

В результате построения образуется замкнутый векторный контур – план сил.

Выбрав масштабный коэффициент m_p в Н/мм, откладываем на плане сил (рис. 6.3.в) векторное изображение силы P₂ и P₃ модули которых равны:

(aв) = P₂ /m_p и (вc) = P₃/m_p.

Затем проводим тангенциальную составляющую P₁₂^t по соседству с P₂ и тангенциальную составляющую P₀₃^t по соседству с P₃, причем

(fa) = P₁₂^t/m_p и (cd) = P₀₃^t/m_p.

Стрелки всех векторов должны соответствовать одному и тому же направлению обхода контура.

Направления нормальных составляющих P₁₂ⁿ и P₀₃ⁿ: проводим начала P₁₂^t и конца вектора P₀₃^t. Точка е пересечения этих направлений определит отрезки (de) и (ef), изображающие нормальные составляющие P₁₂ⁿ и P₀₃ⁿ. Сумма нормальных и тангенциальных составляющих дают реакции P₁₂ и P₀₃.

Этап 3: Определение реакций P₂₃ = - P_32.

Это реакция находится из уравнения равновесия сил, действующих на звенья 3 и 2 (на примере звена 3):

P₃ + P₀₃ + P₂₃= 0.

Для его решения достаточно соединить точки (в) и (е) плана сил P₂₃ – направлен к точки (в), а P₃₂ в противоположную сторону к точке (е).

Для начального звена 1 составляется одно векторное уравнение. Суммы сил и одно скалярное уравнение суммы моментов сил относительно точки А:

P₁ + P₂₁ + P₀₁= 0,

P₁ h₁m_е + P₂₁ h₂₁m_е – M₁= 0.

Из первого уравнения плана сил находим реакцию P₀₁, а второе уравнение должно дать тождество, если закон движения начального звена, принятый при определении сил инерции, соответствует внешним силам.

Если момент M₁ является неизвестной: из последнего уравнения находят величину M₁, действующего на начальное звено, которая соответствует принятому движению этого звена.

Момент сил, действующих на вращающееся начальное звено, определяемый из условия заданного закона движения этого звена называется “уравновешивающим моментом”. Аналогично определяется «уравновешивающая сила».

Задача 3

Для заданной схемы нагружения стержня постоянного сечения (рис. 4.4) F=5,0 кН

– построить эпюры внутренних сил;

- построить в общем виде эпюры напряжений;

- определить опасный участок;

- из условия прочности (s_max = [s]) = 120 МПа определить размер сечения;

- определить напряжения на участках стержня и построить эпюры напряжений стержня.

2) определить размеры равнопрочного стержня и экономию материала при равнопрочном стержне.

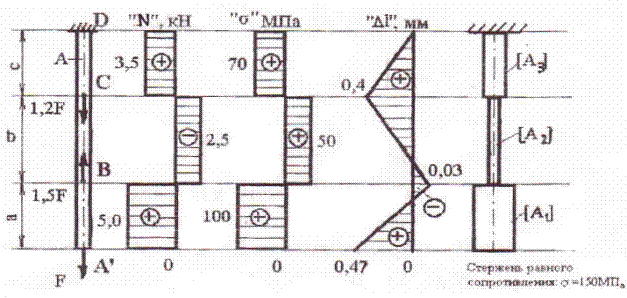
Рис.4.4

Решение:

1. Разбиваем стержень на три участка: A׳B, BC, CD.

2. Определяем внутренние силы на каждом участке стержня.

N₁ = N_(AB) =F = 5,0 kH

N₂ = N_(BC) = F-1,5F = -2,5 kH

N₃ = N_(CD) = F-1,5F+1,2F = 0,7F = 3,5kH

3. Определяем напряжения на каждом участке.

s₍₁₎ =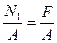

s_(II) =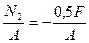

s_(III) =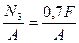

4. Определяем опасный участок.

Опасный участок АВ, где действует сила N₁=N_max=F=5,0 kH

5. Из условия прочности определим площадь сечения.

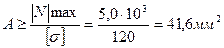
Принимаем А= 50 мм²

6. Определяем численные значения напряжений

s₍₁₎=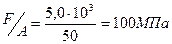

s₍₂₎=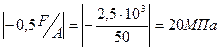

s₍₃₎=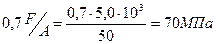

По полученным данным строим эпюру напряжений

7. Определяем перемещения на участках стержня

Е- модуль продольной упругости, Е= 2×10⁵ МПа (для стали)

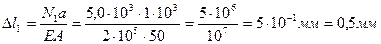
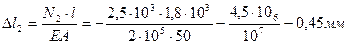
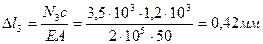
По полученным данным строим эпюру перемещений.

8. По полученным данным определяем размеры сечений равнопрочного стержня, у которого напряжения на каждом участке s_i=[s], i = 1,2,3.

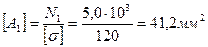
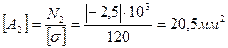
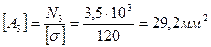
9. Определяем экономию материала в равнопрочном стержне.

Вес стержня с постоянным сечением, g - удельный вес.

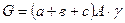
Вес равнопрочного стержня.

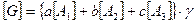
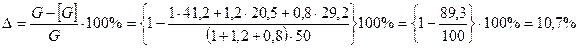
Задача 4

При заданной схеме нагружения стальной балки двутаврового сечения (рис. 4.5):

-построить эпюры Q(x) и M(x)

-определить величины заданных внешних нагрузок q, F и M.

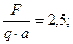
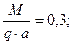
Дано: 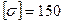МПа; 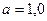м; двутавр №18

Решение:

1. Определяем опорные реакции

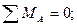
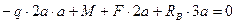
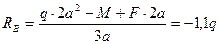
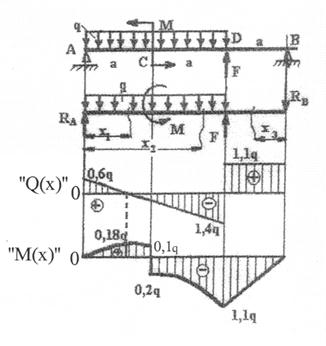
Рис. 4.5

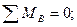
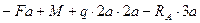
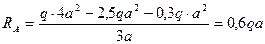
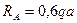= 0,6а

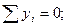
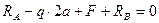
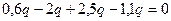
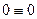
2. Разбиваем балку О на 3 участка (АС; СD; DB)

Участок АС(0 £ x ₁ £ a)

Q _(x1) = R_A - q× x₁; M (x ₁) = R_A × x ₁ – q× x ₁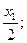

x₁=0; Q (0) = R_A = 0,6 q x₁=0; M (0) = 0

x₁=a; Q (a) = R_A – qa = 0,6 q-q =-0,4 q x₁=a; M (a) = 0,6 q × 1- q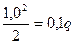

Находим М_max. R_A - q 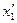=0;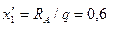

M(x₁)_max=0,6q× 0,6 -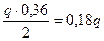

Участок CD (a £ x ₂ £ 2 a)

=

=

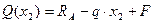
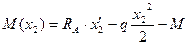
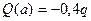
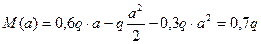
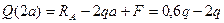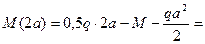
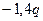
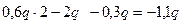
Участок DB (0 £ x ₃ £ a)

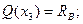
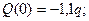
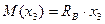
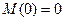
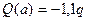
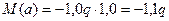
По полученным результатам строим эпюры Q и M. В точке d эпюры изгибающих моментов.

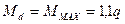, - это опасное сечение (при а=1м).

По заданной величине допустимого напряжения [s] = 150 МПа определяем величины предельных нагрузок.

Для двутавра №18 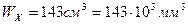(по таблицам сортамента)

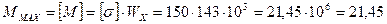kH×м

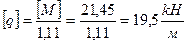
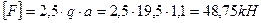
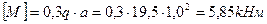
Задача 5

Определить длину 1 сварного соединения в нахлестку двух стальных листов толщиной δ= 5,0 мм, шириной а = 100 мм, нагруженного растягиваю-щими силами F = 25 кН.

Дата добавления: 2014-12-08