Уравнение Эйлера. Теоретический и действительные напоры, развиваемые рабочим колесом

Напор, развиваемый рабочим колесом центробежной машины, зависит от скорости потока, проходящего через рабочее колесо, и от его размеров. Основная задача теории центробежных машин состоит в установлении этой зависимости.

Кинетическая структура потока во вращающихся криволинейных каналах сложная и требует некоторого упрощения.

Полученный таким путём результат может быть скорректирован введением опытных коэффициентов.

Введём следующие предположения: 1) поток имеет струйчатую структуру, т.е. состоит из множества струй, повторяющих геометрическую форму лопасти; 2) имеет место осевая симметрия потока, т.е все струи, составляющие поток, одинаковы геометрически и кинематически; 3) поток является плоским, т.е. градиент скорости вдоль оси, параллельной геометрической оси машины отсутствует.

Первые два предположения можно полагать осуществимыми только при бесконечно большом количестве рабочих лопастей при условии, что лопасти не имеют толщины и, следовательно, не уменьшают проходное сечение межлопастных каналов. Поэтому в последующем изложении параметры машины, вычисляемые при указанных предположениях, обозначаются индексом 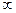и называются параметрами при бесконечном количестве лопастей.

Применим к потоку, проходящему через колесо центробежной машины, уравнение моментов количества движения: импульс момента внешних сил, действующих на массу, состоящую из любых материальных частиц, равен изменению момента количества движения этой массы.

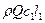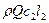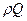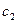Пусть через колесо машины проходит расход Q жидкости или газа с постоянной плотностью , моменты количества движения, отнесенные к 1 с, составят на входе и на выходе из колеса. Здесь - массовый расход через колесо; и - абсолютные средние скорости потока на входе и выходе межлопастных каналов; 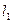и 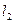- плечи скоростей и 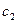(рис.2.2).

Если обозначить 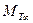теоретический момент, передаваемый потоку с вала (в предположении бесконечного количества лопастей и при отсутствии потерь в процессе преобразования механической энергии в гидравлическую), уравнение моментов количества движения для времени 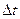, с будет иметь вид

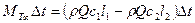. (2.2)

Момент, подводимый от двигателя к валу машины больше 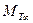вследствие механического трения в подшипниках и уплотнения вала, наличия объёмных потерь и трения нерабочих поверхностей колёс о жидкость (газ).

Введём в уравнение (2.2) конструктивные радиусы 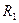и 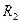: 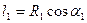, тогда

(2.3)

Здесь 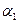и 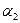- углы между абсолютными и переносными скоростями на входе и выходе.

На рис. 2.2 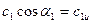; 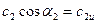, следовательно

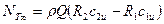. (2.4)

Мощность, передаваемая потоку в межлопастных каналах

,

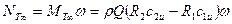или

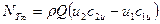. (2.5)

Теоретическая мощность при бесконечном количестве лопастей может быть вычислена как произведение массы, проходящей через рабочее колесо в секунду, на соответствующую удельную работу:

(2.6)

Из сопоставлении (2.5) и (2.6) следует

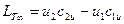(2.7)

Связь удельной работы и напора можно выразить с помощью равенства

.

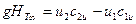Поэтому

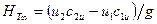(2.8)

Теоретическое давление 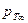получается из (2.8) и из соотношения гидромеханики 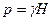, где 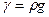- удельный вес среды,

. (2.9)

Уравнения (2.4), (2.5) и (2.8) – основные уравнения центробежной машины. Уравнение (2.8) называется уравнением Эйлера.

При использовании основных уравнений скорост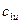и и по окружностям радиусов 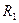и 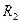принимаются постоянными, так же как и прочие составляющие параллелограммов скоростей на входе и выходе. В действительности это не так, потому что лопасти, развивая силу взаимодействия с потоком, равны по теореме Жуковского о подъёмной силе крыла иметь положительные значения циркуляции, что имеет место только при различных значениях относительной скорости на выпуклой (рабочей) и вогнутой (нерабочей) поверхности лопастей. Таким образом, относительная скорость в межлопастных каналах должна изменяться от наибольшего значения на вогнутой стороне до наименьшего значения на выпуклой, а не оставаться постоянной.

В изложенном заключается парадоксальность рассмотренной струйной теории центробежной машины.

Из параллелограммов на входе и выходе следует

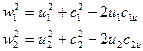
Определив отсюда произведения 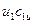и 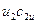и внеся полученные выражения в (2.8), получим уравнение

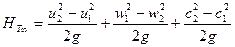. (2.10)

Первый член этого уравнения – напор, обусловленный работой центробежной силы жидкости (газа).

Члены уравнения (2.10) 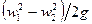и 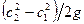выражают прирост напора вследствие преобразования кинетических энергий относительного и абсолютного движения в межлопастных каналах.

Скоростной напор, создаваемый лопастями рабочего колеса, при принятых ранее допущениях равен

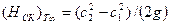, (2.11)

потому что абсолютная скорость потока повышается колесом от до 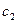. Поэтому теоретический статический напор составит

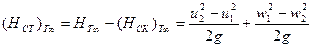(2.12)

Из последнего равенства следует, что повышение статического напора и давления лопастным колесом центробежной машины происходит за счёт работы центробежных сил и снижения кинетической энергии относительного движения.

Если выполнить межлопастные каналы так, что их сечение по всей длине будет постоянно, то 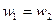и теоретическое статическое давление, развиваемое таким колесом

(2.13)

Тангенциальная составляющая абсолютной скорости 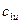характеризует закрученность потока перед входом в межлопастные каналы. Удельная работа, затрачиваемая на закручивание, численно равна 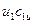, Дж/кг; она передвётся жидкости и суммируется с работой, передаваемой потоку рабочими лопастями. Поэтому в соответствии с (2.7) удельная кинетическая энергия потока на выходе из рабочего колеса

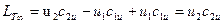(2.14)

Следовательно, при определении теоретических параметров машин, не имеющих на входе специальных устройств, закручивающих поток, основные уравнения представляются в следующем виде

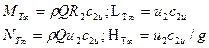(2.15)

Равенства (2.15) обычно называют основными уравнениями центробежной машины с радиальным входом (при 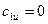абсолютная скорость радиальна).

Из треугольника скоростей на входе при 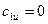следует ; поэтому уравнения (2.10) – (2.12) дают следующие, характерные для машин с радиальным входом значения теоретических напоров:

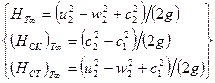(2.16)

Действительный напор, развиваемый колесом, меньше теоретического при бесконечном количестве лопастей, 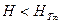. Это объясняется тем, что 1) часть энергии, получаемой потоком в межлопастных каналах, затрачивается на преодоление гидравлического сопротивления проточной полости машины (это обстоятельство учитывают введением в расчёт гидравлического КПД 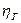, оценивающего совершенство проточной части машины); 2) уравнение Эйлера (2.8) получено в предположении осевой симметрии потока, т.е. при постоянном осреднённом значении на выходе из межлопастных каналов. Однако в действительности скорости распределены по выходному сечению рабочего колеса неравномерно, и поэтому переход от 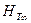к 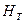можно провести по формуле

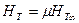, (2.17)

Где <1 – поправочный коэффициент, учитывающий конечное число лопастей.

Кроме этого, действительный напор можно вычислить по формуле

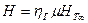(2.18)

Для Современных центробежных машин 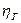=0,80 – 0,96.

Из ряда соотношений для определения поправочного коэффициент часто пользуются формулой чешского профессора Стодолы

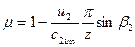
Где 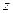- количество лопастей рабочего колеса насоса.

При ориентировочных расчётах .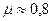

Дата добавления: 2014-12-08