Подобие центробежной машины. Коэффициент быстроходности. Формулы пропорциональности

Движение жидкостей (газов) в проточной части машины очень сложное. Поэтому точный расчёт её рабочих элементов затруднён. При проектировании насосов и компрессоров широко используются опытные данные, полученные при исследовании машин, аналогичных проектируемой. Использование опытных данных при проектировании осуществляется при соблюдении законов подобия.

В современном гидромашиностроении широко применяется метод моделирования, т.е. испытания моделей, позволяющих проверить проект и внести в него практические коррективы. Модели строят, как правило, с соблюдением законов подобия.

Физические явления, протекающие в геометрически подобных пространствах, называют подобными, если в соответствующих точках этих пространств сходные физические величины находятся в постоянных соотношениях. Эти соотношения называются коэффициентами или масштабами подобия.

Пусть машины и подобны (рис.2.33)

Рисунок 2.33 Параллелограммы скоростей подобных центробежных машин

Условия геометрического подобия этих машин заключается в равенстве сходных углов и постоянстве отношений сходных геометрических величин:

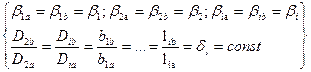(2.76)

где - коэффициент геометрического подобия.

Кинематическое подобие состоит в постоянстве отношений скоростей в сходных точках геометрически подобных машин и равенстве сходных углов параллелограммов скоростей:

(2.77)

где - коэффициент кинематического подобия.

Динамическое подобие выражается постоянством отношений сил одинаковой природы, действующих в сходных точках геометрически и кинематически подобных машин:

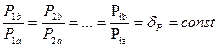(2.78)

где - коэффициент динамического подобия.

Из изложенного следует, что доказательство подобия течений в двух насосах заключается в обнаружении постоянства коэффициентов подобия для сходственных точек.

Если известны коэффициенты подобия двух машин, то по известным характеристикам одной машины можно получить значения сходных характеристик другой машины:

.

Общие критерии подобия потоков, известные в гидромеханике как числа Рейнольдса: 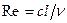; Фруда: ; Эйлера: ; Струхала: , применимы и к потокам центробежных машин.

Подобие течений характеризуется следующими равенствами безразмерных критериев, вычисленных для сходных точек машин:

. (2.79)

Для компрессоров число Эйлера выражают через местную скорость звука и показатель адиабаты между которыми существует зависимость . Следовательно, и поэтому

.

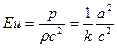Безразмерную скорость обозначают через . Тогда поэтому для подобных компрессоров .

Следовательно, условия подобия компрессоров выражаются следующими равенствами:

(2.80)

В процессе работы компрессора проявляется теплоотдача и для строгого соблюдения подобия следует сохранять ещё и постоянство критериев Прандля и Грасгофа.

Заводы, изготовляющие центробежные машины, обычно имеют в производстве не случайные типы машин, различающиеся размерами и геометрической формой, а серии геометрически подобных машин. Поэтому важно установить соотношения между параметрами машин данной серии.

Пусть две подобные машины и с радиальным входом работают в подобных режимах (рис.2.33). При этом должны соблюдаться условия кинематического подобия.

Объёмная подача для обеих машин

Рассмотрим соотношение этих подач:

.

Из подобия планов скоростей на выходе и условия пропорциональности окружной скорости частоте вращения рабочего колеса машины следует

.

Поэтому

.

Вследствие геометрического подобия машин

,

следовательно, в окончательном виде

(2.81)

Объёмные подачи центробежных машин, работающих в подобных режимах, относятся как кубы наружных диаметров рабочих колёс и первые степени частот вращения валов и объёмных КПД.

Если рассматривать центробежную машину данного размера, то и, следовательно,

(2.82)

При изменении частоты вращения вала центробежной машины объёмные подачи её в подобных режимах относятся как первые степени частот вращения вала и объёмных КПД.

Полные напоры центробежных машин в подобных режимах можно выразить формулой (без вывода)

. (2.83)

Полные напоры, создаваемые центробежными машинами в подобных режимах, относятся как квадраты наружных диаметров рабочих колёс, квадраты частот вращения вала и первые степени гидравлических КПД.

Для данной машины при переменной частоте вращения

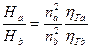(2.84)

При изменении частоты вращения вала центробежной машины напоры, создаваемые ею в подобных режимах, относятся как квадраты частот вращения вала и первые степени гидравлических КПД.

Соотношение между давлениями, создаваемыми машинами, получается умножением обеих частей уравнения (2.83) на соответствующие значения плотностей:

(2.85)

Для данной машины при разных частотах вращения её вала

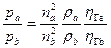(2.86)

Давления, создаваемые центробежной машиной в подобных режимах, пропорциональны плотности перемещаемой ею среды (жидкости или газа).

Мощности центробежных машин, работающих в подобных режимах можно выразить формулой (без вывода)

(2.87)

Мощности центробежных машин, работающих в подобных режимах, относятся как пятые степени наружных диаметров рабочих колёс, кубы частот вращения валов, первые степени плотностей перемещаемых машинами сред и обратно пропорциональны КПД.

Для машины, подающей несжимаемую жидкость, ; и формула (2.87) приобретает вид

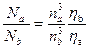(2.88)

Соотношения (2.82), (2.84), (2.88) называются формулами пропорциональности. Для удобства пользования изложенным материалом ниже приведены формулы пропорциональности при изменении параметров :

Применяя формулу пропорциональности,. Можно принимать КПД машин, работающих в подобных режимах, практически одинаковыми.

При строгих расчётах следует иметь в виду некоторое повышение КПД при увеличении размеров машины.

Важной величиной, определяющей подобие течений в насосах, является коэффициент быстроходности .

Коэффициент быстроходности данной машины называют число, равное частоте вращения машины, геометрически подобной данной. Но имеющей подачу и напор =0,102 м (соответственно =1 Дж/кг) в режиме максимального КПД.

Исходя из этого получаем

; (2.89)

(2.90)

Решение этих уравнений даёт

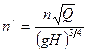. (2.91)

Коэффициент быстроходности - безразмерная величина, являющаяся коэффициентом подобия. В практике насосостроения в качестве коэффициента быстроходности применяют размерную величину

, (2.92)

отнесённую к единичным величинам ; Формула (2.92) получается из условий подобия (2.81), (2.83), (2.87).

Коэффициент быстроходности 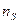определяется подачей, напором, и частотой вращения; при регулировании машины он может изменяться в пределах от 0 до .

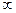Характеризуя машину при помощи 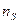, обычно относят его к режиму с максимальным КПД.

Значения 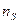для различных типов насосов следующие:

Ротационные и поршневые………………………………………… 40

Вихревые…………………………………………………………….10 – 40

Центробежные………………………………………………………40 – 300

Диагональные……………………………………………………….300 – 600

Осевые……………………………………………………………….600 – 1200

При помощи коэффициента быстроходности, вычисленного по выражению (2.92) можно выбирать тип машины для работы с заданными напором. Подачей, частотой вращения.

Дата добавления: 2014-12-08