Влияние частоты вращения на характеристики насоса

Перерасчёт характеристик при изменении частоты вращения машины и вязкости среды

Пусть задана характеристика 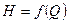насоса (вентилятора) при частоте вращения 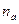(рис. 2.34).

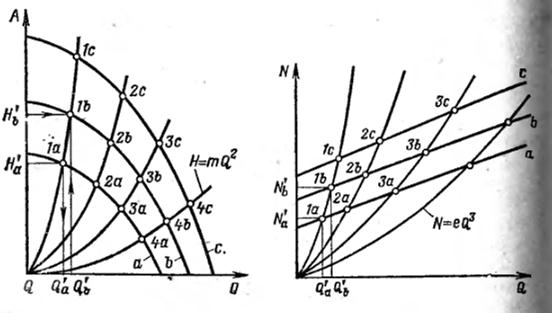
Рисунок 2.34 Построение Рисунок 2.35 Построение характеристик

характеристик 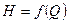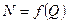по формулам

по формулам пропорциональности

пропорциональности

Требуется перестроить эту характеристику на другую частоту вращения 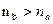, полагая гидравлический и объёмный КПД не зависящими от частоты вращения.

Из формул пропорциональности следует

; .

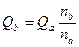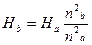Выбрав на характеристике а произвольную точку 1а, находим на координатных осях численные значения 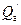и 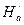. Затем вычисляем координаты точки 1b (характеристики для частоты вращения 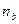) 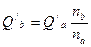и 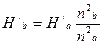и по этим координатам наносим на графике точку 1b.

Аналогично по координатам произвольно выбранных точек 2а. 3а, 4а … вычисляем координаты точек 2b,3b,4b … и соединяем их плавной линией, получаем характеристику 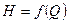для частоты вращения вала 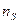. Также можно построить 1с,2с,3с… характеристики при других частотах. Соединив точки 1а,1b,1с…,2а,2b,2с…, 3а,3b,3с…, получим параболические кривые, удовлетворяющие уравнению 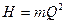, называемые линиями пропорциональности (т – коэффициент пропорциональности уравнения квадратичной параболы).

При расчёте координат КПД машины принимается постоянным, не зависящим от частоты вращения. Поэтому линии пропорциональности являются линиями постоянных КПД машины.

Точки пересечения линий пропорциональности и характеристик 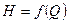при разных частотах вращения определяют параметры Q и Н машины в подобных режимах работы.

Пересчёт характеристик 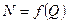проводится аналогичным способом по формулам пропорциональности

; .

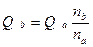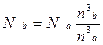Пересчёт характеристик 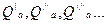и 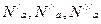… произвольно взятых точек 1а,2а,3а … получим пересчётом координатных точек 1b,2b,3b … и 1с,2с,3с …, по которым проводим кривые зависимости мощности от подачи при частотах вращения 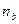и 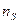(линии b и с на рис. 2.35).

Линии 1а,1b,1с…,2а,2b,2с… являются линиями подобных режимов с постоянным для каждой из них значением КПД. Общий вид уравнений этих линий

,

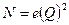где е – коэффициент пропорциональности уравнений кубической параболы.

В общем случае работы машины на сеть, напор, который подчинён уравнению 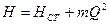, КПД машины при изменении режима изменяется. Условие 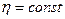при изменении частоты вращения соблюдается только в том случае. Когда напор в сети подчинён законам квадратичной параболы 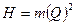, т.е. в сети нет статического напора.

Выясним, как изменяется форма характеристики КПД 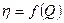при изменении частоты вращения (рис.2.36). Даны характеристик напора и КПД при частоте вращения 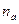(кривые показаны сплошными линиями). Проведём линии подобных режимов 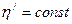; 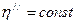(режимы I и II).

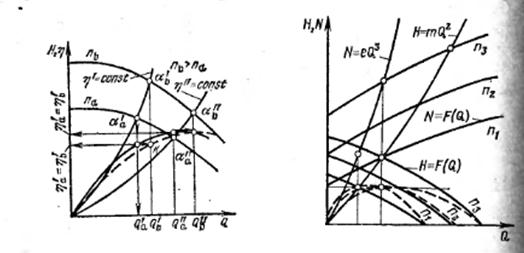
Рисунок 2.36 Влияние частоты Рисунок 2.37 Характеристики

вращения на характеристику центробежной машины при

КПД переменной частоте вращения

При частоте вращения 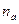и режиме работы I параметры машины 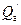и 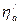определяет точка 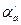. Если частота вращения изменится до 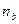, то подача 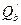определится точкой 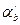, а КПД останется прежним, т.е. .

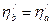Следовательно, соответственная точка к кривой КПД при частоте вращения 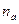получается перенесением по горизонтали значения 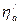на ординату, соответствующую абсциссе 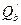. Аналогичное построение дано на графике для режима II.

Таким образом, при увеличении частоты вращения характеристики КПД деформируются в направлении, параллельном оси абсцисс.

На рис. 2.37 представлена совместная характеристика напора, мощности и КПД центробежной машины для трёх различных частот вращения. Такое семейство кривых, связанное условиями подобия, называется характеристикой при переменной частоте вращения.

Дата добавления: 2014-12-08