
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач. Пример 1. На тонком стержне длиной l = 20 см находится равномерно распределенный электрический заряд
|
|
|
|
Пример 1. На тонком стержне длиной l = 20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд q1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность τ заряда на стержне.
Р е ш е н и е. Сила взаимодействия F заряженного стержня с точечным зарядом q1 зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ. При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (рис. 1) малый участок dr с зарядом dq = τdr. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона,

Интегрируя это выражение в пределах от 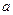 до
до 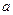 +
+ 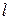 , получаем
, получаем
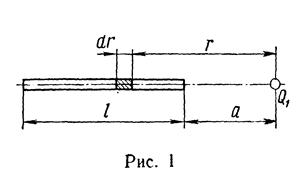
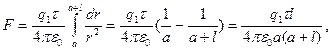 откуда
откуда
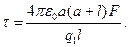
Проверим, дает ли расчетная формула единицу линейной плотности электрического заряда. Для этого в правую часть формулы вместо символов величин подставим их единицы:
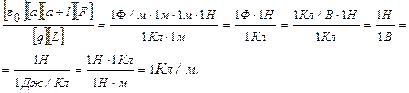
Найденная единица является единицей линейной плотности заряда.
Произведем вычисления:

Пример 2. По тонкому кольцу равномерно распределен заряд q = 40 нКл с линейной плотностью τ = 50 нКл/м. Определить напряженность 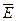 электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстоянии, равное половине радиуса.
электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстоянии, равное половине радиуса.
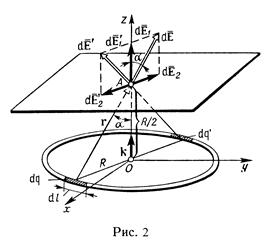
Р е ш е н и е. Совместим координатную плоскость xOy с плоскостью кольца, а ось Oz – с осью кольца (рис. 2). На кольце выделим малый участок длиной dl. Так как заряд dq=τdl, находящийся на этом участке, можно считать точечным, то напряженность d 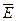 электрического поля, создаваемого этим зарядом, может быть записана в виде
электрического поля, создаваемого этим зарядом, может быть записана в виде
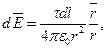
где 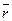 – радиус-вектор, направленный от элемента dl к точке А.
– радиус-вектор, направленный от элемента dl к точке А.
Разложим вектор d 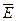 на две составляющие: d
на две составляющие: d 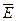 1, перпендикулярную плоскости кольца (сонаправленную с осью Oz), и d
1, перпендикулярную плоскости кольца (сонаправленную с осью Oz), и d 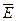 2, параллельную плоскости кольца (плоскости xOy), т. е.
2, параллельную плоскости кольца (плоскости xOy), т. е.
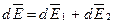 .
.
Напряженность 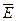 электрического поля в точке А найдем интегрированием:
электрического поля в точке А найдем интегрированием:
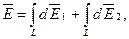
где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов dq и dq` (dq = dq`), расположенных симметрично относительно центра кольца, векторы d 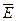 2 и d
2 и d 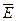 2` в точке А равны по модулю и противоположны по направлению: d
2` в точке А равны по модулю и противоположны по направлению: d 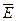 2 = - d
2 = - d 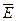 2`. Поэтому векторная сумма (интеграл)
2`. Поэтому векторная сумма (интеграл) 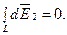 Составляющие d
Составляющие d 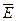 1 для всех элементов кольца сонаправлены с осью Oz (единичным вектором
1 для всех элементов кольца сонаправлены с осью Oz (единичным вектором 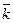 ), т. е. d
), т. е. d 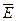 1 =
1 = 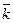 dE1. Тогда
dE1. Тогда
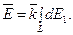
Так как 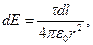
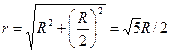 и
и 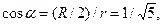 то
то
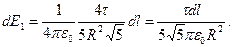
Таким образом,
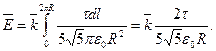
Из соотношения q = 2πRτ определим радиус кольца R = q/(2πτ). Тогда
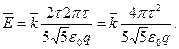
Модуль напряженности
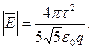 (1)
(1)
Проверим, дает ли правая часть полученного равенства единицу напряженности (В / м):
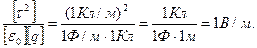
Выразим физические величины, входящие в формулу (1), в единицах СИ (τ = 5·10-8 Кл/м, q=4·10-8 Кл, ε0 = 8,85·10-12 Ф/м) и произведем вычисления:
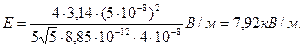
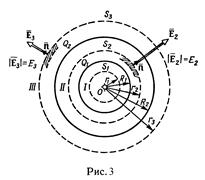 Пример 3. Две концентрические проводящие сферы радиусами R1 = 6 см и R2 = 10 см несут соответственно заряды q1 = 1нКл и q2 = - 0,5нКл. Найти напряженность Е поля в точках отстоящих от центра сфер на расстояниях r1 = 5 см, r2 = 9 см, r3 = 15 см. Построить график E(r).
Пример 3. Две концентрические проводящие сферы радиусами R1 = 6 см и R2 = 10 см несут соответственно заряды q1 = 1нКл и q2 = - 0,5нКл. Найти напряженность Е поля в точках отстоящих от центра сфер на расстояниях r1 = 5 см, r2 = 9 см, r3 = 15 см. Построить график E(r).
1. Для определения напряженности Е1 в области I проведем гауссову поверхность S1 радиусом r1 и воспользуемся теоремой Остроградского – Гаусса:
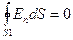
(так как суммарный заряд, находящийся внутри гауссовой поверхности, равен нулю). Из соображений симметрии En=E1=const. Следовательно, 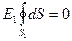 и Е1 (напряженность поля в области I) во всех точках, удовлетворяющих условию r1<R1, будет равна нулю.
и Е1 (напряженность поля в области I) во всех точках, удовлетворяющих условию r1<R1, будет равна нулю.
2. В области II гауссову поверхность проведем радиусом r2. В этом случае (диэлектрическую проницаемость среды будем считать равной единице (вакуум))
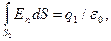
(так как внутри гауссовой поверхности находится только заряд q1).
Так как En = E = const, то Е можно вынести за знак интеграла:
 или ES2 = q1/
или ES2 = q1/ 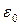 .
.
Обозначив напряженность Е для области II через Е2, получим
Е2 = q1/(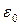 S2),
S2),
где S2 = 4πr22 – площадь гауссовой поверхности. Тогда
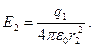 (1)
(1)
3. В области III гауссова поверхность проводится радиусом r3. Обозначим напряженность Е области III через Е3 и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен q1 + q2. Тогда
Е3 = (q1+q2)/4π 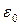 r32.
r32.
Заметив, что q2<0, это выражение можно переписать в виде
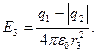 (2)
(2)
Убедимся в том, что правая часть равенства (1) и (2)дает единицу напряженности:

Выразим все величины в единицах СИ (q1 = 10-9 Кл, q2= - 0,5·10-9 Кл, r1=0,09 м, r2=0,15 м, 1/(4πε0)=9·109 м/Ф) и произведем вычисления:

Построим график E(r). В области I(r1<R1) Е = 0. В области II (R1 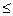 r<R2) E2(r) изменяется по закону 1/r2. В точке r = R1 напряженность E2(R1) = q1/(4π
r<R2) E2(r) изменяется по закону 1/r2. В точке r = R1 напряженность E2(R1) = q1/(4π 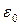 R12)=2,25 кв/м. В точке r = R2 (r стремится к R2 слева) E2(R2) = q1/(4π
R12)=2,25 кв/м. В точке r = R2 (r стремится к R2 слева) E2(R2) = q1/(4π 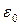 R22) = 0,9 кВ/м. В области III (r>R2) E3(r) изменяется по закону 1/r2, причем в точке r = R2 (r стремится к R2 справа) E3(R2) = (q1 - |q2|/(4π
R22) = 0,9 кВ/м. В области III (r>R2) E3(r) изменяется по закону 1/r2, причем в точке r = R2 (r стремится к R2 справа) E3(R2) = (q1 - |q2|/(4π 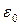 R22) = 0,45 кВ/м. Таким образом, функция E(r) в точках r = R1 и r = R2 терпит разрыв.
R22) = 0,45 кВ/м. Таким образом, функция E(r) в точках r = R1 и r = R2 терпит разрыв.
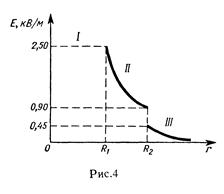
График зависимости E(r) представлен на рис. 4.
Пример 4. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии 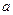 1 = 0,5 см и
1 = 0,5 см и 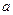 2 = 2 см от поверхности цилиндра, в средней его части.
2 = 2 см от поверхности цилиндра, в средней его части.
Р е ш е н и е. Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала: 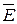 = -grad φ. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде
= -grad φ. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде
E = - dφ/dr, или dφ = - Edr.
Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r1 и r2 от оси цилиндра:
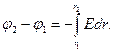
(1)
Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром:
E = τ/(2π 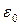 r).
r).
Подставив выражение Е в (1), получим
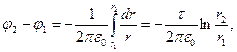
или
φ1 – φ2 = τ/(2π 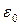 )ln(r2/r1). (2)
)ln(r2/r1). (2)
Произведем подстановку, учитывая, что величины r1 и r2, входящие в формулу (2) в виде отношения, можно выразить в сантиметрах (r1 = R + 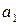 = 1,5 см r2 = R +
= 1,5 см r2 = R + 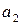 = 3 см):
= 3 см):
φ1 – φ2 = 2 · 10 –8 · 1,8 · 1010 ln(3/1,5) = 3,6 · 102 · 2,3 ln2 В = 250 В.
Пример 5. Конденсатор емкостью С1 = 3 мкФ был заряжен до разности потенциалов U1 = 40 В. После отключения от источника тока конденсатор соединили с другим незаряженным конденсатором емкостью С2 = 5 мкФ. Какая энергия 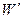 израсходуется на образование искры в момент присоединения второго конденсатора?
израсходуется на образование искры в момент присоединения второго конденсатора?
Р е ш е н и е. Энергия, израсходованная на образование искры,
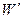 = W1 – W2, (1)
= W1 – W2, (1)
где W1 – энергия, которой обладает первый конденсатор до присоединения к нему второго конденсатора; W2 – энергия, которую имеет батарея, составленная из двух конденсаторов.
Энергия заряженного конденсатора определяется по формуле
W = ½СU2, (2)
где С – емкость конденсатора или батареи конденсаторов.
Выразив в формуле (1) энергии W1 и W2 по формуле (2) и приняв во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим
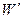 = ½ C1U12 – ½(C1 + C2)U22, (3)
= ½ C1U12 – ½(C1 + C2)U22, (3)
где U2 – разность потенциалов на зажимах батареи конденсаторов.
Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U2 следующим образом:
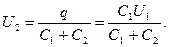
Подставив выражение U2 в (3), найдем
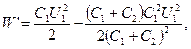
или
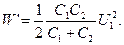
Произведем вычисления:
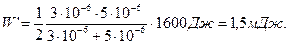
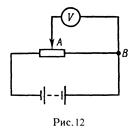 Пример 6 Потенциометр сопротивлением R = 100 Ом подключен к батарее с ЭДС e = 150 В и внутренним сопротивлением Ri = 50 Ом. Определить: 1) показание вольтметра между сопротивлением Rv = 500 Ом, соединенного с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра; 2) разность потенциалов между теми же точками потенциометра при отключении вольтметра.
Пример 6 Потенциометр сопротивлением R = 100 Ом подключен к батарее с ЭДС e = 150 В и внутренним сопротивлением Ri = 50 Ом. Определить: 1) показание вольтметра между сопротивлением Rv = 500 Ом, соединенного с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра; 2) разность потенциалов между теми же точками потенциометра при отключении вольтметра.
Р е ш е н и е. 1. Показание вольтметра, подключенного к точкам А и В (рис. 12), определим по формуле
U1 = I1R1,
где R1 – сопротивление параллельно соединенных вольтметра и половины потенциометра; I1 – суммарная сила тока в ветвях этого соединения (она равна силе тока в неразветвленной части цепи).
Силу тока I1 найдем по закону Ома для полной цепи:
I1 = e /(Re +Ri), (1)
где Re – сопротивление внешней цепи. Это сопротивление есть сумма двух сопротивлений:
Re = R/2 +R1. (2)
Сопротивление R1 найдем по формуле параллельного соединения проводников 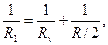 откуда
откуда
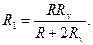
Подставив в (1) выражение Re по (2), найдем
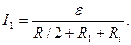
В данном случае решение задачи в общем виде было бы громоздким. Поэтому удобно вычисление величин провести раздельно:
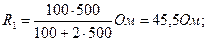

U1 = 1,03·45·5 В = 46,9 В.
2. Разность потенциалов между точками А и В при отключенном вольтметре равна произведению силы тока I 2 на половину сопротивления потенциометра:
U2 = I2 ·R/ 2, (3)
где I2 – сила тока в цепи при отключенном вольтметре. Ее определим по формуле
I2 = e /(R + Ri).
Подставив выражение I2 в (3), найдем
U2 = e / (R + Ri)·R/2.
Произведем вычисления:
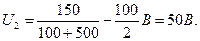
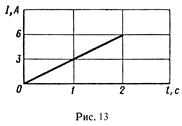 Пример 7 Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δt = 2 с по линейному закону от I0 = 0 до I = 6 А (рис 13). Определить теплоту Q 1, выделившуюся в этом проводнике за первую секунду, и Q2 – за вторую, а также найти отношение q1/q2.
Пример 7 Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δt = 2 с по линейному закону от I0 = 0 до I = 6 А (рис 13). Определить теплоту Q 1, выделившуюся в этом проводнике за первую секунду, и Q2 – за вторую, а также найти отношение q1/q2.
Р е ш е н и е. Закон Джоуля – Ленца в виде Q = I2Rt справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого интервала времени и записывается в виде
dQ = I2Rdt. (1)
Здесь сила тока I является некоторой функцией времени. В данном случае
I = kt, (2)
где k – коэффициент пропорциональности, характеризующий скорость изменения силы тока:
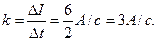
С учетом (2) формула (1) примет вид
dQ = k2Rt2dt. (3)
Для определения теплоты, выделившейся за конечный интервал времени Δ t, выражение (3) надо проинтегрировать в пределах от t 1 до t 2:
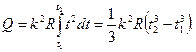
Произведем вычисления:
Q1 = 1/3 · 32 · 20(1 – 0) Дж = 60 Дж;
Q2 = 1/3 · 32 · 20(8 – 1) Дж = 420 Дж.
Следовательно,
Q2 / Q1 = 420 / 60 = 7,
т. е. за вторую секунду выделится теплоты в семь раз больше, чем за первую.
Пример 8 Пространство между пластинами плоского конденсатора имеет объем V = 375 см3 и заполнено водородом, который частично ионизирован. Площадь пластин конденсатора S = 250 см2. При каком напряжении U между пластинами конденсатора сила тока I, протекающего через конденсатор, достигнет значения 2мкА, если концентрация n ионов обоих знаков в газе равна 5,3 · 107 см–3. Принять подвижность ионов b += 5,4 · 10 –4 м2 / (В · с), b -=7,4 · 10-4 м2/(В · с).
Р е ш е н и е. Напряжение U на пластинах конденсатора связано с напряженностью Е электрического поля между пластинами и расстоянием d между ними соотношением
U = Ed. (1)
Напряженность поля может быть найдена из выражения плотности тока
j = qn(b+ + b-)E,
где q – заряд иона.
Отсюда
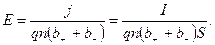
Расстояние d между пластинами, входящее в формулу (1), найдем из соотношения
d = V/S.
Подставив выражения Е и d в (1), получим
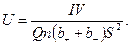
(2)
Проверим, дает ли правая часть полученной расчетной формулы единицу напряжения:
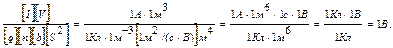
Подставим в формулу (2) значения величин и произведем вычисления:
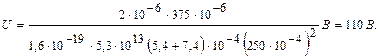
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 1317; Нарушение авторских прав?; Мы поможем в написании вашей работы!