Примеры решения задач 2 страница

откуда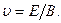

Подставив это выражение ско­рости в формулу (1), получим

.

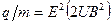Убедимся в том, что правая часть равенства дает единицу удель­ного заряда (Кл/кг):

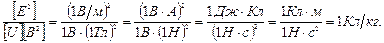
Произведем вычисления:

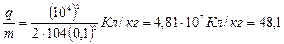МКл/кг.

Пример 8. Плоский квадратный контур со стороной а = 10 см, по кото­рому течет ток I = 100 А, свободно установился в однородном магнит­ном поле (В = 1 Тл). Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) 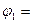90°; 2) 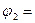3°. При повороте контура сила тока в нем поддерживается неиз­менной.

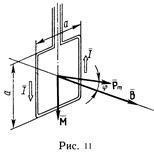Решение. Как известно, на контур с то­ком в магнитном поле действует момент силы (рис. 1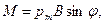1)

(1)

где 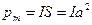– магнитный момент контура; В – магнитная индукция; φ – угол между векторами 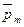(направлен по нормали к контуру) и .

По условию задачи в начальном положении контур свободно ус­тановился в магнитное поле. При этом момент силы равен нулю (М = 0), а значит, φ = 0, т. е. векторы 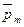и сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменной (зависит от угла поворота 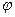), то для подсчета работы применим формулу работы в дифференциальной форме 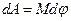. Учитывая формулу (1), получаем

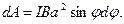
Взяв интеграл от этого выражения, найдем работу при повороте на ко­нечный угол:

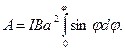(2)

Работа при повороте на угол 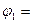90°:

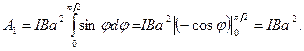(3)

Выразим числовые значения величин в единицах СИ (I =100 А, В = 1Тл, 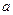= 10 см = 0,1м) и подставим в (3):

.

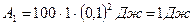Работа при повороте на угол 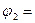3°. В этом случае, учитывая, что угол 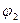мал, заменим в выражении (2) sin φ 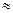φ:

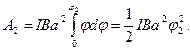(4)

Выразим угол 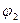в радианах. После подстановки числовых значе­ний величин в (4) найдем

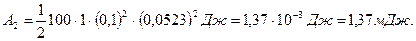
Задачу можно решить и другими способами:

1. Работа внешних сил по перемещению контура с током в маг­нитном поле равна произведению силы тока в контуре на изменение магнитного потока, пронизывающего контур:

,

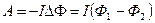где Ф₁ – магнитный поток, пронизывающий контур до перемещения; Ф₂ – то же, после перемещения.

Если 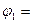90°, то Ф₁ =BS, Ф₂ =0. Следовательно,

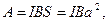
что совпадает с (3).

2. Воспользуемся выражением для механической потенциальной энергии контура с током в магнитном поле

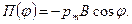
Тогда работа внешних сил

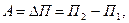
или

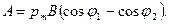
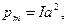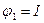Так как cos и cos 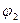= 0, то

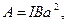
что также совпадает с (3).

Пример 9. В однородном магнитном поле с индукцией В = 0,2Тл рав­номерно вращается катушка, содержащая N = 600 витков, с частотой ν = 6c^-1. Площадь S поперечного сечения катушки 100 см². Ось враще­ния перпендикулярна оси катушки и направлению магнитного поля. Определить максимальную Э.Д.С индукции вращающейся катушки.

Ρ е ш е н и е. Согласно закону Фарадея,

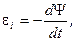
где потокосцепление катушки Ψ = ΝΦ (Ν – число витков, пронизы­ваемых магнитным потоком Ф). При произвольном расположении ка­тушки относительно магнитного поля

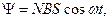(1)

где круговая частота 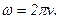Подставив ω в (I), получим

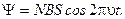
Тогда

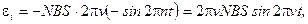
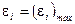при 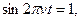поэтому

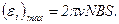
Вычисляя, получаем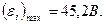

Таблица вариантов для заданий

Вариант	Номера задач

1. Точечные заряды q₁=20 мкКл, q₂=-10 мкКл находятся на рас­стоянии d =5см друг от друга. Определить напряженность поля в точке, удаленной на r₁=3 см от первого и на r₂=4 см от второго за­ряда. Опре­делить также силу 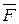, действующую в этой точке на точечный заряд q= 1 мкКл.

2. Три одинаковых точечных заряда q₁=q₂=q₃=2 нКл находятся в вершинах равностороннего тре­угольника со сторонами а =10см. Опре­делить модуль и направление силы 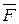, действующей на один из заря­дов со стороны двух других.

3. Два положительных точечных заряда q и 9q закреплены на рас­стоянии d=100см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устой­чивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закреп­ленные заряды.

4. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол a. Ша­рики погружают в масло. Како­ва плотность r масла, если угол расхож­дения нитей при погружении в масло остается неизменным? Плотность материала шариков r₀=1,5×10³ кг/м³, диэлектрическая проницаемость масла e = 2,2.

5. Четыре одинаковых заряда q₁= q₂=q₃=q₄=40кНл закреплены в вершинах квадрата со стороной а =10см. Найти силу 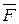, действую­щую на один из этих зарядов со стороны трех остальных.

6. Точечные заряды q₁=30 мкКл и q₂=-20 мкКл находятся на рас­стоянии d =20 см друг от друга. Опре­делить напряженность электриче­ского поля 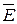в точке, удаленной от первого заряда на расстояние r₁ = 30 см, а от второго – на r₂ = 15 см.

7. В вершинах правильного треугольника со стороной а= 10 см находятся заряды q₁=10мкКл, q₂=20 мкКл и qз=30 мкКл. Определить силу 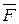, действую­щую на заряд q₁ со стороны двух других зарядов.

8. В вершинах квадрата находятся одинаковые заряды q₁=q₂=q₃=q₄= 8×10^-10 Кл. Какой отрица­тельный заряд q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

9. На расстоянии d=20 см находятся два точечных заряда: q₁=-50 нКл и q₂=100нКл. Определить силу 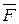, действующую на заряд q₃=-10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.

10. Расстояние d между двумя точечными зарядами q₁=2нКл и q₂=4нКл равно 60см. Определить точку, в которую нужно поместить третий заряд q₃ так, чтобы система зарядов находилась в равновесии. Определить заряд q₃ и его знак. Устойчивое или неустойчивое будет равновесие?

11. Тонкий стержень длиной l =20 см несет равномерно распреде­ленный заряд t=0,1 мкКл. Определить напряженность 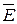электриче­ского поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а=20 см от его конца.

12. По тонкому полукольцу радиуса R=10 см равномерно распре­делен заряд с линейной плотностью t = 1 мкКл/м. Определить напря­женность 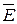электрического поля, создаваемого распределенным заря­дом в точке О, совпадающей с центром кольца.

13. Тонкое кольцо несет распределенный заряд q=0,2 мкКл. Оп­ределить напряженность 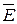электрического поля, создаваемого распределенным зарядом в точке A, равноудаленной от всех точек кольца на расстояние г=20 см. Радиус кольца R=10см.

14. Треть тонкого кольца радиуса R=10см несет распределенный заряд q=50нКл. Определить напряженность 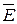электрического поля, создаваемого распре­деленным зарядом в точке О, совпадающей с цен­тром кольца.

15. Бесконечный тонкий стержень, ограниченный с одной сто­роны, несет равномерно распределенный заряд с линейной плотностью t=0,5 мкКл/м. Определить напряженность 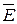электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а =20 см от его начала.

16. По тонкому кольцу радиусом R=20см равномерно распреде­лен с линейной плотностью t=0,2 мкКл/м заряд. Определить напря­женность 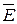электрического поля, создаваемого распределенным заря­дом в точке A, находящейся на оси кольца на расстоянии h=2R от его центра.

17. По тонкому полукольцу равномерно распределен заряд q=20 мкКл с линейной плотностью t=0,1 мкКл/м. Определить напря­женность 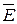электрического поля, создаваемого распределенным заря­дом в точке О, совпадающей с центром кольца.

18. Четверть тонкого кольца радиусом R=10см несет равномерно распределенный заряд q=0,05 мкКл. Определить напряженность 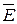электрического поля, создаваемого распределенным зарядом в точке О, совпа­дающей с центром кольца.

19. По тонкому кольцу равномерно распределен заряд q=10 нКл с линейной плотностью t=0,01 мкКл/м. Определить напряженность 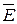электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, рав­ное радиусу кольца.

20. Две трети тонкого кольца радиусом R=10см несут равномерно распределенный с линейной плотностью t=0,2 мкКл/м заряд. Опреде­лить напряженность 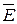электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

21. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями s₁ и s₂ (рис. 5). Требуется: 1) используя теорему Остроградского-Гаусса, найти зави­симость E(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять s₁=4s, s₂=s; 2) вычислить напряжен­ность Е в точке, удаленной от центра на расстояние r, и указать на­правление вектора 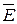.Принять s=30нКл/м², г= l,5R; 3) построить гра­фик E(r).

22. См. условие задачи 21. В п. 1 принять s₁=s, s₂=-s. В п. 2 при­нять s=0,1мкКл/м², r=3.

23. См. условие задачи 21. В п. 1 принять s₁=-4s, s₂=s. В п. 2 принять s=50 нКл/м², r=1,5R.

24. См. условие задачи 21. В п. 1 принять s₁=-2s, s₂=s. В п. 2 принять s=0,1мкКл/м², г==3R.

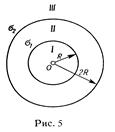
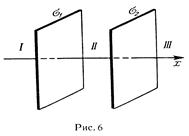
25. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями s₁ и s₂ (рис. 6). Требуется: 1) используя теорему Остроградского-Гаусса и принцип суперпози­ции электрических полей, найти выражение Е(х) напря­жен­ности электрического поля в трех областях: I, II и III.Принять s₁=2s, s₂=s; 2) вычислить напряженность Е по ля в точке, расположенной слева от плоскостей, и указать направление вектора 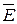; 3) построить график Е(х)

26. См. условие задачи 25. В п. 1 принять s₁=-4s, s₂=2s. В п. 2 принять s=40 нКл/м² и точку расположить между плоскостями.

27. См. условие задачи 25. В п. 1 принять s₁=s, s₂=-2s. В п. 2 принять s=20 нКл/м² и точку располо­жить справа от плоскостей.

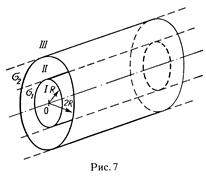
28. На двух коак­сиальных бесконечных цилиндрах радиусами R и 2R равномерно распре­делены заряды с поверх­ностными плот­ностями s₁ и s₂ (рис. 7). Требу­ется:

1) используя теорему Ост­роградского-Гаусса, найти за­висимость Е(r) напряженности электри­ческого поля от расстоя­ния для трех областей: I, II и III. Принять s₁=-2, s₂=s; 2) вычис­лить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направ­ление вектора 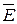. Принять s= 50нКл/м², r = 1,5R; 3) построить график E(r).

29. См. условие задачи 28. В п. 1 принять s₁=s, s₂=-s. В п. 2 при­нять s= 60нКл/м², r =3R.

30. См. условие задачи 28. В п. 1 принять s₁=-s, s₂=4s. В п. 2 принять s= 30нКл/м², r =4R.

31. Два точечных заряда q₁=6нКл и q₂=3нКлнаходятся на рас­стоянии d=60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

32. Электрическое поле создано заряженным проводящим шаром, потенциал j которого 300 В. Определить работу сил поля по переме­щению заряда q= 0,2мкКл из точки 1 в точку 2 (рис.8).

33. Электрическое поле создано зарядами q₁=2мкКл и q₂=-2мкКл, находящимися на расстояние а =10см друг от друга. Определить работу сил поля, совершаемую при перемещении заряда q=0,5мкКл из точки 1 в точку 2 (рис.9).

34. Две параллельные заряженные плоскости, поверхностные плотности заряда которых s₁=2мкКл/м² и s₂=-0,8мкКл/м², находятся на расстоянии d =0,6см друг от друга. Определить разность потенциалов U между плоскостями.

35. Диполь с электрическим моментом р = 100 пКл×м свободно установился в свободном электрическом поле напряженностью Е =200кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол a=180°.

36. Четыре одинаковых капли ртути, заряженных до потенциала j=10В, сливаются в одну. Каков потен­циал j₁ образовавшейся капли?

37. Тонкий стержень согнут в кольцо радиусом R =10 см. Он рав­номерно заряжен с линейной плотностью заряда t=800нКл/м. Опреде­лить потенциал j в точке, расположенной на оси кольца на расстоянии h = 10см от его центра.

38. Поле образовано точечным диполем с электри­ческим момен­том р = 200пКл×м. Определить разность потенциалов U двух точек поля, расположенных симмет­рично относительно диполя на его оси на расстоянии r =40 см от центра диполя.

39. Электрическое поле образовано бесконечно длин­ной заряжен­ной нитью, линейная плотность заряда кото­рой t= 20пКл/м. Опреде­лить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r₁=8см и r₂= 12см.

40. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда t=200пКл/м. Опреде­лить потенциал j поля в точке пересечения диагоналей.

41. Пылинка массой т =200мкг, несущая на себе заряд q=40нКл, влетела в электрическое поле в на­правлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость u = 10 м/с. Определить скорость u₀ пылинки до того, как она влетела в поле.

42. Электрон, обладавший кинетической энергией T = 10 эВ, вле­тел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потен­циалов U= 8В?

43. Найти отношение скоростей ионов Сu⁺⁺ и К⁺, прошедших одинаковую разность потенциалов.

44. Электрон с энергией Т = 400 эВ (в бесконечнос­ти) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Определить минимальное рас­стояние а, на которое приблизится электрон к поверхности сферы, если заряд ее q = - 10 нКл.

45. Электрон, пройдя в плоском конденсаторе путь от одной пла­стины до другой, приобрел скорость u = 10⁵ м/с. Расстояние между пластинами d = 8 мм. Найти: 1) разность потенциалов U между пласти­нами; 2) поверхностную плотность зарядаs на пластинах.

46. Пылинка массой т = 5 нг, несущая на себе N = 10 электронов, прошла в вакууме ускоряющую разность потенциалов U = 1 MB. Ка­кова кинетическая энергия Т пылинки? Какую скорость u приобрела пылинка?

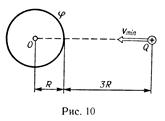
47. Какой минимальной скоростью u_min должен обладать протон, чтобы он мог достигнуть поверхности заряженного до потенциала j = 400 В металлического шара (рис.10)?

48. В однородное электрическое поле напряженностью Е = 200 В/м влетает (вдоль силовой линии) электрон со скоростью u₀=2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.

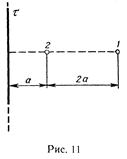
49. Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом (t = 10 нКл/м). Опреде­лить кинетическую энергию Т₂ электрона в точке 2, если в точке1его кинетическая энергия T₁= 200эВ (рис.11).

50. Электрон движется вдоль силовой линии однородного элек­трического поля. В некоторой точке поля с потенциалом j₁ = 100 В электрон имел скорость 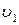= 6 Мм/с. Определить потенциал j₂ точки поля, дойдя до которой электрон потеряет половину своей ско­рости.

51. Конденсаторы емкостью C₁ = 5 мкФ и С₂ = 10 мкФ заряжены до напряжений U₁ = 60 В и U₂ = 100 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обклад­ками, имеющими одноименные заряды.

52. Конденсатор емкостью C₁ = 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденса­тор ем­костью С₂ = 20 мкФ.

53. Конденсаторы емкостями C₁ = 2 мкФ, С₂ = 5 мкФ и С₃ = 10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить на­пряжение и заряд на каждом из конденсато­ров.

54. Два конденсатора емкостями C₁ = 2 мкФ и С₂ = 5 мкФ заря­жены до напряжений U₁ = 100 В и U₂ = 150 В соответственно. Опреде­лить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.

55. Два одинаковых плоских воздушных конденсато­ра емкостью С=100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

56. Два конденсатора емкостями C₁ = 5 мкФ и С₂ = 8 мкФ соеди­нены последовательно и присоединены к батарее с ЭДС e = 80 В. Оп­ределить заряды q₁ и q₂ конденсаторов и разности потенциалов U₁ и U₂. между их обкладками.

57. Плоский конденсатор состоит из двух круглых пластин радиу­сом R = 10см каждая. Расстояние между пластинами d = 2 мм. Конден­сатор присоединен к источ­нику напряжения U = 80 В. Определить заряд q и на­пряженность Е поля конденсатора в двух случаях: а) ди­электрик — воздух; б) диэлектрик — стекло.

58. Два металлических шарика радиусами R₁ = 5 см и R₂ = 10 см имеют заряды q₁ = 40 нКл и q₂ = -20 нКл соответственно. Найти энер­гию W, которая выделится при разряде, если шары соединить проводни­ком.

59. Пространство между пластинами плоского конденсатора за­полнено двумя слоями диэлектрика: стекла толщиной d₁ = 0,2 см и слоем парафина толщиной d₂ = 0,3 см. Разность потенциалов между обкладками U = 300 В. Определить напряженность E поля и падение потенциала в каждом из слоев.

60. Плоский конденсатор с площадью пластин S = 200 см² каждая заряжен до разности потенциалов U =2 кВ. Расстояние между пласти­нами d=2 см. Диэлектрик – стекло. Определить энергию W поля кон­денсатора и плотность энергии w поля.

61. Катушка и амперметр соединены последовательно и подклю­чены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением r = 4 кОм. Амперметр показывает силу тока I = 0,3 А, вольтметр напряжение U = 120 В. Определить сопротивление Rка­тушки. Определить относительную погрешность e, которая будет до­пущена при измерении сопротивления, если пренебречь силой тока, текущего через вольтметр.

Дата добавления: 2014-12-08