Примеры решения задач 1 страница

Пример 1. По отрезку прямого провода длиной l = 80 см течет ток 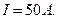Определить магнитную индукцию 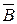поля, создаваемого этим током, в точке A, равноудаленной от концов отрезка провода и находящейся на расстоянии 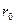= 30 см от его середины.

Решение. Для решения задач воспользуемся законом Био-Савара-Ла­пласа и принципом суперпо­зиции магнитных полей. Закон Био-Савара-Лапласа позволяет определить магнитную индукцию d 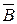, создавае­мую элементом тока I d . Заметим, что вектор d 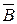в точ­ке А направлен за плоскость чертежа. Принцип суперпозиции позволяет для определе­ния 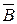воспользоваться геометрическим суммированием (интегрированием):

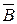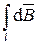= , (1)

где символ l означает, что интегрирование распространяется на всю длину провода.

Запишем закон Био-Савара-Лапласа в векторной форме:

,

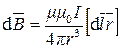где 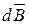– магнитная индукция, создаваемая элементом провода дли­ной 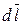с током I в точке, определяемой радиусом-вектором 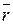; 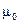– магнитная постоянная; 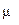– магнитная проницаемость среды, в кото­рой находится провод (в нашем случае 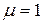). Заметим, что векторы 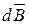от различных элементов тока сонаправлены (рис. 2), поэтому выраже­ние (1) можно переписать в скалярной форме:

,

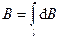где

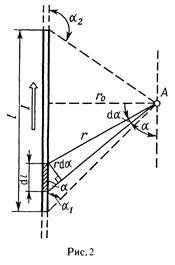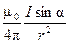d B = d l.

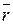В скалярном выражении закона Био-Савара-Лапласа угол α есть угол ме­жду элементом тока I d и радиусом-вектором . Таким образом,

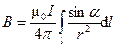(2)

Преобразуем подынтегральное выра­жение так, чтобы была одна перемен­ная – угол α. Для этого выразим длину элемента провода d l через угол

d α: d l = r d α /sin α (рис.2).

Тогда подынтегральное выраже­ние 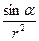d l запишем в виде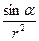 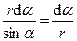. Заметим, что пере­менная 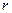также зависит от α, (r = r _o/sin 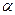); следовательно,

= .

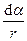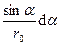Таким образом, выражение (2) можно пе­реписать в виде

,

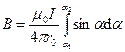где 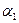и 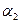– пределы интегрирования. Выполним интегрирование:

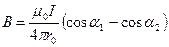. (3)

Заметим, что при симметричном расположении точки А относительно

отрезка провода 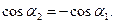С учетом этого формула (3) при­мет вид

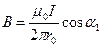. (4)

Из рис. 2 следует

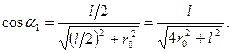
Подставив выражение cos 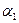в формулу (4), получим

. (5)

Произведя вычисления по формуле (5), найдем В = 26,7 мкТл.

Направление вектора магнитной индукции 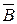поля, создаваемого пря­мым током, можно определить по правилу буравчика (правилу правого винта). Для этого проводим магнитную силовую линию (штриховая линия на рис. 3) и по касательной к ней в интересующей нас точке проводим вектор 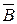. Вектор магнитной индукции 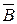в точке А (см. рис. 2) направлен перпендикулярно плоскости чертежа от нас.

Пример 2. По тонкому проводящему кольцу радиусом R=10 см течет ток I = 80 А. Найти магнитную индукцию 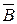в точке A, равноудален­ной от всех точек кольца на расстояние r =20 см.

Решение. Для решения задачи воспользуемся законом Био-Савара-Ла­пласа:

,

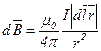где 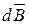– магнитная индукция поля, создаваемого элементом тока в точке, определяемой радиусом-вектором .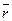

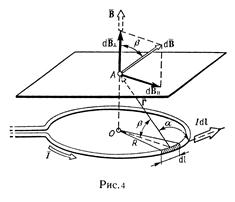
Выделим на кольце элемент 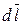и от него в точку А проведем радиус-вектор 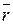(риc. 4). Вектор 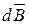направим в соответствии с пра­вилом буравчика.

Согласно принципу суперпозиции магнитных полей,

магнитная индукция 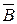в точке А определяется интегрированием

,

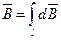где интегрирование ведется по всем элементам 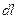кольца.

Разложим вектор 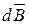на две составляющие: , перпендику­лярную плоскости кольца, и d 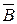_║ , параллельную плоскости кольца, т. е.

.

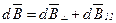Тогда

.

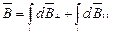Заметив, что 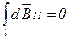из соображений симметрии и что векторы от различных элементов 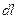сонаправлены, заменим векторное суммирование (интегрирование) скалярным:

,

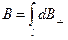где 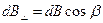и 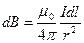(поскольку 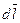перпендикуля­рен 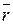и, следовательно, 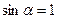). Таким образом,

.

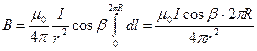После сокращения на 2π и замены cos β на (рис. 5) получим

Проверим, дает ли правая часть равенства единицу магнитной индукции (Тл):

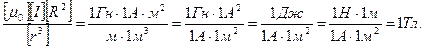
Здесь мы воспользовались определяющей формулой для магнитной индукции:

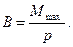
Тогда

.

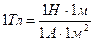Выразим все величины в единицах СИ и произведем вычисле­ния:

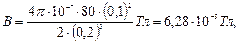
или В = 62,8 мкТл.

Вектор 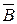направлен по оси кольца (пунктирная стрелка на рис. 4) в соответствии с правилом буравчика.

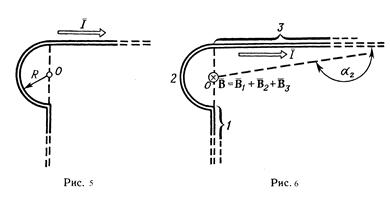
Пример 3. Бесконечно длинный провод изогнут так, как это изобра­жено на рис. 5. Радиус R дуги окружности равен 10см. Определить магнитную индукцию 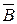поля, создаваемого в точке О током 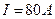, текущим по этому проводу.

Решение. Магнитную индукцию 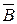в точке О найдем, используя прин­цип суперпозиции магнитных полей: 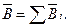В нашем случае про­вод можно разбить на три части (рис. 6): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружно­сти (2) радиуса R. Тогда

,

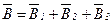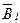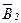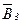где , и – магнитные индукции в точке О, создаваемые то­ком, текущим соответственно на первом, втором и третьем участках провода.

Так как точка О лежит на оси провода 1, то 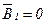и тогда

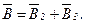
Учитывая, что векторы 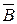₂ и 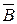₃ направлены в соответствии с прави­лом буравчика перпендикулярно плоскости чертежа от нас, то геомет­рическое суммирование можно заменить алгебраическим:

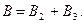
Магнитную индукцию В₂ найдем, воспользовавшись выраже­нием для магнитной индукции в центре кругового тока:

В нашем случае магнитное поле в точке О создается лишь половиной такого кругового тока, поэтому

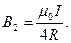
Магнитную индукцию В₃ найдем, воспользовавшись соотно­ше­нием (3), выведенным в примере 1:

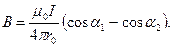
В нашем случае (), ,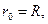

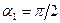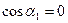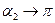
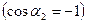тогда

Используя найденные выражения для В₂ и В₃, получим

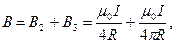
или

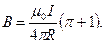
Произведем вычисления:

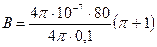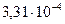Тл = Тл,

или

В = 331 мкТл.

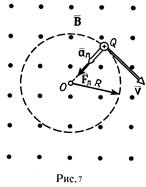Пример 4. Протон, прошедший ускоряю­щую разность потенциалов U = 600 В, вле­тел в однородное магнитное поле с индук­цией В = 0,3 Тл и начал двигаться по ок­ружности. Вычислить радиус R окружности.

Решение. Движение заряженной частицы в однородном магнитном поле будет происходить по окружности только в том случае, когда частица влетит в магнитное поле перпендикулярно линиям магнитной ин­дукции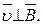

Так как сила Лоренца перпендикулярна вектору , то она сообщит частице (протону) нормальное ускорение .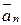

Согласно второму закону Ньютона,

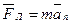, (1)

где m – масса протона.

На рис. 7 совмещена траектория протона с плоскостью чертежа и дано (произвольно) направление вектора . Силу Лоренца направим перпендикулярно вектору к центру окружности (векторы 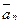и 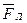сонаправлены). Используя правило левой руки, определим направле­ние магнитных силовых линий (направление вектора ).

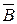Перепишем выражение (1) в скалярной форме (в проекции на радиус):

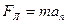. (2)

В скалярной форме 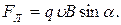В нашем случае 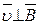и 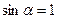, тогда Так как нормальное ускорение то выражение (2) перепишем следующим образом:

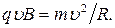
Отсюда находим радиус окружности

.

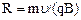Заметив, что 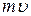есть импульс протона (p), это выражение можно записать в виде

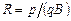. (3)

Импульс протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. 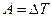, или

где 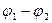– ускоряющая разность потенциалов (или ускоряющее напряжение U); Т₁ и Т₂ – начальная и конечная кинетические энергии протона.

Пренебрегая начальной кинетической энергией протона 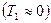и выразив кинетическую энергию Т₂ через импульс p, получим

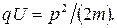
Найдем из этого выражения импульс 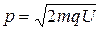и подставим его в формулу (3):

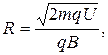
или

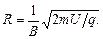(4)

Убедимся том, что правая часть равенства дает единицу длины (м):

Подставим в формулу (4) числовые значения физических вели­чин и произведем вычисления:

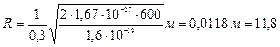мм.

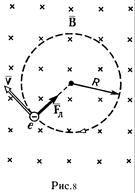Пример 5. Электрон, влетев в однородное магнитное поле (В = 0,2 Тл), стал двигаться по окружности радиуса R = 5см. Определить магнитный момент 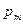эквивалентного кругового тока.

Ρ е ш е н и е. Электрон начинает двигаться по окружности, если он влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции. На рис.8 линии маг­нитной индукции перпендикулярны плоскости чертежа и направлены «от нас» (обозначены крестиками).

Движение электрона по окружности эквивалентно круговому току, который в данном случае определяется выражением

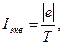
где 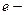заряд электрона; Т- период его обращения.

Период обращения можно выразить через скорость электрона 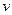и путь, проходимый электроном за период 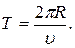Тогда

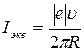. (1)

Зная 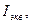найдем магнитный момент эквивалентного кругового тока. По определению, магнитный момент контура с током выражается со­отношением

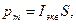(2)

где S – площадь, ограниченная окружностью, описываемой электроном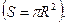

Подставив 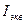из (1) в выражение (2), получим

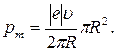
Сократим на и перепишем это выражение в виде

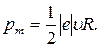(3)

В полученном выражении известной является скорость элек­трона, которая связана с радиусом R окружности, по которой он дви­жется, соотношением (см. пример 4). Заменив q на 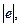найдем интересующую нас скорость 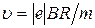и подставим ее в формулу (3):

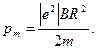
Убедимся в том, что правая часть равенства дает единицу маг­нитного момента :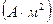

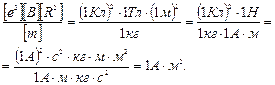
Произведем вычисления:

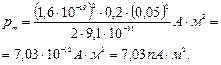
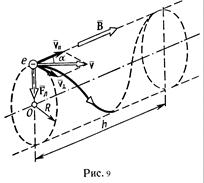
Пример 6. Электрон движется в однородном магнитном поле (В = 10 мТл) по винтовой линии, радиус R которой равен 1 см и шаг h = 6 см. Определить период Т обращения электрона и его скорость υ.

Решение. Электрон будет двигаться по винтовой линии, если он вле­тает в однородное магнитное поле под некоторым углом (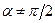) к линиям магнитной индукции. Разложим, как это показано на рис.9, скорость электрона на две составляющие: параллельную вектору 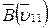и перпендикулярную ему (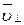). Скорость 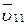в магнитном поле не изменяется и обеспечивает перемещение электрона вдоль си­ловой линии. Скорость 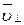в результате действия силы Лоренца будет изменяться только по направлению (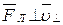) (в отсутствие парал­лельной составляющей (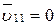) движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным сило­вым линиям). Таким образом, электрон будет участвовать одновре­менно в двух движениях: равномерном перемещении со скоростью 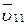и равномерном движении по окружности со скоростью .

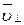Период обращения электрона связан с перпендикулярной со­ставляющей скорости соотношением

. (1)

Найдем отношение 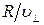. Для этого воспользуемся тем, что сила Лоренца сообщает электрону нормальное ускорение 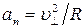. Согласно второму закону Ньютона можно написать

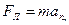или

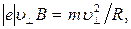(2)

где

Сократив (2) на выразим соотношение 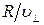(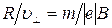) и подставим его в формулу (1):

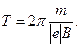
Убедимся в том, что правая часть равенства дает единицу вре­мени (с):

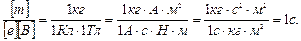
Произведем вычисления:

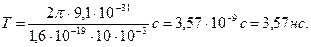
Модуль скорости 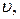как это видно из рис. 9, можно выразить через 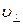и :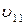

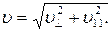
Из формулы (2) выразим перпендикулярную составляющую скорости:

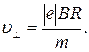
Параллельную составляющую скорости 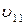найдем из следующих соображений. За время, равное периоду обращения Т, электрон прой­дет вдоль силовой линии расстояние, равное шагу винтовой линии, т.е. 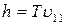, откуда

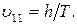
Подставив вместо Т правую часть выражения (2), получим

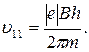
Таким образом, модуль скорости электрона

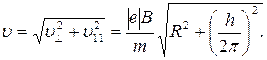
Убедимся в том, что правая часть равенства дает единицу скоро­сти (м/с). Для этого заметим, что R и h имеют одинаковую единицу – метр (м). Поэтому в квадратных скобках мы поставим только одну из величин (например, R):

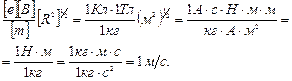
Произведем вычисления:

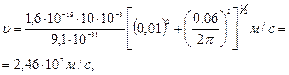
или 24,6 Мм/с.

Пример 7. Альфа-частица прошла ускоряющую разность потенциалов U = 104 В и влетела в скрещенные под прямым углом электрическое (Е = 10 кВ/м) и магнитное (В = 0,1 Тл) поля. Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим по­лям, частица не испытывает отклонений от прямолинейной траекто­рии.

Решение. Для того чтобы найти отношение заряда q альфа-частицы к ее массе m, воспользуемся связью между работой сил электрического поля и изменением кинетической энергии частицы:

откуда

. (1)

Скорость υ альфа-частицы найдем из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся за­ряженную частицу действуют две силы:

а) сила Лоренца 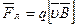, направленная перпендикулярно скоро­сти ν и вектору магнитной индукции ;

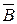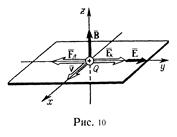
б) кулоновская сила 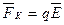, сонаправленная с вектором напряжен­ности 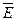электростатического поля (q>0). На рис. 10 направим вектор магнитной индукции 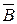вдоль оси Oz, скорость ν – в положительном направлении оси Оx, тогда 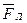и 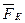будут направлены так, как показано на рисунке.

Альфа-частица не будет испытывать отклонения, если геометри­ческая сумма сил 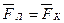будет равна нулю. В проекции на ось Оу получим следующее равенство (при этом учтено, что 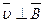и sin ):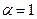

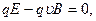
Дата добавления: 2014-12-08