Часть I. Надежность металлургических машин 1 страница

Раздел 1. Основы теории надежности

Глава 1. Основные понятия и определения

Теория надежности - это теория, которая устанавливает закономерности возникновения отказов объектов и методы их прогнозирования; изыскивает способы повышения надежности изделий при конструировании, изготовлении и поддержания их работоспособного состояния во время эксплуатации; разрабатывает методы контроля надежности изделий.

Под работоспособным состоянием объекта понимается такое состояние, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно-технической и (или) конструкторской документации.

Нарушение работоспособного состояния объекта является событием, получившим название отказ.

Отказы, по характеру своего проявления, подразделяются на:

- внезапные;

- постепенные.

Внезапный отказ - отказ, характеризующийся скачкообразным изменением значений одного или нескольких параметров объекта.

Постепенный отказ - отказ, обусловленный естественными процессами старения, изнашивания, коррозии и усталости при соблюдении всех установленных правил и (или) норм проектирования, изготовления и эксплуатации.

Отказы могут являться и являются следствием ошибок или недостаточного уровня знаний конструктора, или нарушения установленных правил и норм проектирования и конструирования. Такие отказы носят название конструктивные отказы.

Отказ, возникший по причине, связанной с несовершенством или с нарушением установленного процесса изготовления или ремонта, выполняемого на ремонтном предприятии, получил название производственный отказ.

Если нарушения установленных правил и (или) условий эксплуатации приводят к возникновению отказа, то такой отказ называется эксплуатационным отказом.

Для металлургических машин при пуске их в эксплуатацию наиболее характерными являются внезапные конструктивные отказы.

При установившемся процессе эксплуатации наиболее часто возникают внезапные эксплуатационные отказы.

Если прочностные свойства детали не изменяются, то внезапный отказ связан с перегрузкой. Если же в результате многократного воздействия предельных нагрузок происходит снижение прочностных свойств, то происходит внезапный отказ, связанный с развитием усталостных трещин.

Но внезапные отказы могут являться и следствием разброса механических свойств материала, из которого изготовлена деталь, и уровня нагрузок, действующих на нее (рис.1.1).

Если принять, что величины нагрузки и прочности подчиняются нормальному распределению (что во многих случаях соответствует действительности), то существует зона (на рис. 1.1 заштрихована) внезапных отказов при расчетном коэффициенте запаса прочности. Возникновение постепенных отказов в узлах трения вследствие развития процессов изнашивания протекает по схеме, представленной на рис.1.2.

Рис.1.1. Схема отказа при разбросе нагрузки

и прочностных свойств деталей

Первоначальный разброс величины зазора вследствие допуска на изготовление в процессе изнашивания увеличивается. Увеличение зазора определяется скоростью изнашивания J, величина которой имеет нормальное распределение, поэтому и наработки до отказа в этом случае имеют нормальное распределение.

В теории надежности при рассмотрении надежности объектов введены понятия "система" и "элемент".

Рис.1.2. Схема возникновения постепенных отказов:

[U]=U _max - максимально допустимая величина износа (отказ);

D - исходный зазор в соединении;

f (D) - плотность распределения зазора в соединении;

f (J) - плотность скорости изнашивания;

f (t)- плотность вероятности отказов;

Т - средняя наработка

Под системой будем понимать множество элементов и связь между ними, образующих некоторую целостность. Под элементом понимают часть системы, предназначенную для выполнения определенных функций и неделимую на составные части при данном уровне рассмотрения.

То есть только уровень рассмотрения определяет отнесение того или иного объекта, образующего некоторую целостность, к системе или элементу.

Например, линия привода горизонтальных валков может рассматриваться как элемент, входящий в систему, - рабочая клеть. В то же время линия привода горизонтальных валков может рассматриваться как система с входящими в нее элементами: узел валков, узел шпиндельного соединения, узел шестеренной клети, электропривод. Все зависит от того, какие задачи мы ставим при исследовании надежности того или иного объекта.

Как правило, при исследовании надежности металлургических машин в процессе эксплуатации в качестве элементов принимаются детали или узлы, которые подвергаются замене или восстановлению в процессе технического обслуживания или ремонта металлургических агрегатов.

Элементы и системы, которые в случае отказа заменяются новыми, называются невосстанавливаемыми.

Элементы и системы, которые в случае отказа подвергаются восстановлению, называются восстанавливаемыми.

Важнейшим понятием теории надежности является понятие наработка, под которым понимается продолжительность или объем работы. Различают наработку до отказа и наработку между отказами или наработку на отказ.

Наработка до отказа - наработка объекта от начала его эксплуатации до возникновения первого отказа.

Наработка между отказами (на отказ) - наработка объекта от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа. Относится только к восстанавливаемым объектам.

Глава 2. Показатели надежности

Для характеристики свойств надежности введены показатели надежности, которые подразделяются на единичные, характеризующие одно из свойств, составляющих надежность объекта, и комплексные, характеризующие несколько свойств, составляющих надежность объекта.

К показателям, характеризующим безотказность объекта, относятся:

– вероятность безотказной работы P (t);

– вероятность отказа Q (t);

– интенсивность отказов l (t);

– средняя наработка до отказа T;

– гамма-процентная наработка до отказа T_g;

– параметр потока отказов w (t);

– средняя наработка на отказ T.

Для характеристики долговечности объекта введены показатели:

– средний ресурс T _р ;

– гамма-процентный ресурс T_g;

– средний срок службы T _сл ;

– гамма-процентный срок службы T_g.

Ремонтопригодность характеризуется показателями:

– вероятность восстановления P (t_в);

– среднее время восстановления T_в;

– средняя трудоемкость восстановления Q_в.

К комплексным показателям надежности относятся:

- коэффициент готовности K_г;

- коэффициент оперативной готовности K_ог;

- коэффициент технического использования K_ти.

Глава 3. Надежность невосстанавливаемого элемента

3.1. Вероятность отказа и вероятность

безотказной работы

Будем считать, что время безотказной работы t (наработка) есть какая-то случайная величина x с функцией распределения F(t), для которой существует плотность f(t)=F’(t)=dF(t)/dt.

Функция распределения F(t)=P(x<t) есть вероятность того, что на интервале времени [0, t] произойдет отказ, или величина случайной наработки x будет меньше заданной величины t. Назовем функцию распределения вероятностью отказа и обозначим символом Q(t)

F(t)=Q(t)=P(x<t). (3.1)

Дополнительную вероятность

P(t)=1-Q(t)=P(x і t) (3.2)

будем называть вероятностью безотказной работы. Следовательно, вероятность безотказной работы есть вероятность того, что элемент будет работоспособным в заданный момент времени, или это есть вероятность того, что случайная величина наработки x будет больше заданного времени t.

Известно, что если случайная величина наработки x имеет плотность функции распределения f(t)=F’(t), тогда

(3.3)

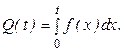
Плотность функции распределения* f(t) назовем плотностью вероятности отказов

(3.4)

.

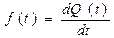Плотность вероятности отказов характеризуется вероятностью отказов в единицу времени на интервале [0, t].

На рис.3.1 показана графическая интерпретация представленных зависимостей.

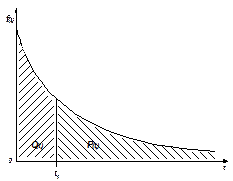
Рис.3.1. Плотность вероятности отказов:

Q(t₁) - вероятность отказа, численно равна площади под кривой плотности вероятности отказа, ограниченной справа ординатой, проведенной из точки, соответствующей моменту времени t₁;

P (t₁) -вероятность безотказной работы, численно равна площади под кривой плотности вероятности отказов, ограниченной слева ординатой, проведенной из точки, соответствующей моменту времени t₁

3.2. Интенсивность отказов

Примем, что на интервале времени [0, t] отказа не произошло. Необходимо выяснить, какова вероятность отказа в последующую единицу времени Dt (рис.3.2):

A - событие, в котором на интервале [0, t₁] не произошло отказа;

B - событие, в котором на интервале [t₁, t₂] произошел отказ;

С - событие, в котором на интервале [0, t₁] не произошло отказа, а на интервале [t₁, t₂] отказ произошел. Тогда

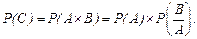
Рис.3.2. К расчету вероятности появления события C

В этом случае вероятность события C запишется как

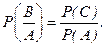(3.5)

Вероятность отказа машины в промежутке времени [t₁, t₂] можно выразить через вероятность безотказной работы

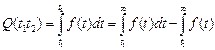
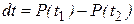. (3.6)

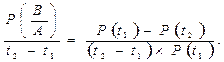Тогда вероятность того, что в этом интервале произойдет отказ за единицу времени t₂ - t₁ , при условии, что отказа не было до момента времени t₁, примет вид

(3.7)

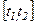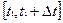Если записать интервал как , то

.

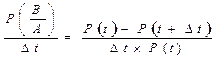Это соотношение характеризует ни что иное, как вероятность отказов за единицу времени на интервале [t_{2 –} t₁] при условии, что до момента времени t₁ отказа не было. То есть характеризует интенсивность отказов на интервале [t₁, t₂].

Мгновенное значение интенсивности отказов определяется как предел интенсивности отказов на интервале, когда длина интервала стремится к нулю

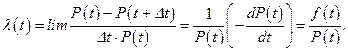(3.8)

И ее можно трактовать как вероятность того, что элемент, доживший до момента t, откажет за последующую (малую) единицу времени. Важность мгновенного значения интенсивности отказов состоит в том, что оно показывает изменение интенсивности отказов на протяжении срока службы некоторой совокупности объектов (механизмов, узлов, деталей).

Характерное изменение интенсивности отказов во времени представлено на рис. 3.3.

Рис.3.3. Интенсивность отказов за период службы машины

Для начального периода времени [0, t₁] характерны ранние отказы вследствие дефектов материала, конструкторских недоработок, дефектов изготовления. Этот отрезок кривой получил название период "детской смертности".

Второй отрезок кривой на интервале [t₁, t₂] отображает случайные внезапные отказы, вызванные неожиданным увеличением нагрузок, предельно тяжелыми условиями работы и т.д.

Отрезок кривой после момента времени t_2, характеризует старение объекта, являющееся следствием, как правило, проявления износовых отказов.

Иными словами, интенсивность отказов характеризует изменение качества изделия в процессе эксплуатации.

Интенсивность отказов связана с вероятностью безотказной работы соотношением

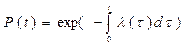, (3.9)

а с плотностью вероятности отказов соотношением

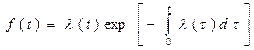. (3.10)

Интенсивность отказов, рассматриваемая на каком-то промежутке времени, называется накопленной интенсивностью отказов L(t) и связана с мгновенным значением интенсивности отказов соотношением

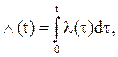(3.11)

а с вероятностью безотказной работы соотношением

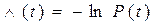. (3.12)

Найдем накопленную интенсивность отказов на интервале .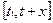

Из выражения (3.9) следует, что вероятность безотказной работы в момент времени t+x

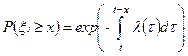, (3.13)

где 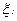- остаточное время жизни элемента, т.е. случайная величина, равная 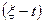при условии, что 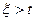; 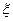- время безотказной работы элемента.

То есть вероятность отказа элемента, дожившего до момента времени t, на очередном интервале [t,t+x] зависит только от значения функции 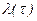на этом интервале и не зависит от ее поведения вне этого интервала и может характеризоваться накопленной интенсивностью отказов 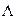(t,t+x) на интервале [t,t+x].

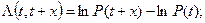
(3.14)

Пример 3.1. Долговечность комплекта вкладышей шпинделей со стороны валков в линии привода чистовой группы клетей (7 клетей) имеет нормальное распределение с математическим ожиданием m=60 сут и средним квадратичным отклонением 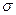=10 сут.

1. Построить график плотности распределения отказов и интенсивности отказов на интервале [0, 70 сут].

2. Определить возможное число n₁ отказавших комплектов вкладышей к моменту времени t=50 сут.

3. Определить возможное число отказавших комплектов вкладышей n₂ на интервале [50 - 60] сут.

4. Определить возможное число отказов вкладышей n₃ на интервале [50-60] сут, если до момента времени t=50 сут отказов не было.

Решение.

Построение графиков осуществим, используя зависимости:

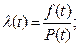
т.е.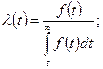

.

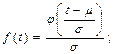
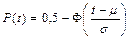Возможное число отказавших комплектов вкладышей n₁ для t=50, m=60 учитывая, что Q(t)=1-P(t) и Ф(-z)=-Ф(z):

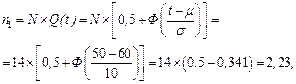
где N – число комплектов вкладышей в чистовой группе клетей со стороны валков;

Ф – нормированная функция Лапласа, т.е. функция распределения (см. табл. 1 прил.Б).

Возможное число отказавших комплектов вкладышей n₂ на интервале [50-60] сут, если были отказы в интервале [0-50] сут.

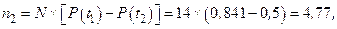
т.к. ,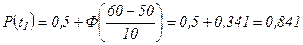

P(t₂)=0,5

Возможное число отказов комплектов вкладышей n₃ на интервале [50-60] сут, если до отказов не было, найдем, используя график интенсивности отказов на рис.3.4.

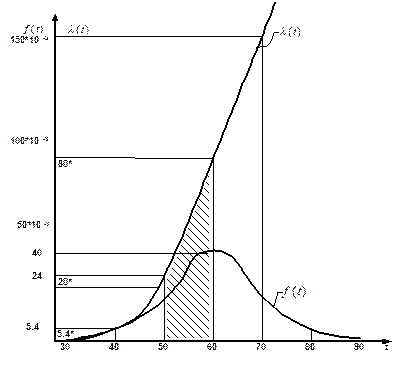
Рис.3.4. График плотности распределения отказов

и интенсивности отказов для условий примера 3.1

Площадь под кривой интенсивности отказов на интервале [50-60] сут есть вероятность отказов вкладышей на этом интервале при условии, что до этого отказов не было. Тогда возможное число отказов комплектов вкладышей n₃ при использовании накопленой интенсивности отказов, определенной по площади ограниченной кривой 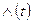, т.е. приближено в виде трапеции, будет равно

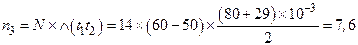
или, более точно, принимая во внимание формулу (3.12):

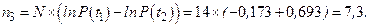
3.3. Средняя наработка до отказа и другие числовые

характеристики надежности

Очень часто на практике затруднительно оценивать надежность функциональными характеристиками, и в этом случае надежность элемента характеризуют числовыми характеристиками. Наиболее важными из них являются: среднее время безотказной работы (средняя наработка до отказа) 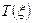и дисперсия 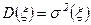, где 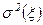- среднее квадратичное отклонение случайной величины :

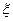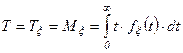; (3.15)

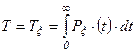; (3.16)

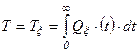; (3.17)

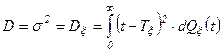; (3.18)

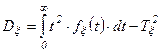. (3.19)

Следовательно, средняя наработка на отказ есть математическое ожидание Mx случайной величины наработки x, а дисперсия или среднее квадратичное отклонение служит мерой отклонения случайной величины наработки x от ее математического ожидания Mx или, что то же самое, от средней наработки Тx.

На рис.3.4. представлена графическая интерпретация средней наработки и среднего квадратичного отклонения.

Для характеристики степени разброса величин случайной наработки применяют коэффициент вариации, равный отношению среднего квадратичного отклонения к средней наработке:

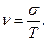(3.20)

Рис.3.4. Графическая интерпретация средней наработки:

Ц.Т. - центр тяжести площади сечения под кривой плотности

вероятности отказов

Значения случайной наработки x практически не выходят за пределы интервала [T±3s].

Это правило носит название “правило трех сигм”.

В ряде случаев для характеристики надежности изделия используют медианное* значение наработки Mex. Медиана - это квантиль порядка 0,5. Tо есть Mex - это значение наработки для вероятности безотказной работы P(t)=0,5.

Значения же наработки для любого заданного значения g в % вероятности безотказной работы получили название “гамма-процентной наработки T_g”.

Глава 4. Распределения, используемые в теории надежности

4.1. Распределения и область их применения

Для анализа надежности машин в процессе эксплуатации необходимо иметь сведения о наработках до отказа элементов, на основании которых осуществляют оценивание показателей надежности исследуемого объекта. Получение же оценок надежности основано на различных предположениях о законах распределения наработок до отказа.

Выдвижение гипотезы о принадлежности наработок к тому или иному распределению может основываться либо на изучении физики явлений, приводящих к отказу, либо на основе аналитического исследования статистических данных об отказах оборудования.

Исследование надежности металлургического оборудования показало, что наработки оборудования можно описать в большинстве случаев следующими распределениями:

- экспоненциальным (показательным);

- нормальным;

- логарифмически нормальным;

- Вейбулла.

Экспоненциальное распределение характерно для внезапных отказов, когда элемент не стареет, а также для отказов сложных технических систем независимо от причины их возникновения.

Нормальным распределением описываются наработки, длительность которых определяется процессами изнашивания (старения).

Логарифмически нормальное распределение точнее, чем нормальное, описывает наработки до отказа вследствие развития усталости, а также время восстановления работоспособности изделия.

Если элемент подвержен как внезапным, так и постепенным отказам, то наиболее приемлемым является распределение Вейбулла.

В каждом конкретном случае только на основании исследования характера повреждения можно принять решение о принадлежности полученных наработок к тому или иному распределению.

Например, мы исследуем надежность линии привода формирующего ролика моталки стана горячей прокатки полос.

Рис.4.1. Кинематическая схема линии привода

формирующего ролика моталки:

1 - карданный вал;

2 - подшипники качения;

3 - формирующий ролик

Опыт эксплуатации линии привода формирующего ролика показал, что отказы возникают по следующим причинам:

- износ бронзовых втулок в шарнире Гука;

- износ шлицевого соединения карданного вала;

- разрушение подшипника качения;

- износ бочки ролика;

- поломка цапфы ролика.

Примем в качестве элемента, надежность которого изучаем, ролик. В этом случае наиболее вероятным является предположение об использовании распределения Вейбулла, так как отказы ролика происходят как по износу бочки, так и по поломкам цапфы.

Для изучения надежности элемента - карданный вал - наиболее вероятным является использование нормального распределения.

Если же мы хотим исследовать надежность элемента - подшипника качения, то следует принять логарифмически нормальное распределение, так как его разрушение есть следствие развития усталостных трещин.

Исследование же надежности элемента - линии привода формирующего ролика – будет основываться на экспоненциальном распределении, так как это сложная техническая система.

Принимаемые решения (гипотезы) не являются окончательными и должны проходить проверку по критериям согласия*.

Распределения, используемые в теории надежности, называют законами надежности.

4.2. Экспоненциальный (показательный) закон

Так называют распределение (рис.4.2), для которого

(4.1)

Это однопараметрическое распределение с параметром l - интенсивность отказов. Ввиду своей простоты оно получило широкое распространение при исследованиях надежности машин. Но произвольное его использование может приводить к грубым ошибкам.

Для экспоненциального распределения:

плотность вероятности отказов

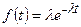; (4.2)

интенсивность отказов

l(t) = l = Const; (4.3)

числовые характеристики:

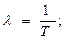
T = Mx; (4.4)

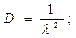
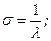
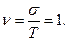
Коэффициент асимметрии A=2.

Эксцесс Е=6.

Характерным признаком экспоненциального распределения является равенство коэффициента вариации n единице. Экспоненциальное распределение является распределением без последствий, так как l = Const, т.е. вероятность отказа в каждую последующую единицу времени остается неизменной сколько бы ни проработал безотказно элемент до данного момента времени. Но необходимо отметить, что вероятность безотказной работы с течением времени снижается, т.е. чем дальше рассматривается момент времени от начала эксплуатации, тем меньше вероятность того, что объект будет находиться в работоспособном состоянии (см. рис.4.2).

Но если объект не отказал к рассматриваемому моменту времени, то вероятность его отказа в последующую единицу времени будет та же, что и в начальный момент эксплуатации.

Пример 4.1. Наработка пружин механизма уравновешивания верхнего шпинделя имеет экспоненциальное распределение со средней наработкой Т =40 сут.

Построить график плотности данного распределения и функцию распределения.

Решение.

Построение графиков осуществляем, используя формулы (4.1) - (4.3).

в

б

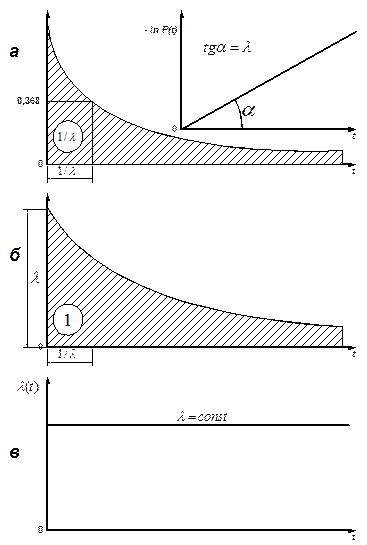
Рис.4.2. Экспоненциальное распределение:

a – вероятность безотказной работы;

б – плотность вероятности отказов;

в – интенсивность отказов

а

Плотность вероятности отказа (плотность функции распределения)

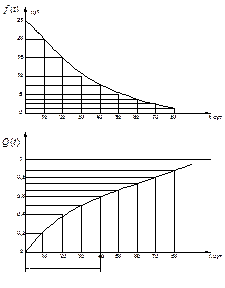
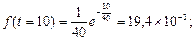
f(t=20)=15,2*10^-3;

f(t=30)=11,8*10^-3;

f(t=40)=9,2*10^-3;

f(t=50)=7,2*10^-3;

f(t=60)=5,6*10^-3;

f(t=70)=4,3*10^-3;

f(t=80)=3,4*10^-3.

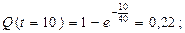
Плотность отказа (функция распределения)

Дата добавления: 2014-12-08