Часть I. Надежность металлургических машин 2 страница

Q(t=20)=0,393;

Q(t=30)=0,528;

Q(t=40)=0,632;

Q(t=50)=0,713;

Q(t=60)=0,777;

Q(t=70)=0,826;

Q(t=80)=0,865.

Пример 4.2. В линии привода формирующих роликов моталки происходят внезапные отказы роликов.

Определить, в какой момент времени может быть обеспечена вероятность безотказной работы P(t) = 0,8, если в межремонтный период t = 30 сут вероятность отказа Q(t) = 0,632.

Решение.

Из-за отсутствия другой информации предполагаем, что наработки роликов описываются экспоненциальным распределением (отказы происходят внезапно).

Для экспоненциального распределения значение Q(t) = 0,632 соответствует моменту времени, равному средней наработке:

t_p=T.

Для экспоненциального распределения

,

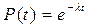отсюда

Тогда t=-30ln0,8 = 6,7 сут.

4.3. Нормальный закон

Нормальное распределение – это двухпараметрическое распределение (рис.4.3) с плотностью

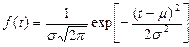, (4.5)

где m, s - параметры распределения.

Вероятность безотказной работы

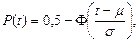(4.6)

где (t-m)/s = - квантиль нормированного распределения.

Вероятность попадания в интервал [a, b] выражается формулой

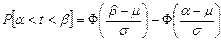. (4.7)

Свойства функции Лапласа Ф(x):

1. Ф(0) = 0; 2.Ф(-x)=- Ф(x); 3. Ф(± )=±0,5.

Интенсивность отказов

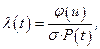(4.8)

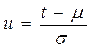
где (u) - табличное значение (см. табл.2).

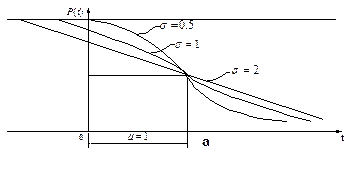
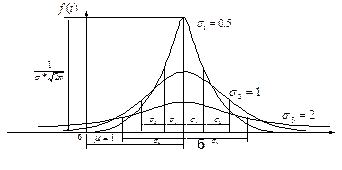
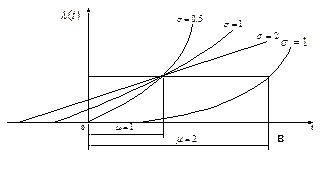
Рис.4.3. Нормальное распределение:

а – вероятность безотказной работы;

б – плотность вероятности отказов;

в – интенсивность отказов

Числовые характеристики распределения:

средняя наработка

T=Mx=m;

дисперсия

D=s²;

коэффициент вариации

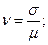
коэффициент асимметрии А =0;

эксцесс E =0.

Строго говоря, в теории надежности должен использоваться усеченный (слева) нормальный закон (рис.4.4) с плотностью

(4.9)

так как наработки являются неотрицательными величинам, где

(4.10)

Вероятность безотказной работы

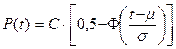
; (4.11)

Интенсивность отказов

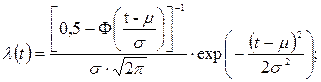. (4.12)

На графике рис.4.4 видно, что с увеличением срока эксплуатации интенсивность отказов растет, т.е. снижается надежность изделия.

Для усеченного нормального распределения при (m /s)>3 характеристики практически совпадают с нормальным распределением

m/s
C	1,189	1,023	1,001

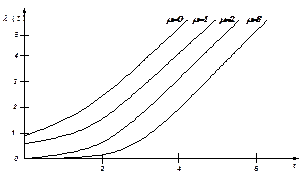
Рис.4.4. Усеченное (слева) нормальное распределение:

а -вероятность безотказной работы;

б – плотность вероятности отказов;

в – интенсивность отказов

Поэтому широко используются более простые зависимости нормального распределения для стареющих элементов.

Пример 4.3. Ролики транспортного рольганга имеют наработки, распределенные по нормальному закону с математическим ожиданием m =350 сут и средним квадратичным отклонением s=50 сут.

1. Найти вероятность безотказной работы роликов на 300 сут.

2. Построить график интенсивности отказов.

3. Если вероятность появления отказов в процессе эксплуатации не должна превышать 20%, то через какой период времени необходимо проводить их замену?

Решение.

Вероятность безотказной работы находим по формуле (4.6).

.

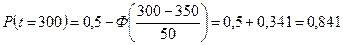Функцию Лапласа F((t-m)/s) находим из табл. 1 прил. Б для функции нормированного нормального распределения. Построение графика интенсивности отказов осуществляем, используя формулу (4.8).

Так как из условия задачи вероятность отказа Q(t)=0,2, то вероятность безотказной работы P(t)=0,8.

Тогда табличное значение квантили 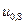нормального распределения равно (-0,842) из табл.3. прил.Б. Следовательно, замену роликов необходимо проводить через

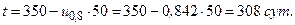
Пример 4.4. Наработки шарнира универсального шпинделя описываются нормальным распределением с математическим ожиданием m=40 сут и средним квадратичным отклонением s=20 сут.

Определить, при какой величине m (s=const) и при какой величине s (m=const) будет обеспечена в межремонтный период t_p=30 сут вероятность отказа Q (t=30)=0,1.

Решение.

Для обеспечения заданной вероятности отказа (табл.3, прил.Б), тогда

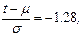
отсюда

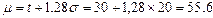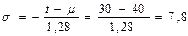сут;

сут.

Следовательно, для обеспечения вероятности безотказной работы P(t=30)=0,9 необходимо выполнить мероприятия либо по повышению средней наработки шарнира универсального шпинделя в 1,4 раза, либо по снижению стандарта до 7,8 сут.

Как правило, повышение средней наработки связано с существенными затратами, направленными на повышение износостойкости.

Величина среднего квадратичного связана с нарушениями технологического процесса получения материала, процесса изготовления изделия и правил его технической эксплуатации.

Поэтому достижение более низких значений среднего квадратичного является следствием не только чисто технических, но и организационных мероприятий.

4.4. Логарифмически нормальный закон

Логарифмически нормальное распределение – распределение двухпараметрическое (рис.4.5) с плотностью распределения

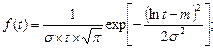(4.13)

где s и m - параметры распределения.

Вероятность безотказной работы

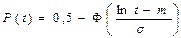. (4.14)

Интенсивность отказов

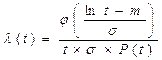. (4.15)

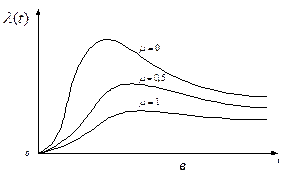
Рис.4.5. Логарифмически нормальное распределение:

а – вероятность отказов;

б – плотность вероятности отказов;

в – интенсивность отказов

Для логарифмически нормального распределения характерно возрастание интенсивности отказов с увеличением срока эксплуатации.

Числовые характеристики:

средняя наработка

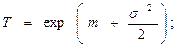(4.16)

дисперсия

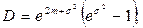(4.17)

коэффициент вариации

.

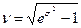Пример 4.5. Наработка до отказа подшипника скольжения механизма уравновешивания шпинделей имеет логарифмически нормальное распределение с параметрами m=4, s=1.

1. Найти вероятность безотказной работы и интенсивность отказов при наработке t =60 сут.

2. Определить величину средней наработки.

Решение.

Подставляя в формулу (4.14) численные значения m, s и t, получим

где Ф_(0,04)=0,036 из табл.1 прил.Б нормированного нормального распределения.

Используя выражение (4.15), находим интенсивность отказов.

,

где Ф_(0,04)=0,3973 из табл.2 прил.Б.

Значение величины средней наработки находим по формуле (4.16)

4.5. Закон Вейбулла

Закон Вейбулла - это двухпараметрическое распределение (рис.4.6) с плотностью отказов

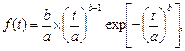(4.18)

где b - параметр формы; a - ресурсная характеристика.

Вероятность безотказной работы

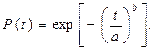(4.19)

Интенсивность отказов

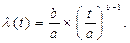(4.20)

Числовые характеристики:

средняя наработка

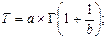(4.21)

дисперсия

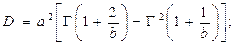(4.22)

коэффициент вариации

n

(4.23)

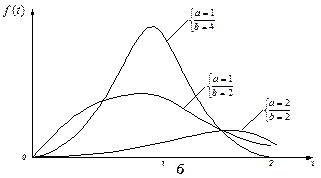
Рис.4.6. Распределение Вейбулла:

а – вероятность безотказной работы;

б – плотность вероятности отказов;

в – интенсивность отказов

Для закона Вейбулла интенсивность отказов имеет различный характер изменения с течением времени в зависимости от параметра b.

При b =1 интенсивность отказов есть величина постоянная и распределение Вейбулла переходит в экспоненциальное распределение.

Для b=2 распределение Вейбулла переходит в распределение Релея, и интенсивность отказов описывается уравнением прямой

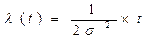. (4.24)

Для b>2 интенсивность отказов растет с течением времени. Если же b<1, интенсивность с течением времени снижается, что, как указывалось выше, характерно для начального периода эксплуатации новых изделий.

Пример 4.6. Наработка 7 секции транспортного рольганга имеет распределение Вейбулла с параметрами a=60 сут, b =l,9.

Найти вероятность безотказной работы и интенсивность отказов при наработке t= 40 сут.

Найти среднюю наработку на отказ.

Решение.

Подставляя исходные данные в формулу (4.19), получим

.

.

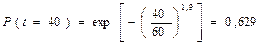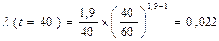Интенсивность отказов находим по формуле (4.20)

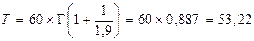Средняя наработка на отказ в соответствии с формулой (4.21)

сут.

где Г(1+1/1,9) - гамма-функция, значение которой находится из табл.6. прил.Б.

4.6. Непараметрические классы распределений наработки

Рассматривая вышеприведенные распределения, мы видели, что интенсивность отказов l(t) может быть как возрастающей, так и убывающей. Поэтому в основу классификационных признаков распределений наработки можно положить характер изменения интенсивности отказов. И в этом случае различают:

- распределения с возрастающей функцией интенсивности отказов (ВФИ - распределения);

- распределения с возрастающей в среднем функцией интенсивности отказов (ВСФИ - распределения').

В классе ВСФИ-распределений содержатся, например, усеченное нормальное, экспоненциальное, Вейбулла при значении параметра формы b>1.

ВФИ- и ВСФИ-распределения являются непараметрическими, когда неизвестен вид функции распределения – F(t).

Наработки можно отнести к классу ВСФИ при работе изделия в условиях ударных нагрузок. Предполагается, что система подвергается воздействию ударов, которые возникают случайным образом и вызывают повреждения (перегрузки) системы. Повреждения накапливаются до тех пор, пока не будет достигнут или превзойден некоторый критический уровень, при этом в системе наступает отказ (постепенный).

Упражнения

1. Средняя наработка подшипника скольжения уравновешивания шпинделей равна 44 сут. Вероятность безотказной работы в момент времени t=44 сут, P(t)=0,368.

Определить вероятность отказа в межремонтный период t_p=30 сут.

2. Секция транспортного рольганга содержит 20 роликов. Наработки роликов описываются распределением Вейбулла с параметрами a=150, b=2.

Определить возможное число отказов роликов:

а) на интервале [0, 120] сут;

б) на интервале [120, 150] сут;

в) на интервале [120, 150] сут при безотказной работе до момента времени t=120 сут.

3. Известно, что время восстановления работоспособности линии привода валков описывается логарифмически нормальным распределением m=0,5, s=0,2.

Определить среднее время восстановления работоспособного состояния и вероятность восстановления работоспособного состояния за 2 ч.

4. Зубчатые муфты распределительного редуктора в количестве 5 шт. выходят из строя по износу. Известно, что их средняя наработка T=100 сут, стандарт. s=30 сут.

Определить возможное число отказов муфт в межремонтный период t=60 сут.

5. По условиям примера 4 определить возможное число отказов муфт в следующий межремонтный период, если принято решение не проводить текущий плановый ремонт.

6. Наработки секции транспортного рольганга описываются распределением Вейбулла с параметрами a=60, b=2,0. В межремонтный период t_p=60 сут отказов не было. Было принято решение не проводить плановый ремонт.

Определить вероятное число отказов секции в следующий межремонтный период.

7. По условиям примера 6 определить величину средней наработки и интенсивность отказов в конце межремонтного периода.

8. По условиям примера 6 найти показатели безотказности в момент времени t=50 сут.

9. Наработка пружин механизма уравновешивания верхнего шпинделя описывается экспоненциальным распределением с параметром l=0,025.

В какой момент времени с начала эксплуатации вероятность безотказной работы будет равна 0,8 и какова вероятность отказа в данный момент времени?

10. Наработки подшипников качения механизма уравновешивания шпинделей описываются логарифмически нормальным распределением с параметрами m=5,5, s=1.

Найти интенсивность отказов в момент времени t=60 сут и вероятность отказа на интервале [60, 90] сут.

11. Карданные валы формирующих роликов моталки имеют ресурсную характеристику а=80 (сут) и коэффициент вариации n=0,6. Межремонтный период t=30 сут.

- определить вероятность отказа в межремонтный период

- определить вероятность отказа на 30 сутки

- определить возможное число отказов в следующий межремонтный период, если в предыдущем отказов не было.

Глава 5. Надежность восстанавливаемого элемента

Значительная часть элементов металлургического оборудования при отказах не заменяется на новые, а восстанавливается.

В качестве примера рассмотрим линию привода прокатных валков, включающую узел валков, узел шпиндельного соединения, шестеренную клеть.

Линия привода, принятая за элемент при анализе надежности, является восстанавливаемым элементом, так как любой отказ устраняется путем замены либо конкретной детали, либо узла, в состав которого входит отказавшая деталь. Если же линию привода при анализе надежности считать системой, а входящие в нее узлы - элементами и отказы устраняются путем замены узлов, то такая система называется восстанавливаемой, а элементы (узлы) - невосстанавливаемыми.

Например, при износе вкладышей универсального шпинделя происходит замена шпинделя в сборе. Шпиндель в сборе принят за элемент.

Возможен вариант, когда отказы устраняются путем восстановления элемента (узла), а не его заменой. Например, в элементе (узел шпинделя) заменяются вкладыши. Тогда такой элемент называется восстанавливаемым.

При анализе надежности восстанавливаемого элемента рассматриваются два случая:

- мгновенное восстановление (когда время восстановления мало и им можно пренебречь);

- конечное время восстановления.

Будем различать два типа восстановления - замену и ремонт. Предполагаем, что восстановление полное, т.е. после восстановления элемент имеет такую же надежность, что и в начальный момент.

5.1. Восстанавливаемый элемент

в случае мгновенного восстановления

Рассмотрим случай мгновенного восстановления.

Пусть 0<t₁<t₂<…..<t_n - последовательные моменты отказов (и восстановлений) элемента, a x₁=t₁; x₂=t₂-t₁;_……x_n=t_n-t_n-1…- время безотказной работы до первого отказа, после первого восстановления, второго восстановления и т.д.

Последовательность случайных моментов t₁, t₂,… t_n называют процессом восстановления, а раздел теории надежности, в котором изучается этот процесс, называют теорией восстановления.

Характеристики процесса восстановления являются характеристиками надежности восстанавливаемого объекта. Основные из этих характеристик следующие:

- число отказов до момента t - n (t), имеющее распределение:

(5.1)

где

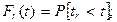
- функция восстановления (поток отказов) - среднее число отказов до момента t - H(t), W(t):

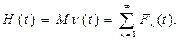(5.2)

Отсюда среднее число отказов на интервале [t₁ t+ x] равно

H(t+x)-H(t);

- интенсивность отказов (плотность восстановления) – h(t), w(t)

. (5.3)

Интенсивность отказов (параметр потока отказов) имеет двойной смысл.

С одной стороны, h(t) есть среднее число отказов за малую единицу времени, следующую за моментом t. С другой стороны, h(t) есть вероятность отказа за малую единицу времени;

- остаточное время жизни – x_t – это интервал от момента t до ближайшего справа отказа.

Как известно, наработки на отказ сложных технических систем распределены по экспоненциальному закону.

В этом случае число отказов в интервале продолжительностью t является случайной величиной, распределенной по закону Пуассона. Процесс восстановления будет пуассоновским процессом.

Во многих случаях восстанавливаемый элемент функционирует в течение времени t, которое во много раз больше средней наработки на отказ. В этом случае среднее число отказов на интервале [0, t] приближенно равно

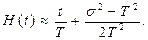(5.4)

Если элемент восстанавливается путем замены входящей в его состав отказавшей части (например, вкладыш в шпиндельном соединении) и функционирует время t, то n(t)Јn₀ есть число запасных элементов, необходимых для непрерывной работы элемента до момента t. Тогда

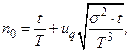(5.5)

где u_q - квантиль берется из табл.1 прил.Б, .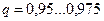

Среднее остаточное время

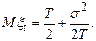(5.6)

Пример 5.1. Восстановление работоспособного состояния шпиндельного соединения осуществляется путем замены комплекта изношенных вкладышей со средней наработкой Т=46 сут и среднеквадратичным отклонением s=14 сут.

Определить среднее число замен, необходимых для непрерывной работы шпиндельного соединения в течение года и в течение месяца.

Решение.

Подставляя исходные данные в формулу (5.5), получим

;

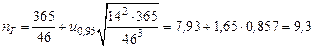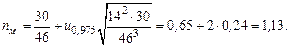
Значение квантили u_q находим из табл.3, прил.Б.

5.2. Распределение Пуассона

Распределение Пуассона является дискретным (рис.5.1) с распределением

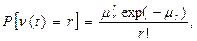(5.7)

где m_r=lt.

При m® распределение Пуассона приближается к нормальному (см. рис.5.1).

Среднее число отказов до момента времени t

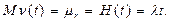(5.8)

Интенсивность отказов

h(t)=l, (5.9)

т.е. среднее число событий, появляющихся в единицу времени, есть величина постоянная.

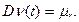Дисперсия

Коэффициент асимметрии

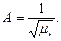
Эксцесс .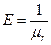

Коэффициент вариации

.

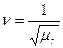Параметр пуассоновского распределения m_r. равен одновременно математическому ожиданию и дисперсии случайной величины.

Распределение Пуассона позволяет подсчитать вероятность отказов менее r, или равных r, за определенный промежуток времени:

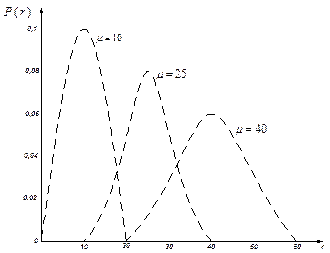
Рис.5.1. Распределение Пуассона

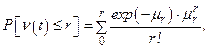(5.10)

и вероятность отказов более r:

. (5.11)

Данные зависимости можно использовать для определения гарантированного количества запасных частей, предотвращающее их истощение за определенный промежуток времени.

Пример 5.2. По данным примера 5.1. определить гарантированное количество запасных частей на 1 месяц.

Решение.

Определяем вероятность того, что за месяц потребуется не более одной замены (r=1).

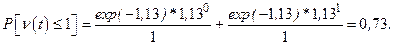
Из примера 5.1 m_r=1,13.

То есть вероятность того, что потребуется только одна замена, не так высока и существует риск, равный 27%, что одного комплекта вкладышей окажется недостаточно для обеспечения работоспособного состояния.

Определим вероятность появления за месяц более 2 отказов:

То есть остается риск, равный 6%, что наличие двух комплектов вкладышей не обеспечит гарантированное работоспособное состояние.

При наличии 3 комплектов вероятность их истощения равна 0:

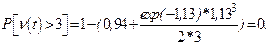
Поэтому возможная политика пополнения запасных комплектов вкладышей может состоять в следующем: с учетом времени на изготовление вкладышей создается их полугодовой запас в количестве 5 комплектов (см. пример 5.1). В дальнейшем не допускается снижение запаса комплектов вкладышей менее 3.

В общем случае принятие риска в 27, 6 или 0% определяется экономической составляющей потерь производства и требует соответствующего обоснования.

Пример 5.3. Наработки 6-й секции транспортного рольганга подчиняются экспоненциальному закону с параметром l =0,016.

1. Определить вероятность появления хотя бы одного отказа за 120 сут.

2. Определить вероятность появления за этот же срок не менее 2-х отказов.

Решение.

Если наработка на отказ имеет показательное распределение, то число отказов в заданном интервале описывается распределением Пуассона.

Подставляя исходные данные в формулу (5.10), получим значение вероятности появления хотя бы одного отказа

.

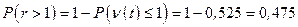Вероятность появления не менее 2-х отказов получим из формулы (5.11).

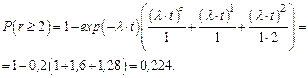
Значение P(n(t)=n) можно находить из табл.7 прил.Б.

5.3. Восстанавливаемый элемент

с конечным временем восстановления

Предположим, что время восстановления элемента конечно и им пренебречь нельзя. Тогда последовательные интервалы безотказной работы, как и в предыдущем случае (мгновенное восстановление), обозначим через x₁, x₂,…x_n, а последовательные участки восстановления через h₁, h₂,…h_n.

Предполагаем, что все величины x_i и h_i независимы в совокупности:

P(x _i<t)=Q(t); Mx _i=T₁; Dx _i=s₁²;

P(h _i<t)=G(t); Mh _i=T₂; Dh _i=s₂².

В этом случае моменты отказов и моменты восстановлений не совпадают. Обозначим число отказов до момента t -n₁(t), число восстановлений до момента t - n₂(t). Тогда среднее число отказов и восстановлений

Дата добавления: 2014-12-08