Часть I. Надежность металлургических машин 3 страница

H₁(t)=Mn₁(t); H₂(t)=Mn₂(t).

Эти величины могут описываться формулами, аналогичными формулам предыдущего параграфа.

Остаточное время x_t определяется здесь несколько иначе:

x_t =0, если момент t попал на участок восстановления; в противном случае x_t есть время до первого после момента t отказа.

Тогда

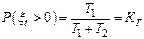(5.13)

есть величина, называемая коэффициентом готовности, характеризующая вероятность того, что в наугад взятый момент в стационарном режиме элемент будет исправен.

Для элемента с конечным временем восстановления важную роль играет еще одна характеристика, которую обычно называют суммарной наработкой S_t, - суммарное время работы элемента до момента t

(5.14)

Пусть h_x есть момент, в который суммарная наработка достигнет величины x, тогда справедлива следующая формула:

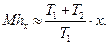(5.15)

Пример 5.4. Средняя наработка линии привода валков прокатной клети Т = 30 сут. Среднее время восстановления работоспособного состояния линии привода валков T₂ = 0,1 сут.

Определить коэффициент готовности линии привода валков.

Решение.

Коэффициент готовности определяем по формуле (5.13).

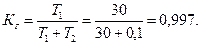
Упражнения

1. Отказы в секции транспортного рольганга, состоящей из 20 роликов, происходят с интенсивностью l=0,04=const. Восстановление работоспособного состояния осуществляется путем замены ролика в сборе. Межремонтный период t_р=30 сут.

Определить вероятность появления хотя бы одного отказа в этот период. Определить вероятность появления одного отказа за тот же период.

2. Отказы в механизме уравновешивания шпинделей связаны с поломкой пружин и описываются экспоненциальным распределением с параметром l=0,05. Межремонтный период t_р=30 сут.

Определить необходимое количество пружин на год.

3. Отказы шарнира универсальных шпинделей рабочей клети прокатного стана описываются распределением Вейбулла с параметрами a=80 сут, b=3. Восстановление работоспособного состояния осуществляется путем замены комплекта вкладышей.

Определить необходимое количество комплектов вкладышей на 1 месяц.

4. В результате осуществления технических мероприятий было достигнуто повышение средней наработки комплекта вкладышей (данные примера 3) в 2 раза. Коэффициент вариации остался неизменным. Стоимость комплекта вкладышей возросла в 1,5 раза.

Определить, является ли эффективным проведенное мероприятие (без учета затрат на замену и потерь производства).

5. Для условий примера 3 затраты на восстановление работоспособного состояния шарнира универсального шпинделя составляют 10 усл.ед., потери производства 15 усл.ед. Стоимость комплекта вкладышей 200 усл.ед.

Определить, какие расходы можно понести на проведение мероприятий:

а) по повышению средней наработки в 2 раза.

и неизменном коэффициенте вариации.

б) по снижению коэффициента вариации в 2 раза

и неизменной средней наработки.

6. Наработки подшипника скольжения механизма уравновешивания шпинделей описываются экспоненциальным распределением с параметром l=0,02.

Установить, на сколько должна быть повышена средняя наработка до отказа, чтобы снизить расход подшипников за год в 2 раза.

7. Для условий примера 6 определить вероятность безотказной работы подшипника скольжения в межремонтный период t_р=60 сут до и после повышения средней наработки.

8. Средняя наработка комплекта вкладышей шарниров универсальных шпинделей линии привода валков Т=50 сут. Межремонтный период t=30 сут.

Определить гарантированное количество комплектов вкладышей на межремонтный период.

9. Ходовые колеса (в количестве 8 колес) механизма передвижения моста крана имеют среднюю наработку T=600 сут. Нижняя, доверительная граница средней наработки Т=500 сут при доверительной вероятности q=0,95.

Определить необходимое количество запасных колес на 1 год.

10. Медианное значение наработки подшипников скольжения в механизме уравновешивания шпинделей прокатки t=60 сут. Коэффициент вариации n=0,35. Межремонтный период t=30 сут.

Определить необходимое количество запасных подшипников скольжения на межремонтный период.

Глава 6. Надежность систем

Надежность систем определяется надежностью входящих в ее состав элементов. При оценке надежности системы важно выяснить влияние на вероятность ее безотказной работы:

- количества входящих в нее элементов;

- вероятности безотказной работы элементов;

- способов соединения элементов в системе.

Элементы в системе могут иметь соединение последовательное, параллельное, смешанное.

При анализе надежности системы рассматривается ее структура, представленная в виде блок-схемы.

В качестве примера рассмотрим линию привода валков прокатной клети (рис.6.1)

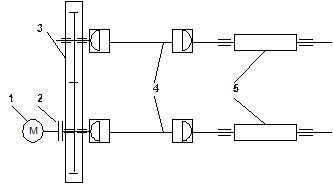
Рис.6.1. Кинематическая схема линии привода валков: 1 - электродвигатель; 2 - муфты; 3 - шестеренная клеть; 4 - шпиндели; 5 - рабочие валки

В этом случае блок-схема может быть представлена в виде последовательно соединенных элементов (рис.6.2).

Рис.6.2. Блок-схема линии привода валков.

Последовательное соединение

Если же предположить, что возможно осуществление процесса прокатки через привод одного валка, то блок-схема будет представлена в виде последовательно-параллельного соединения элементов (рис.6.3).

Рис.6.3. Блок-схема линии привода валков.

Смешанное соединение

6.1. Система с последовательным соединением элементов

Система с последовательным соединением элементов является наиболее распространенной для металлургических машин и наиболее простой для анализа надежности. Для такой системы при известной вероятности безотказной работы элементов P_i вероятность ее безотказной работы P_s находится из зависимости

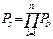(6.1)

где правая часть представляет собой произведение вероятностей безотказной работы элементов.

К сожалению, надежность такой системы быстро убывает при увеличении числа последовательно соединенных элементов; надежность системы всегда меньше надежности наименее надежного входящего в ее состав элемента.

Рассмотренная нами выше модель относится к состоянию системы в определенный момент времени (в статике).

Определим вероятность безотказной работы системы изменяющейся с течением времени.

Если x_i - случайная величина, обозначающая наработку до отказа i-го элемента, то вероятность безотказной работы системы, состоящей из n последовательно соединенных элементов, равна

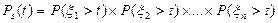
или

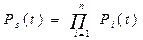, (6.2)

где P_i(t) - вероятность безотказной работы i-го элемента.

Интенсивность отказов системы l_s(t) находится из зависимости

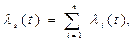(6.3)

где l_i(t) - интенсивность отказов i-го элемента.

Таким образом, при допущении о независимости отказов элементов интенсивность отказов системы равна сумме интенсивностей отказов отдельных элементов при любом распределении наработки элементов до отказа.

6.2. Система с параллельным соединением элементов

Система с параллельным соединением элементов - это такая система, которая не выходит из строя, пока не отказали все ее элементы. Блок-схема такой системы представлена на рис.6.4.

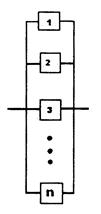
Рис.6.4. Блок-схема системы с параллельным соединением элементов

Вероятность безотказной работы системы P_s с параллельным соединением элементов с вероятностью безотказной работы P_i находится из зависимости

(6.4)

При анализе системы с параллельным соединением элементов подразумевается, что при включении системы включаются все элементы и что отказы не влияют на надежность элементов, продолжающих работать.

6.2.1. Система с нагруженным резервом

Параллельное соединение возникает обычно тогда, когда все элементы выполняют одну и ту же функцию. Для ее выполнения достаточно одного элемента, остальные играют роль резервных. Такой тип резервирования называют горячим или нагруженным резервом. В такой ситуации элементы, как правило, бывают одинаковыми и имеют равную надежность. Вероятность безотказной работы такой системы

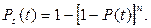(6.5)

Средняя наработка системы в случае экспоненциального распределения

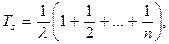(6.6)

где n - число элементов в системе.

Если каждый элемент имеет экспоненциальное распределение наработки и одинаковую интенсивность отказов, то вероятность безотказной работы системы для n=2 (дублирование) найдем из зависимости

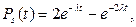(6.7)

а средняя наработка системы до отказа

(6.8)

6.2.2. Система с ненагруженным резервом

Система с ненагруженным резервом представляет систему с параллельным соединением элементов, в которой в каждый момент времени работает только один элемент; если работающий элемент выходит из строя, то включается другой элемент. Блок-схема системы с ненагруженным резервом показана на рис.6.5.

Примером такой схемы являются циркуляционные смазочные системы, в которых используется резервная маслонасосная станция, подключаемая в момент отказа основной станции.

Рассмотрим надежность таких систем при допущении безотказной работы переключателя и постоянной интенсивности отказов элементов.

В общем случае для n резервных элементов

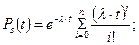(6.9)

Для наиболее распространенного случая при дублировании, когда n=1 (один резервный элемент):

(6.10)

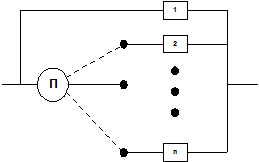
Рис.6.5. Блок схема системы с ненагруженным резервом

Если же возможны отказы переключателя с интенсивностью отказов l_n, то для системы с n=2 (дублирование) и постоянной интенсивностью отказов элементов

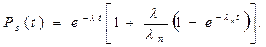(6.11)

Рассмотрим влияние на надежность системы различных схем включения, входящих в ее состав элементов.

Пример.6.1. Проанализировать надежность системы из 4-х элементов с различными схемами дублирования (резервирования), если вероятность безотказной работы элементов P(t)=0,9 с интенсивностью отказов l=0,004.

Решение.

Система, состоящая из четырех элементов с последовательным соединением, имеет вероятность безотказной работы в соответствии с формулами (6.2) и (6.3)

;

.

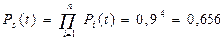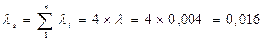Введем резервную систему с такими же параметрами и показателями надежности, как и основной системы, тогда

,

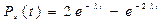так как интенсивность отказов - величина постоянная и мы имеем дело с экспоненциальным распределением.

Найдем момент времени, в котором элемент будет работоспособным с вероятностью P(t)=0,9.

P(t)=e^-lt; для P(t)>0,9 P(t)=1-lt.

Тогда

,

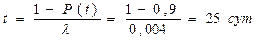а вероятность безотказной работы системы с нагруженным резервом

.

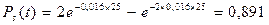Средняя наработка до отказа такой системы составит

,

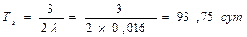тогда как для элемента средняя наработка до отказа будет равна

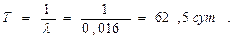
Осуществим ненагруженное резервирование системы.

Для случая безотказной работы переключателя вероятность безотказной работы системы по формуле (6.10) составит

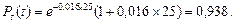
Если же принять, что возможен отказ переключателя с интенсивностью отказов l_п=0,001, то тогда вероятность безотказной работы системы по формуле (6.11) будет равна

.

Кроме резервирования системы в целом, можно осуществлять резервирование элементов, входящих в систему. Для этого случая вероятность безотказной работы системы в соответствии с формулами (6.2) и (6.7) будет равна

.

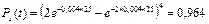При дублировании элементов системы ненагруженным резервом с безотказно работающим переключателем по формулам (6.1) и (6.12) вероятность безотказной работы составит

Если принять, что переключатель работает с интенсивностью отказов l_п=0,001, то вероятность безотказной работы такой системы, в соответствии с формулами (6.1) и (6.12), будет равна

Таким образом, параллельное подсоединение элементов или систем является эффективным средством повышения надежности машин. Наиболее эффективно дублирование элементов. Но эту возможность очень сложно реализовать в конкретных механических системах. И тем не менее, резервирование – наиболее распространенный способ повышения надежности металлургического оборудования (циркуляционные смазочные системы, механизм главного подъема разливочных кранов, три-пять моталок на широкополосных станах горячей прокатки и т.д.).

Другим направлением повышения надежности машин является конструирование машин на нагрузки, превышающие эксплуатационные, т.е. путем введения избыточности оборудования сверх необходимого количества.

Так, например, при наличии в чистовой группе 8 рабочих клетей при отказе одной из клетей возможно перераспределение обжатий и осуществление процесса прокатки на 7 клетях.

Упражнения

1. Двухклетевой дрессировочный стан включает разматыватель и моталку. Интенсивность отказов клетей 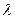_кл=0,02, разматывателя 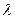_р=0,03, моталки 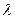_м=0,01.

Определить вероятность отказа стана в межремонтный период t_р=30 сут.

2. По условиям примера 1 определить показатели безотказности стана (Т,Р(t=30))при:

а) ненагруженном резервировании разматывателя;

б) ненагруженном резервировании моталки;

в) ненагруженном резервировании моталки и разматывателя.

Сделать заключение об эффективности резервирования.

3. Секция транспортного рольганга, включающая 20 равнонадежных роликов, имеет интенсивность отказа 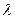=0,02. Отказ 1 ролика приводит к отказу всей секции.

Определить среднюю наработку роликов (в случае экспоненциального распределения).

4. Для условий примера 3 определить вероятность нахождения ролика в работоспособном состоянии через 180 сут и вероятность безотказной работы в 180-е сутки.

5. Для условий примера 1 ввели ненагруженное резервирование разматывателя. Как изменится вероятность безотказной работы стана в межремонтный период?

6. Для условий примера 5 на стане были проведены мероприятия по повышению средней наработки на отказ разматывателя в 2 раза. Как изменится в этом случае вероятность безотказной работы стана в межремонтный период?

7. Средняя наработка на отказ системы, состоящей из 3-х равнонадежных элементов, равна 100 сут.

Найти межремонтный период, если известно, что вероятность отказа за этот период равна 0,2.

Как изменится средняя наработка на отказ системы, если один из элементов будет продублирован?

8. Система, состоящая из 4-х равнонадежных элементов, в момент времени t будет находиться в работоспособном состоянии с вероятностью 0,8.

Определить этот момент времени, если интенсивность отказов каждого элемента равна 0,004, и как изменится Р(t), если один из элементов будет продублирован.

Глава 7. Ремонтопригодность машин

Затраты на поддержание оборудования в работоспособном состоянии во многом зависят от его надежности, одним из свойств которой является ремонтопригодность.

Ремонтопригодностью определяется свойство машин, которое способствует предупреждению и обнаружению причин возникновения отказов, восстановлению работоспособного состояния путем проведения технического обслуживания и ремонтов.

Ремонтопригодность, как свойство машины, закладывается при конструировании. Уже на стадии конструирования в машину должны быть заложены возможности по предупреждению и обнаружению отказов (системы технической диагностики, системы контроля параметров, определяющих работоспособность оборудования), а также обеспечена возможность минимальных затрат времени и трудовых ресурсов на восстановление работоспособности машины.

Таким образом, мерой ремонтопригодности являются время и затраты на восстановление работоспособного состояния.

К сожалению, во многих конструкциях металлургических машин вопросы их ремонтопригодности проработаны очень слабо и имеют низкие показатели.

Ремонтопригодность характеризуется как единичными, так и комплексными показателями.

Единичные показатели:

1. Среднее время восстановления работоспособного состояния (математическое ожидание времени восстановления работоспособного состояния) – .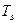

2. Вероятность восстановления работоспособного состояния - 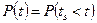(вероятность того, что время восстановления работоспособного состояния не превысит заданного - аналогия вероятности отказа).

3. Средние затраты на восстановление работоспособного состояния - .

Комплексные показатели:

1. Коэффициент готовности - 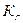. Вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается.

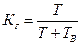, (7.1)

где Т - средняя наработка на отказ.

2. Коэффициент оперативной готовности - 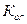. Вероятность безотказной работы объекта в течение заданного времени t, начиная с произвольного, достаточно удаленного момента времени tҐ.

Оценкой 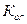является отношение

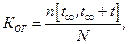(7.2)

т.е. отношение числа объектов, исправных в произвольный, достаточно удаленный момент времени и проработавших затем безотказно в течение заданного времени t, к общему числу объектов.

3. Коэффициент технического использования - .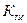

(7.3)

Отношение средней наработки на отказ за некоторый период эксплуатации к сумме средних наработок на отказ, длительности плановых ремонтов и аварийных простоев оборудования.

Этими показателями оценивается ремонтопригодность машин в процессе их эксплуатации.

Для оценивания же ремонтопригодности машин на стадии проектирования используются относительные показатели ремонтопригодности:

· коэффициент взаимозаменяемости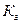

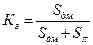; (7.4)

· коэффициент доступности

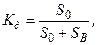(7.5)

где 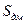- трудоемкость демонтажно-монтажных работ, чел.-ч/ед. наработки;

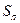- трудоемкость пригоночных работ, чел.-ч/ед. наработки;

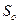- трудоемкость основных операций, чел.-ч/ед. наработки;

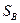- трудоемкость вспомогательных операций, чел.-ч/ед. наработки;

· коэффициент унификации

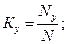(7.6)

· коэффициент стандартизации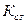

, (7.7)

где , 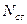- число соответственно унифицированных и стандартных сборочных единиц или деталей, не вошедших в состав сборочных единиц;

N - общее число составных частей.

При оценке ремонтопригодности новых конструкций машин используется и качественная или экспертная оценка. При экспертной оценке ремонтопригодности выделяют параметры, определяющие трудоемкость и длительность восстановления.

Такими параметрами могут являться:

· количество сборочных единиц;

· количество предварительно снимаемых элементов для доступа к месту отказа;

· технологичность процесса сборки;

· рабочие позы ремонтников;

· возможность использования средств механизации;

· наличие средств контроля и систем технической диагностики;

· организация технического обслуживания и ремонтов.

Оценивание параметров может осуществляться либо в баллах, либо словами: «лучше», «хуже», «без изменений». Во втором случае более высокая ремонтопригодность будет характеризовать конструкцию, для которой количество параметров, оцененных словом «лучше», будет больше.

Анализ надежности металлургических машин часто показывает их низкую ремонтопригодность. Так, например, для демонтажа 1 т отказавшего оборудования требуется предварительно демонтировать до 20 т исправного оборудования. Отсутствуют средства контроля и технической диагностики; низкий уровень механизации слесарно-сборочных работ; неудобные позы ремонтников; существующие сроки плановых ремонтов оборудования не являются оптимальными с точки зрения минимума затрат на восстановление работоспособности и потерь, связанных с простоем оборудования.

Существующая система технического обслуживания и ремонта (ТОиР) не отвечает условиям оптимальности. Поэтому необходимо рассматривать различные возможные стратегии восстановлений и на основе математического подхода устанавливать оптимальные сроки замены оборудования.

Глава 8. Испытание на надежность

8.1. Сбор информации

Определённый уровень надёжности машины формируется при конструировании, обеспечивается при изготовлении и реализуется в процессе применения её по назначению.

Специалист, занимающийся техническим обслуживанием металлургических агрегатов и машин, должен обеспечить их работоспособность в процессе эксплуатации.

Металлургические машины - это крупногабаритные, уникальные агрегаты, для которых в большинстве случаев невозможны контрольные испытания с целью установления фактического уровня надёжности как в целом для агрегата, так и для отдельных составных его частей.

Установить фактический уровень надёжности возможно только непосредственно в процессе эксплуатации машин, собирая информацию о техническом состоянии оборудования, о нарушениях и причинах нарушения его работоспособного состояния.

При экспериментальных оценках надёжности независимо от того, какое свойство исследуется, всё многообразие оцениваемых показателей сводится к показателям двух типов:

– показатели типа наработки - средняя или g -процентная наработка (до отказа, между отказами, до предельного состояния и т.п.);

– показатели типа вероятности (вероятность безотказной работы, вероятность восстановления за заданное время и т.д.).

При определении показателей типа наработки непосредственно наблюдаемыми величинами являются случайные интервалы: наработки до отказа, на отказ, до предельного состояния, времени восстановления и т.п. Существует 14 планов испытаний на надежность с измерением наработки.

При определении показателей типа вероятности непосредственно наблюдаемыми случайными величинами являются числа событий в испытаниях: число отказов, число предельных состояний, число восстановлений и т.д. В этом случае применяется биноминальный план испытаний.

Информация, собранная по определённым правилам и подвергнутая статистической обработке, позволяет решать задачи, связанные с эффективностью эксплуатации и модернизацией оборудования.

Накопление достаточного объёма информации необходимо для оценивания показателей надёжности с целью:

* анализа надёжности машин;

* определения необходимого количества запасных частей;

* планирования объёма ремонтных работ;

* установления оптимальных межремонтных периодов;

* планирования оптимальной периодичности диагностирования.

Выбор того или иного метода оценивания показателей надёжности определяется характером априорных сведений о функции распределения наработок до отказа.

Если вид функции распределения известен, то задача сводится к получению показателей надёжности.

Когда вид функции распределения наблюдаемой случайной величины (наработки) неизвестен или известен лишь предположительно, то процесс оценивания показателей надёжности в качестве обязательных должен включать следующие этапы:

– сбор информации об отказах оборудования;

– статистическая обработка информации;

– оценивание показателей надёжности.

Оценивание показателей надёжности (безотказности) при отсутствии информации о виде функции распределения наработок возможно при использовании так называемых непараметрических методов.

Дата добавления: 2014-12-08