Практикум по решению задач

Методические указания по выполнению контрольных работ

По дисциплине «Математика» в течение семестра проводятся две контрольные работы (одна аудиторная, одна домашняя). Темы аудиторных контрольных работ указаны в плане семинарских занятий (см. выше).

В аудиторную контрольную работу включаются задачи и тестовые задания тех типов, которые были разобраны на предшествующих практических занятиях. В домашнее задание тесты не включаются.

Для контроля усвоения теоретического материла целесообразно по усмотрению лектора проведение коллоквиума (в середине семестра) в устной или письменной форме.

Дата проведения контрольной работы, характер вопросов и типы задач объявляются студентам заранее.

Первую часть следующего за аудиторной контрольной работой занятия необходимо посвятить тщательному ее разбору с акцентом на наиболее типичных ошибках. На разбор домашнего задания, как правило, не хватает аудиторного времени. Поэтому проверенное задание следует снабдить подробной рецензией (по аналогии с курсовой работой)

Контрольные работы являются очень важной формой промежуточной аттестации обучающихся. Полученные результаты, как правило, служат хорошими сигналами для всех заинтересованных в конечном результате сторон.

В этом параграфе приведены наиболее типичные примеры решения задач по одной теме из каждого раздела.

Раздел 1

Задача. Пусть точка А(1; 3) - вершина квадрата ABCD, а его диагональ BD лежит на прямой х + 2 у - 12 = 0. Найти:

а) координаты вершин В, С и D;

b) уравнения сторон АВ, ВС, CD и AD.

Указание. Из школьного курса геометрии известны следующие свойства диагоналей квадрата, которые будут использованы при решении этой задачи.

Диагонали квадрата: 1) взаимно перпендикулярны; 2) делятся точкой своего пересечения - центром квадрата - пополам; 3) равны.

Решение: 1. Найдем уравнение прямой, на которой лежит АС - вторая диагональ квадрата. Вспомним, что уравнение любой невертикальной прямой может быть приведено к виду у = kx + b, где параметр k - угловой коэффициент этой прямой.

В силу свойства диагоналей квадрата угловые коэффициенты =-0,5 и k _BD прямых АС и BD связаны соотношением

k _AC× k _BD = -1 (1)

Найдем угловой коэффициент k _BD. Для этого выразим у через х из данного уравнения прямой BD: 2 у = - х + 12, откуда у =-0,5 х + 6. Итак, k _BD =-0,5. Поэтому из соотношения (1) получим, что k _AC=2.

Теперь уже легко найти уравнение прямой АС. Нам известны координаты ее точки А и угловой коэффициент k _AC. Используем уравнением прямой, проходящей через данную точку в данном направлении:

у - у _А = k _AC×(x - x _A)

Подставим в это уравнение числовые данные нашей задачи: x _A = 1, у _А = 3, k _AC=2. Получим у - 3 = 2(х - 1) или (после упрощений)

AC: у = 2 х + 1.

2. С помощью свойства 2) диагоналей квадрата найдем координаты центра Е квадрата - точки пересечения его диагоналей.

Поскольку точка Е лежит на диагонали АС, ее координаты удовлетворяют уравнению прямой АС; аналогично рассуждая, получим, что координаты точки Е должны одновременно удовлетворять и уравнению прямой BD. Таким образом, координаты точки Е должны удовлетворять системе из уравнений прямых АС и BD

(первое - уравнение прямой АС, второе - прямой BD).

Далее, вычитая второе уравнение из первого, получим: 0=2,5 x -5. Значит х = 2. Подставим найденное значение х в любое из уравнений системы, например, в первое. Найдем, что у = 5.

Итак, мы нашли координаты точки Е, центра квадрата: х _Е = 2, у _Е = 5, т.е. Е(2; 5).

3. Найдем длину отрезка АЕ - половину диагонали квадрата, а затем воспользуемся тем, что и остальные вершины квадрата находятся от его центра E на таком же расстоянии (свойства 2) и 3) диагоналей), т.е. что все вершины квадрата лежат на окружности радиуса АЕ с центром в точке Е

B

A

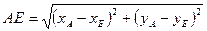
Подставив в правую часть этой формулы числовые значения координат точек А и Е, получим, что

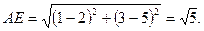
Уравнение окружности радиуса АЕ с центром в точке Е записывается в виде

(х - х_Е)² + (у - у_Е)² = (АЕ)².

Подставив в него числовые значения радиуса АЕ и координат центра Е, получим уравнение окружности, проходящей через все вершины квадрата:

(х - 2)² + (у - 5)² = 5.

Теперь с помощью простого рассуждения находим по очереди координаты всех вершин квадрата.

Точки А и С лежат на пересечении найденной окружности и прямой АС, это общие точки указанных окружности и прямой. Значит, координаты этих точек - решения системы уравнений окружности и прямой:

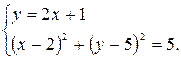
Координаты вершины А мы знаем, поэтому будем искать вершину С.

Подставим во второе уравнение системы вместо у его выражение 2 х + 1 из первого уравнения. Получим:

(х - 2)² + (2 х + 1 - 5)² = 5,

откуда (х - 2)² + (2 х - 4)² = 5, поэтому (х - 2)² + 4(х - 2)² = 5, т.е. 5(х - 2)² = 5, значит (х - 2)² = 1. Если квадрат числа равен 1, это число равно либо 1, либо (-1). Поэтому х - 2 = 1 и тогда х = 3, либо х - 2 = -1 и тогда х = 1.

Во втором случае мы получили известную нам абсциссу вершины А (а из первого уравнения системы получим ординату этой вершины), а первый случай дает нам абсциссу вершины С: х _С = 3. Тогда из первого уравнения системы найдем ординату вершины С: у _С = 2×3 + 1 = 7. Итак, найдена вершина С(3; 7).

Аналогично, для нахождения координат вершин В и D надо решить систему, состоящую из уравнений прямой BD и той же окружности:

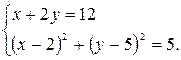
Выразим из первого уравнения х через у: х = 12 - 2 у. и подставим полученное выражение во второе уравнение системы. Получим (аналогично решению предыдущей системы) 4(у - 5)² + (у - 5)² = 5, откуда либо у - 5 = 1 и тогда у = 6, либо у - 5 = -1 и тогда у = 4.

При у = 6 первое уравнение системы дает х = 12 - 2 у = 12 - 12 = 0, а при у = 4 аналогично получаем, что х = 4.

Итак, получены два решения системы, пары (0; 6) и (4; 4). Одно из этих решений - координаты точки В, а второе - точки D. Поскольку обе эти вершины совершенно равноправны, мы можем любую из них обозначить буквой В, тогда вторая будет вершиной D. Вся разница в том, идут ли вершины А, В, С и D в порядке обхода контура квадрата по или против часовой стрелки, что для решения нашей задачи безразлично; просто надо выбрать одно из этих направлений произвольно.

Мы будем считать, что вершины квадрата таковы: B(0; 6); D(4; 4).

4. Нам осталось найти уравнения сторон квадрата. Для этого вспомним уравнение прямой, проходящей через точки М(х _М; у _М) и N(x _N; y _N):

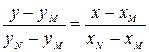(2)

и подставим в него координаты соответствующих вершин квадрата.

Уравнение прямой АВ получим, если в формуле (2) вместо точек М и N возьмем точки А и В:

.

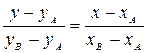Подставляя в это уравнение координаты вершин А(1; 3) и В(0; 6), находим:

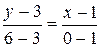или y -3=-3(x -1), откуда y =-3 x +6.

Аналогично получаем уравнения других сторон. Теперь можно сделать чертеж.

Ответ: а) В(0; 6); С(3; 7); D(4; 4);

b) AB: y = -3 x + 6;

BC: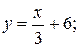

CD: y = -3 x + 16;

DA: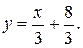

Замечание. Если иначе выбрать точки B и D (cм. п.3 решения), в ответе надо поменять местами: в п. а) - координаты точек В и D; в п. b) - уравнения прямых АВ и CD, а также уравнения прямых ВС и CD.

Раздел 2

Задача. Исследовать функцию 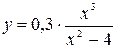и построить её график.

Решение:

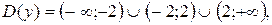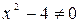1).Область определения функции т.к. при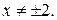

2).Исследуем функцию на четность

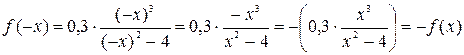
Функция нечетная, значит её график симметричен относительно начала координат.

3) Точки пересечения с осями. Если x =0, y =0.Следовательно, cуществует единственная точка пересечения с осями О(0;0).

4) Функция является непрерывной в своей области определения, а в точках -2 и 2, не принадлежащих D (y), имеет разрывы 2-го рода.

5).Найдем уравнения асимптот:

Вертикальные асимптоты. х= -2 и х= 2т.к.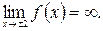

Наклонные асимптоты. 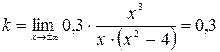и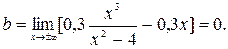

Таким образом уравнение наклонной асимптоты имеет вид: у =0,3 х.

6).Определим интервалы возрастания и убывания функции, а также критические точки. Для этого найдём первую производную нашей функции (достаточно найти только числитель, т.к. знаменатель всегда больше нуля). Числитель производной имеет вид: .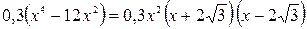

Отсюда видно, что на интервалах 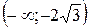и 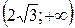производная положительна, а значит исходная функция возрастает, а на интервалах 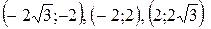производная отрицательна и поэтому на этих промежутках функция убывает.

Точки 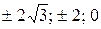являются критическими. При переходе через точку 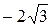прозводная меняет знак с минуса на плюс и поэтому в этой точке функция имеет

локальный максимум равный 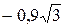. При переходе через точку 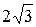произзводная меняет знак с плюса на минус и поэтому в этой точке функция имеет локальный минимум равный 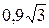. При переходе через точку 0 производная знак не меняет, и поэтому в этой точке локального экстремума нет. В точках же -2 и 2 функция не определена.

7). Найдём интервалы, на которых график функции является выпуклым вверх или вниз.

Вторая производная функции имеет вид: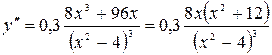

На интервалах 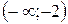и 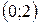вторая производная меньше нуля, поэтому график функции является выпуклым вниз. На интервалах 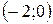и (2; ¥) вторая производная больше нуля, поэтому график функции является выпуклым вверх. В точке 0 вторая производная меняет знак, следовательно, в этой точке график функции имеет перегиб.

Используя проведённое исследование, можно построить график функции.

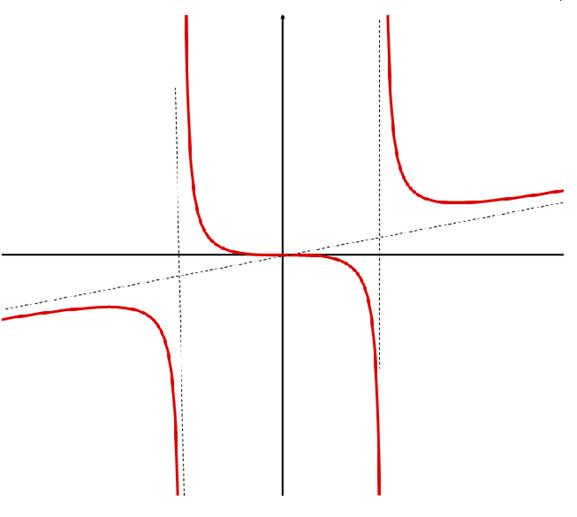
Раздел 3

Задача. Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в них равно 20, 15 и 10 соответственно. Из произвольной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращается в свою партию, и оттуда вторично берется деталь, которая также оказывается стандартной. Найти вероятность того, что детали извлекались из третьей партии.

Решение:

Эта задача на применение формулы Байеса. Мы не знаем из какой партии извлечена деталь. Поэтому выдвигаем гипотезы: Н₁ ={деталь извлечена из первой партии}, Н₂ ={деталь извлечена из второй партии}, Н₃ ={деталь извлечена из третьей партии}. Поскольку все партии равноправны, то Р (Н ₁)= Р (Н ₂)= Р (Н ₃)=1/3. Условные вероятности вытаскивания (с возвращением) двух стандартных деталей из соответствующих партий равны

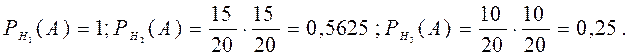
Подставляя эти значения в формулу Байеса, получаем

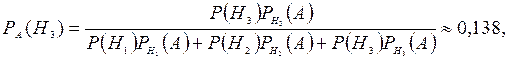
что в 2,5 раза меньше первоначальной вероятности третьей гипотезы. Это следствие того, что в третьей партии только половина деталей стандартна.

Дата добавления: 2014-12-08