Вещество в электрическом поле(или электрическое поле в веществе)

Теорема Остроградского-Гаусса для поля распределенных зарядов; ее применение для определения параметров поля бесконечного линейного заряда.

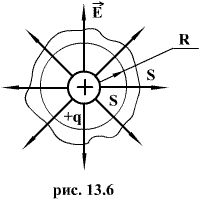
Определим поток напряжённости поля электрических зарядов через некоторую замкнутую поверхность, окружающую эти заряды. Рассмотрим сначала случай сферической поверхности радиуса R, окружающей один заряд, находящийся в ее центре (рис. 13.6). Напряженность поля по всей сфере одинакова и равна .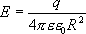

Силовые линии направлены по радиусам, т.е. перпендикулярны поверхности сферы S_n, следовательно 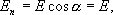т.к. 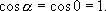Тогда поток напряженности будет равен 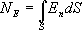. Используя формулу напряжённости, находим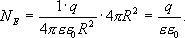

Окружим теперь сферу произвольной замкнутой поверхностью S’. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно формула справедлива не только для сферы, но и для любой замкнутой поверхности. Если произвольной поверхностью окружаем n зарядов, то очевидно, что поток напряженности через эту поверхность равен сумме потоков, создаваемых каждым из зарядов, т.е. 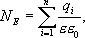, или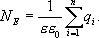

Таким образом, полный поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы численно равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности, поделенной на. Это положение называется теоремой Остроградского - Гаусса. С помощью этой теоремы можно определить напряженность полей, создаваемых заряженными телами различной формы.

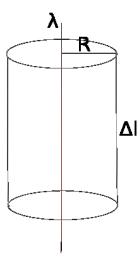
Расчёт напряжённости поля бесконечной нити.

Рассмотрим поле, создаваемое бесконечной прямолинейной нитью с линейной плотностью заряда, равной λ. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии R от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом R и высотой Δl. Тогда поток напряжённости через эту поверхность по теореме Гаусса таков (в единицах СИ): 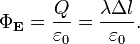В силу симметрии вектор напряженности поля направлен перпендикулярно нити, прямо от нее (или прямо к ней); модуль этого вектора в любой точке поверхности цилиндра одинаков. Тогда поток напряжённости через эту поверхность можно рассчитать следующим образом: 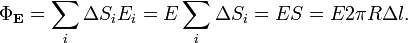Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю (вследствие направления E по касательной к ним). Приравнивая два полученных выражения для 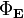, имеем: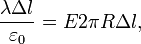

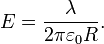
Проводники и диэлектрики. По электрическимсв-вам тела можно разделить на проводники и диэлектрики. Проводниками наз-т тела, через кот-е электрические заряды могут переходить от заряж-го тела к незаряж-ному. Способность проводников пропускать через себя электрические заряды объясняется наличием в них свободных носителей заряда. Примерами проводников могут служить металлические тела в твердом и жидком сост-ии, жидкие растворы электролитов. Диэлектриками или изоляторами наз-тся такие тела, через кот-е эл-кие заряды не могут переходить от заряж-го тела к незаряж-му. К диэлектрикам, например, относятся воздух и стекло, плексиглас и эбонит, сухое дерево и бумага.

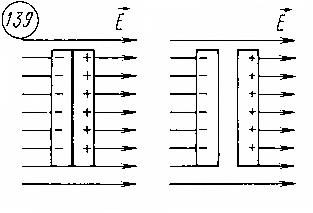
Проводники в электрическом поле.

Явление разделения разноименных зарядов в проводнике, помещенном в эл/поле, наз-ся электростатической индукцией. При внесении в эл/поле тела из проводника свободные заряды в нем приходят в движение. Перераспределение зарядов вызывает изменение эл/поля. Дв-ие зарядов прекращается только тогда, когда напряженность эл/поля в проводнике становится равной нулю. Свободные заряды перестают перемещаться вдоль пов-ти проводящего тела при достижении такого распределения, прикот-м вектор напряженности эл/поля в любой точке перпендикулярен пов-ти тела. Поэтому в эл/поле пов-ть проводящего тела любой формы явл-ся эквипотенциальной поверхностью.

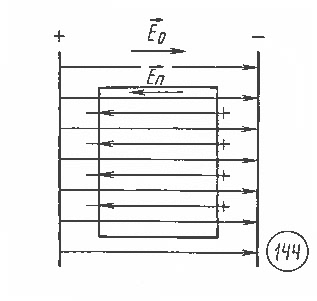
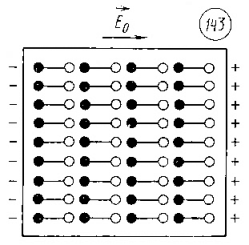
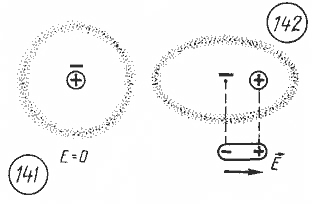Диэлектрики в электрическом поле. При отсутствии эл/поля электронное облако расположено симметрично отн-но атомного ядра (рис. 141), а в эл/поле с напряженностью оно изменяет свою форму и центр отрицательно заряженного электронного облака уже не совпадает с центром положительного атомного ядра (рис. 142). В рез-те поляризации на пов-ти вещества появл-ся связанные заряды (рис. 143). Эти заряды обусловливают взаимодействие нейтральных тел из диэлектрика с заряженными телами. Вектор напряженности эл/поля, создаваемого связанными зарядами на пов-ти диэлектрика, направлен внутри диэлектрика противоположно вектору напряженности внешнего эл/поля, вызывающего поляризацию (рис. 144).

Напряженность эл/поля внутри диэлектрика оказывается равной 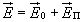. Физическая величина, равная отношению модуля напряженности эл/поля в вакууме к модулю напряженности эл/поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества: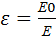

4. Электроемкость тел. Электроемкость системы конденсаторов.

Сообщенный проводнику заряд распределяется по его поверхности так, чтобы напряженность поля внутри проводника была равна нулю.При этом проводник приобретает некоторый потенциал ϕ. Если проводнику сообщить дополнит-й заряд, то он также перераспределится по его пов-ти, и потенциал проводника изменится.Опыт показывает, что потенциал проводника пропорционален находящемуся на нем заряду 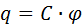. где коэф-т пропорциональности С назван электроемкостью.Сообщение телу заряда возможно перемещением электронов (или других заряженных частиц) на это тело от другого под действием электрической силы.При этом другое тело приобретает такой же по величине заряд (некомпенсированный),что и первое тело,но противоположного знака. Т.о. электроемкость (емкость) создается всегда двумя телами (проводниками).Такая c/c н-сяконденсатором.Электроемкость конденсатора равна 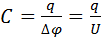. где q – заряд конденсатора (одного из его образующих тел), ∆ϕ – разность потенциалов между телами, U – напр-е на конденсаторе. Электроемкость конденсатора, образованного двумя плоскими пластинами с площадью S и расстоянием между ними d равна 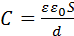, где ε – относительная диэлектрическая проницаемость среды между пластинами (обкладками конденсатора).

Соединение конденсаторов, их эквивалентная емкость. 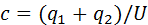или

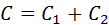
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При парал-м соед-и конденсаторов напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = С2U. Такую с/с можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2 при напряжении между обкладками равном U. Отсюда следует. При послед-м соединении одинаковыми оказываются заряды обоих конденсаторов: q1 = q2 = q, а напряжения на них равны и Такую с/с можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U1 + U2. Следовательно,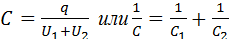

Дата добавления: 2014-12-08