Электронная теория электропроводности. Электропроводность полупров-ков

Энергия и плотность энергии электрического поля.

Формулу энергии поля конденсатора можно также получить, осуществив мысленный эксперимент по перемещению обкладки плоского конденсатора в однородном поле другой обкладки E1 на расстояние d:

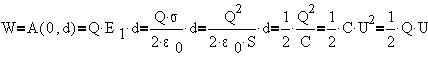
Интересно провести преобразования так, чтобы в формуле фигурировали напряженность поля конденсатора Е=2E1 и его геометрические размеры:

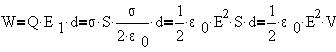
Полученная формула показывает, что энергия электрического поля рассредоточена по всему объему, занимаемому полем, с плотностью энергии, равной:

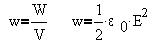
Здесь видно, что w численно равна энергии единицы объема поля. При наличии в области поля диэлектрика плотность энергии и полная энергия поля возрастают в раз (дополнительный заряд для компенсации поля поверхностного заряда диэлектрика):

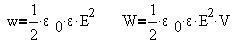
Исходя из представлений о свободных электронах, Друде разработал классическую теорию электропроводности металлов, которая затем была усовершенствована Лоренцем. Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершено свободно, пробегая в среднем некоторый путь. Правда в отличие от молекул газа, пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, оценку средней скорости теплового движения электронов можно произвести по формуле

.

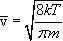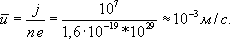Для комнатной температуры (300К) вычисление по этой формуле приводит к следующему значению: 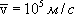. При включении поля на хаотическое тепловое движение, происходящее, со скоростью , накладывается упорядоченное движение электронов с некоторой средней скоростью 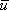. Величину этой скорости легко оценить, исходя из формулы, связывающей плотность тока j с числом n носителей в единице объема, их зарядом е и средней скоростью 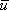: 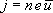Предельная допустимая техническими нормами плотность тока для медных проводов составляет около 10 А/мм2 = 107 А/м2. Взяв для n=1029 м-3, получим

Таким образом, даже при больших плотностях тока средняя скорость упорядоченного движения зарядов в 10⁸раз меньше средней скорости теплового движения.

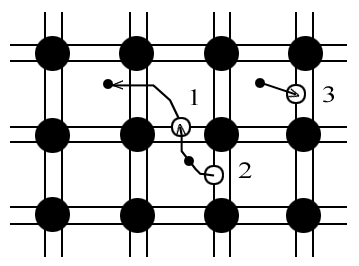Электропроводность полупроводников. Полупроводники – вещества, в которых в валентной зоне находится 4 электрона. (Кремний). При температуре Т=0 К все связи заполнены электронами, что соответствует полностью заполненной валентной зоне и пустой зоне проводимости, отделенной от валентной зоны по энергии на 1,1 эВ. При увеличении температуры до примерно 200-300 К некоторые электроны из валентной зоны смогут перейти в зону проводимости; это соответствует "уходу" электрона из ковалентной связи 1 и превращению его в "свободно перемещающийся" по кристаллу электрон. На месте опустевшей ковалентной связи образуется дырка - "разорвавшаяся" ковалентная связь, которую покинул электрон. Электрон из соседней связи может "перескочить" в "дырку", тогда дырка как бы переместится на новое место 2. Поскольку электроны и дырки образуются парами, то, очевидно, что число дырок в рассмотренном случае равно числу электронов. Один из свободных электронов может занять одну из дырок; в результате они оба исчезнут, такой процесс называется рекомбинацией электрона и дырки (3. В состоянии равновесия устанавливается равенство чисел скорости зарождения и рекомбинации электронов и дырок и связанные с ними концентрации последних, зависящие от температуры полупроводника, а также от частоты и интенсивности падающих на полупроводник излучений. Можно получить зависимость проводимости полупроводника от температуры. Вероятность образования пары электрон - дырка с минимальной энергией (очевидно, такая пара получается если электрон проводимости обладает наименьшей энергией, а дырка - наибольшей будет максимальной. Именно такие пары в основном образуются при температуре порядка и дают основной вклад в концентрацию свободных носителей заряда.

Дата добавления: 2014-12-08