Электронная природа электромагнитной индукции. Индукционный ток.

Магнитное поле движущихся зарядов (эквивалентных токов).

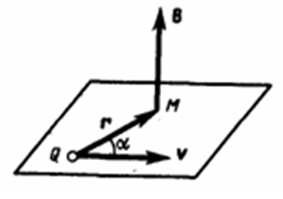Любой проводник с током создает в окруж-м простр-вемагн-е поле. При этом электрический же ток является упорядоченным дви-ем электрических зарядов. Значит можно считать, что любой движ-ся в вакууме или среде заряд порождает вокруг себя магн-е поле. В рез-те обобщения многочисленных опытных данных был установлен закон, который определяет поле В точечного заряда Q, движ-ся с постоянной скоростью v. Этот закон задается формулой 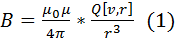где r — радиус-вектор, кот-й проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпенд-но пл-ти, в кот-й нах-ся векторы v и r: его напр-е совпадает с напр-ем поступат-годв-я правого винта при его вращении от v к r. Модуль вектора магнитной индукции (1) находится по формуле 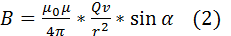где α — угол между векторами v и r. Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магн-м св-вам эквивалентен элементу тока: 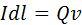Приведенные законы (1) и (2) выполняются лишь при малых скоростях (v<<с) движущихся зарядов, когда электрическое поле дви-гося с постоянной скорость заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, который находится в той точке, где в данный момент времени находится движущийся заряд. Формула (1) задает магнитную индукцию положит-го заряда, дв-гося со скоростью v. При дв-и отрицательного заряда Q заменяется на -Q. Скорость v - относительная скорость, т. е. скорость относительно системы отсчета наблюдателя. Вектор Вв данной системе отсчета зависит как от времени, так и от расположения наблюдателя. Поэтому следует отметить отн-ныйхар-р магн-го поля дв-гося заряда.

, , , ,

,

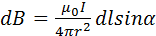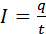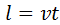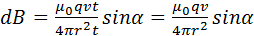Рассмотрим физические причины возникновения ЭДС индукции, а следовательно, и индукционного тока. Пусть элемент проводника длиной l движется в магнитном поле со скоростью υ. Магнитное поле однородно, вектор магнитной индукции направлен перпендикулярно плоскости от нас. На каждый свободный электрон проводника e со стороны магнитного поля действует сила Лоренца. Заряд электрона отрицательный, поэтому сила Лоренца F_Л направлена вниз. Следовательно, электроны смещаются в нижнюю часть элемента l, а вверху остается некомпенсированный положительный заряд, и на концах элемента проводника l образуется разность потенциалов ∆ϕ. Эту разность 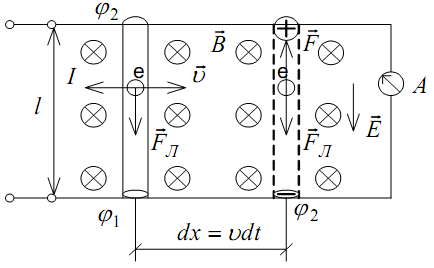потенциалов можно рассматривать как электродвижущую силу для замкнутой цепи, элементом которой является движущийся проводник. При этом в цепи устанавливается некоторый ток I. Если скорость движения проводника постоянна, то ток будет постоянным. Как следует из законов постоянного тока, разность потенциалов ∆ϕ стремится к максимально возможной величине (ε_инд), когда сопротивление внешней для движущегося проводника l цепи стремится к бесконечности (разрыв цепи). Для этого случая (как и при рассмотрении эффекта Холла) можно записать eE = − υeB или E=− υB. ε_инд =−υBl.

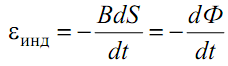
где Ф – поток магнитной индукции сцепленный с контуром. Используя закон Ома для полной цепи и закон Фарадея, выражение для индукционного тока можно записать в виде 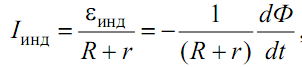где r – сопротивление проводника l; R – сопротивление внешней цепи

Дата добавления: 2014-12-08