
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекции по теме 4: Обработка результатов экспериментов 1 страница
|
|
|
|
План лекции:
1. Понятие о выборочном наблюдении, его задачи.
2. Оценки параметров генеральной совокупности по ее выборке.
3. Распространение выборочных результатов на генеральную совокупность.
4. Корреляционный и регрессионный анализ.
5. Линейная корреляция.
6. Регрессия.
7. Дисперсионный анализ.
8. Табличный процессор MS Excel.
9. Графики, диаграммы.
10. Описательная статистика и обработка экспериментальных данных.
Понятие о выборочном наблюдении, его задачи
Выборочное наблюдение – одно из наиболее современных видов статистического наблюдения. Выборочное наблюдение – это такое наблюдение, при котором обследованию подвергается часть единиц изучаемой совокупности, отобранных на основе научно разработанных принципов, обеспечивающих получение достаточного количества достоверных данных, для того чтобы охарактеризовать всю совокупность в целом.
Средние и относительные показатели, полученные на основе выборочных данных, должны достаточно полно воспроизводить или репрезентатировать соответствующие показатели совокупности в целом.
Логика выборочного наблюдения: определение объекта и целей выборочного наблюдения; выбор схема отбора единиц для наблюдения; расчет объема выборки; проведение случайного отбора установленного числа единиц из генеральной совокупности; наблюдение отобранных единиц по установленной программе; расчет выборочных характеристик в соответствии с программой выборочного определение ошибки, ее размера; распространение выборочных данных на генеральную совокупность; анализ полученных данных.
Выборочное наблюдение можно осуществить по более широкой программе.
Выборочное наблюдение более дешевое с точки зрения затрат на его проведение.
Выборочное наблюдение можно организовать тогда и в тех случаях, когда отчетностью мы воспользоваться не можем.
Полученные данные всегда содержат в себе ошибку, о результатах наблюдения можно судить лишь с определенной степенью достоверности. Но по сравнению с другими видами наблюдения это достоинство выборочного метода.
Вся совокупность единиц, из которых производится отбор, называется генеральной. Совокупность единиц отобранных называется выборочной.
Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.
Оценки параметров генеральной совокупности по ее выборке
В основе статистических выводов проведенного исследования лежит распределение случайной величины  , наблюдаемые же значения (
, наблюдаемые же значения ( ) называются реализациями случайной величины
) называются реализациями случайной величины  (
( – объем выборки). Распределение случайной величины
– объем выборки). Распределение случайной величины  в генеральной совокупности носит теоретический, идеальный характер, а ее выборочный аналог является эмпирическим распределением. Некоторые теоретические распределения заданы аналитически, т.е. их параметры определяют значение функции распределения
в генеральной совокупности носит теоретический, идеальный характер, а ее выборочный аналог является эмпирическим распределением. Некоторые теоретические распределения заданы аналитически, т.е. их параметры определяют значение функции распределения  в каждой точке пространства возможных значений случайной величины
в каждой точке пространства возможных значений случайной величины  . Для выборки же функцию распределения определить трудно, а иногда невозможно, поэтому параметры оценивают по эмпирическим данным, а затем их подставляют в аналитическое выражение, описывающее теоретическое распределение. При этом предположение (или гипотеза) о виде распределения может быть как статистически верным, так и ошибочным. Но в любом случае восстановленное по выборке эмпирическое распределение лишь грубо характеризует истинное. Важнейшими параметрами распределений являются математическое ожидание
. Для выборки же функцию распределения определить трудно, а иногда невозможно, поэтому параметры оценивают по эмпирическим данным, а затем их подставляют в аналитическое выражение, описывающее теоретическое распределение. При этом предположение (или гипотеза) о виде распределения может быть как статистически верным, так и ошибочным. Но в любом случае восстановленное по выборке эмпирическое распределение лишь грубо характеризует истинное. Важнейшими параметрами распределений являются математическое ожидание  и дисперсия
и дисперсия 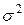 .
.
По своей природе распределения бывают непрерывными и дискретными. Наиболее известным непрерывным распределением является нормальное. Выборочными аналогами параметров  и
и 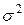 для него являются: среднее значение
для него являются: среднее значение  и эмпирическая дисперсия
и эмпирическая дисперсия  . Среди дискретных распределений в социально-экономических исследованиях наиболее часто применяется альтернативное (дихотомическое) распределение. Параметр математического ожидания
. Среди дискретных распределений в социально-экономических исследованиях наиболее часто применяется альтернативное (дихотомическое) распределение. Параметр математического ожидания  этого распределения выражает относительную величину (или долю) единиц совокупности, которые обладают изучаемым признаком
этого распределения выражает относительную величину (или долю) единиц совокупности, которые обладают изучаемым признаком  (она обозначена буквой
(она обозначена буквой  ); доля совокупности, не обладающая этим признаком, обозначается буквой
); доля совокупности, не обладающая этим признаком, обозначается буквой 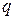 (
( ). Дисперсия же
). Дисперсия же 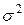 альтернативного распределения также имеет эмпирический аналог
альтернативного распределения также имеет эмпирический аналог 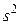 .
.
В зависимости от вида распределения и от способа отбора единиц совокупности по-разному вычисляются характеристики параметров распределения.
Долей выборки  называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:
называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности: 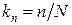 .
.
Выборочная доля  – это отношение единиц, обладающих изучаемым признаком x к объему выборки
– это отношение единиц, обладающих изучаемым признаком x к объему выборки  :
: 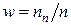 .
.
Распространение выборочных результатов на генеральную совокупность
Конечной целью выборочного наблюдения является характеристика генеральной совокупности. При малых объемах выборки эмпирические оценки параметров ( и
и  ) могут существенно отклоняться от их истинных значений (
) могут существенно отклоняться от их истинных значений ( и
и  ). Поэтому возникает необходимость установить границы, в пределах которых для выборочных значений параметров (
). Поэтому возникает необходимость установить границы, в пределах которых для выборочных значений параметров ( и
и  ) лежат истинные значения (
) лежат истинные значения ( и
и  ).
).
Доверительным интервалом какого-либо параметра 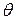 генеральной совокупности называется случайная область значений этого параметра, которая с вероятностью близкой к 1 (надежностью) содержит истинное значение этого параметра.
генеральной совокупности называется случайная область значений этого параметра, которая с вероятностью близкой к 1 (надежностью) содержит истинное значение этого параметра.
Предельная ошибка выборки  позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы, которые равны:
позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы, которые равны:
для средней 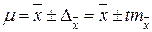
для доли 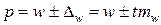 .
.
Нижняя граница доверительного интервала получена путем вычитания предельной ошибки из выборочного среднего (доли), а верхняя — путем ее добавления.
Доверительный интервал для средней использует предельную ошибку выборки и для заданного уровня достоверности p определяется по формуле:
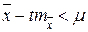 – истинное значение средней
– истинное значение средней 
 для относительного параметра (доли)
для относительного параметра (доли)
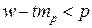 – истинное значение доли
– истинное значение доли 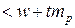
Это означает, что с заданной вероятностью  , которая называется доверительным уровнем и однозначно определяется значением
, которая называется доверительным уровнем и однозначно определяется значением 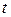 , можно утверждать, что истинное значение средней лежит в пределах от
, можно утверждать, что истинное значение средней лежит в пределах от  до
до  , а истинное значение доли
, а истинное значение доли  – в пределах от
– в пределах от  до
до 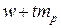 . При расчете доверительного интервала для трех стандартных доверительных уровней
. При расчете доверительного интервала для трех стандартных доверительных уровней  ,
, 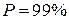 и
и  значение
значение 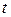 выбирается по таблице Стьюдента. Приложения в зависимости от числа степеней свободы
выбирается по таблице Стьюдента. Приложения в зависимости от числа степеней свободы 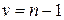 . Если объем выборки достаточно велик, то соответствующие этим вероятностям значения
. Если объем выборки достаточно велик, то соответствующие этим вероятностям значения 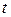 равны: 1,96, 2,58 и 3,29. Таким образом, предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы.
равны: 1,96, 2,58 и 3,29. Таким образом, предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы.
Распространение результатов выборочного наблюдения на генеральную совокупность в социально-экономических исследованиях имеет свои особенности, так как требует полноты представительности всех ее типов и групп. Основой для возможности такого распространения является расчет относительной ошибки:
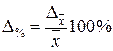 – для средней
– для средней
 – для доли
– для доли
где  – относительная предельная ошибка выборки
– относительная предельная ошибка выборки 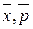 .
.
Существуют два основных метода распространения выборочного наблюдения на генеральную совокупность: прямой пересчет и способ коэффициентов.
Сущность прямого пересчетазаключается в умножении выборочного среднего значения на объем генеральной совокупности N.
Способ коэффициентов целесообразно использовать в случае, когда выборочное наблюдение проводится с целью уточнения данных сплошного наблюдения.
При этом используют формулу:

где все переменные – это численность совокупности:
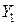 – с поправкой на недоучет,
– с поправкой на недоучет, 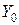 – без этой поправки,
– без этой поправки,  – в контрольных точках,
– в контрольных точках,  – в тех же точках по данным контрольных мероприятий.
– в тех же точках по данным контрольных мероприятий.
Корреляционный и регрессионный анализ
Существующие между явлениями формы и виды связей весьма разнообразны по своей классификации. Предметом статистики являются только такие из них, которые имеют количественный характер и изучаются с помощью количественных методов. Рассмотрим метод корреляционно-регрессионного анализа, который является основным в изучении взаимосвязей явлений.
Данный метод содержит две свои составляющие части – корреляционный анализ и регрессионный анализ. Корреляционный анализ – это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ – это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами.
Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая – от 0,1 до 0,3; умеренная – от 0,3 до 0,5; заметная – от 0,5 до 0,7; высокая – от 0,7 до 0,9; весьма высокая (сильная) – от 0,9 до 1,0. Она используется далее в примерах по теме.
Между любыми двумя, тремя… случайными величинами возможно существование следующих вариантов зависимостей:
1. отсутствие какой-либо зависимости;
2. статистическая зависимость – это зависимость между случайными величинами, когда изменение одной величины вызывает изменение параметров распределения или вида самого распределения другой случайной величины;
3. функциональная зависимость – это зависимость между случайными величинами, которая может быть описана в виде функции  .
.
Установить зависимость между случайными величинами можно либо графически, но это возможно только в случае двух-трех случайных величин, либо с помощью корреляционного анализа. Корреляционный анализ позволяет не только установить наличие зависимости между случайными величинами, но и дать качественную характеристику этой связи. В качестве такой меры служит коэффициент корреляции. Различают следующие виды коэффициентов корреляции:
1. парный линейный выборочный коэффициент корреляции 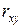 ;
;
2. корреляционное отношение  ;
;
3. множественный коэффициент корреляции  и частный выборочный коэффициент корреляции
и частный выборочный коэффициент корреляции 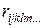 ;
;
4. ранговые коэффициенты корреляции Спирмена и Кендалла.
Особая ценность корреляционного анализа заключается в способности оценить наличие зависимости между влияющими на параметр оптимизации факторами, чтобы проверить выполнимость требования не коррелированности совокупности факторов. Существует следующее правило: если сила связи между двумя факторами не превышает умеренную, то можно оба фактора оставить в рассмотрении. В противном случае – один из двух факторов из рассмотрения выбрасывается. Конечно, это правило можно смягчить, разрешив использование факторов, между которыми наблюдается заметная связь, но, как правило, это делать не рекомендуется.
При оценивании связи между факторами существует одна опасность.
Дело в том, что корреляционный анализ, как и любой другой математический аппарат работает, прежде всего, с цифрами, не обращая внимания на природу их возникновения и физический смысл. Поэтому в ходе проверки может возникнуть наличие высокой и более связи между теми случайными величинами, где ее не может вообще существовать по логике вещей. Конечно, для устранения подобных случаев существует проверка значимости коэффициента корреляции, но голову экспериментатора тоже не следует исключать из анализа. В моей практике был случай, когда студент утверждал, что качество сгущенного молока напрямую зависит от того, в банку какого цвета оно упаковано – синюю или зеленую. Свое утверждение он аргументировал тем, что между этими характеристиками существует весьма высокая корреляционная зависимость. Чтобы Вам не попасться на подобную удочку, будьте внимательны!
А теперь рассмотрим все указанные выше виды коэффициентов корреляции. При этом будем приводить только используемые на практике формулы расчета коэффициентов корреляции и оценки их значимости. Теоретические выводы данных формул, при желании, можно найти в учебной и учебно-методической литературе по теории вероятностей и математической статистике.
Линейная корреляция
Парный выборочный линейный коэффициент корреляции предназначен для выявления линейной связи между двумя случайными величинами. Определяется по экспериментальной выборке значений случайных величин  и
и 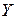 . Отсюда и название данного коэффициента. Следует понимать, что равенство нулю данного коэффициента корреляции говорит об отсутствии линейной зависимости между
. Отсюда и название данного коэффициента. Следует понимать, что равенство нулю данного коэффициента корреляции говорит об отсутствии линейной зависимости между  и
и 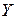 , т.е. зависимости типа
, т.е. зависимости типа  , во всех ее возможных проявлениях. Отсутствие вообще какой-либо зависимости между случайными величинами (нелинейной или статистической) может подтвердить только корреляционное отношение, которое будет рассмотрено ниже.
, во всех ее возможных проявлениях. Отсутствие вообще какой-либо зависимости между случайными величинами (нелинейной или статистической) может подтвердить только корреляционное отношение, которое будет рассмотрено ниже.
Парный выборочный линейный коэффициент корреляции на практике удобнее всего определять по формуле:
 .
.
Отметим свойства парного линейного выборочного коэффициента корреляции.
1.  . Причем:
. Причем:
a.  – наличие линейной связи между случайными величинами
– наличие линейной связи между случайными величинами  и
и 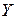 ,
,
b.  – отсутствие линейной связи между случайными величинами
– отсутствие линейной связи между случайными величинами  и
и 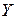 ,
,
c.  – наличие либо нелинейной, либо статистической связи между случайными величинами
– наличие либо нелинейной, либо статистической связи между случайными величинами  и
и 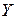 .
.
2.  – между случайными величинами
– между случайными величинами  и
и 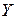 наблюдается обратная зависимость, т.е. при возрастании значений одной случайной величины значения другой случайной величины уменьшаются,
наблюдается обратная зависимость, т.е. при возрастании значений одной случайной величины значения другой случайной величины уменьшаются,
3.  – между случайными величинами
– между случайными величинами  и
и 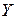 наблюдается прямая зависимость, т.е. при возрастании значений одной случайной величины значения другой случайной величины также увеличиваются,
наблюдается прямая зависимость, т.е. при возрастании значений одной случайной величины значения другой случайной величины также увеличиваются,
4.  .
.
5. При увеличении (уменьшении) значений случайных величин на одно и то же число (или в одно и то же число раз) значение 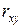 остается неизменным.
остается неизменным.
6. 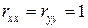 – поскольку это действие случайной величины самой на себя.
– поскольку это действие случайной величины самой на себя.
Внимание на свойство 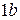 . Если
. Если  , то мы говорим об отсутствии только линейной зависимости. Говорить об отсутствии зависимости между случайными величинами
, то мы говорим об отсутствии только линейной зависимости. Говорить об отсутствии зависимости между случайными величинами  и
и 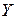 вообще можно после проверки корреляционного отношения.
вообще можно после проверки корреляционного отношения.
Значимость 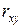 проверяется по критерию согласия Стьюдента. При этом в качестве основной гипотезы проверяется гипотеза об отсутствии линейной корреляции, т.е.
проверяется по критерию согласия Стьюдента. При этом в качестве основной гипотезы проверяется гипотеза об отсутствии линейной корреляции, т.е.  :
:  и
и 
 .
.
Наблюдаемое значение критерия определяется по формуле:
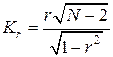 , где
, где 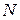 – общее число опытов.
– общее число опытов.
Парный выборочный линейный коэффициент корреляции признается значимым (т.е. основная гипотеза отвергается), если 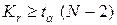 .
.
Регрессия
Регрессионный анализ представляет собой математический аппарат, который служит для построения математической модели эксперимента. Как уже упоминалось в параграфе 1.4, в планировании эксперимента чаще всего выбираются математические модели полиномиального характера.
Там же отмечалось, что экспериментатора после отбора полиномиальной модели заботит поиск ее коэффициентов. Фактически, этой фразой была определена задача регрессионного анализа с математической точки зрения.
Поясним эту мысль на примере.
Простейшая полиномиальная модель имеет вид:
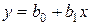 .
.
Из предварительно проведенных опытов экспериментатору известны значения фактора  и результаты эксперимента
и результаты эксперимента  , которые при этих значениях фактора были зарегистрированы. Глядя на уравнение, сразу становится видно, что единственное, что неизвестно экспериментатору – коэффициенты
, которые при этих значениях фактора были зарегистрированы. Глядя на уравнение, сразу становится видно, что единственное, что неизвестно экспериментатору – коэффициенты  и
и  . Таким образом, с математической точки зрения регрессионный анализ сводится к поиску неизвестных коэффициентов
. Таким образом, с математической точки зрения регрессионный анализ сводится к поиску неизвестных коэффициентов  и
и  этой модели.
этой модели.
Для определения коэффициентов полиномиальных моделей используются, чаще всего, метод моментов и метод наименьших квадратов. Причем, второй метод является самым популярным. Более того, в большинстве программных статистических пакетов для поиска коэффициентов уравнений используется именно метод наименьших квадратов.
Рассматривать данный метод будем на примере уравнения, приведенного выше.
Пусть была проведена серия из 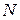 опытов, при этом в каждом из проведенных опытов зависимость между установленным значением фактора
опытов, при этом в каждом из проведенных опытов зависимость между установленным значением фактора  и полученным значением функции отклика
и полученным значением функции отклика  определялась выражением:
определялась выражением:
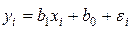 ,
,
где  – отклонение вследствие каких-либо случайных причин (погрешности).
– отклонение вследствие каких-либо случайных причин (погрешности).
После проведения всей серии опытов общая модель будет описываться совокупностью значений  на отдельных этапах, т.е.
на отдельных этапах, т.е.
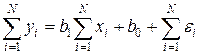 .
.
При построении модели эксперимента исследователь, вполне естественно, старается свести к минимуму отклонения отдельных экспериментов, т.е. можно записать:
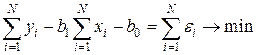 .
.
Фактически, необходимо решить задачу по поиску минимума приведенной выше функции. Но прежде, чем заняться данной проблемой, нужно учесть еще один момент. Отклонения  могут быть как положительные, так и отрицательные. В результате простого суммирования
могут быть как положительные, так и отрицательные. В результате простого суммирования  может возникнуть эффект компенсации: результат окажется либо ниже, чем есть на самом деле, либо вообще равным нулю. Чтобы избежать этого, обычно суммируют не сами отклонения, а их квадраты. Тогда получим, что в результате всех этих математических операций задача сводится к задаче поиска минимума функции
может возникнуть эффект компенсации: результат окажется либо ниже, чем есть на самом деле, либо вообще равным нулю. Чтобы избежать этого, обычно суммируют не сами отклонения, а их квадраты. Тогда получим, что в результате всех этих математических операций задача сводится к задаче поиска минимума функции  при неизвестных коэффициентах
при неизвестных коэффициентах  и
и  .
.
Для их нахождения нужно решить систему нормальных уравнений:

Сначала необходимо провести проверку значимости уравнения регрессии, поскольку, если уравнение не значимо, то оценивать значимость коэффициентов не имеет смысла. Вторым шагом проводиться проверка значимости коэффициентов уравнения регрессии.
1) Оценка значимости уравнения регрессии.
Оценка значимости уравнения проводится по методике дисперсионного анализа. Проверить значимость уравнения регрессии – значит установить, является ли установленное из априорной информации уравнение регрессии адекватной моделью для исследуемого процесса (явления) и достаточно ли переменных для описания данного процесса было использовано.
В отличие от классического дисперсионного анализа, при оценке значимости уравнения регрессии рассматриваются следующие группировки данных: общая, регрессия и остаточная. Для оценки значимости коэффициента регрессии необходимо оценить:
1. Среднее значение параметра оптимизации  во всей серии опытов:
во всей серии опытов:

где 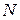 – общее число опытов.
– общее число опытов.
2. Значения параметра оптимизации 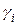 , рассчитанные по определенному ранее уравнению регрессии.
, рассчитанные по определенному ранее уравнению регрессии.
Дисперсионный анализ
В общем случае, задачей дисперсионного анализа является выявление тех факторов, которые оказывают существенное влияние на результат эксперимента. Помимо этого. Дисперсионный анализ может применяться для сравнения средних нескольких выборок, если число выборок больше двух.
Для этой цели служит однофакторный дисперсионный анализ. В целях решения поставленных задач принимается следующее. Если дисперсии полученных значений параметра оптимизации в случае влияния факторов отличаются от дисперсий результатов в случае отсутствия влияния факторов, то такой фактор признается значимым.
Как видно из формулировки задачи, здесь используются методы проверки статистических гипотез, а именно – задача проверки двух эмпирических дисперсий. Следовательно, дисперсионный анализ базируется на проверке дисперсий по критерию Фишера.
В зависимости от того, сколько факторов принимается в рассмотрение, различают однофакторный (случай простой группировки) и многофакторный дисперсионный анализ. Частным случаем второго является двухфакторный дисперсионный анализ (случай двойной группировки).
В рамках этих двух случаев различают следующие виды дисперсионного анализа:
• однофакторный дисперсионный анализ с одинаковым числом испытаний по уровням фактора;
• однофакторный дисперсионный анализ с неодинаковым числом испытаний по уровням фактора;
• двухфакторный дисперсионный анализ без повторений;
• двухфакторный дисперсионный анализ с повторениями.
Рассмотрим однофакторный дисперсионный анализ с одинаковым числом испытаний на уровнях фактора.
|
|
|
|
|
Дата добавления: 2014-12-10; Просмотров: 759; Нарушение авторских прав?; Мы поможем в написании вашей работы!