
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегрирование по частям
|
|
|
|
Непосредственное интегрирование.
Основные методы интегрирования.
Свойства неопределенного интеграла
Свойство 1. 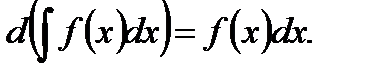
Свойство 2. 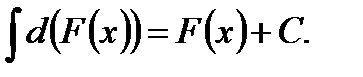
Свойство 3. 
Свойство 4. 
Свойство 5. Пусть F(x) есть первообразная для функции f(x).
Тогда 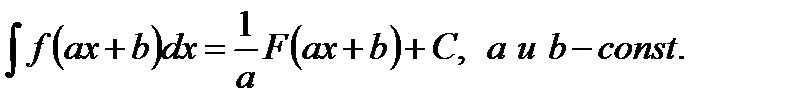
Таблица основных неопределенных интегралов
1.  2.
2. 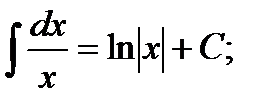 3.
3. 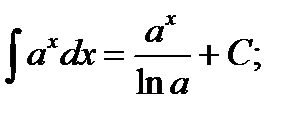
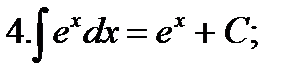 5.
5.  6.
6. 

 ;
; 
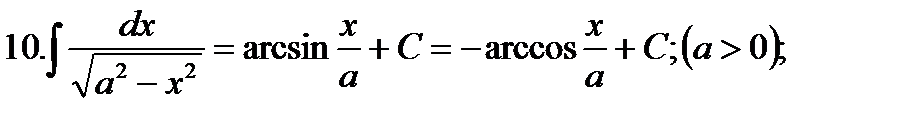
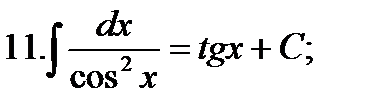 12.
12. 
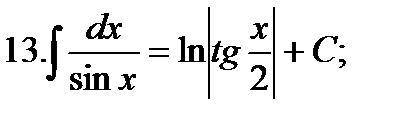

Непосредственным интегрированием называется вычисление интегралов путем использования таблицы основных неопределенных интегралов, их свойств, а также тождественных преобразований подынтегрального выражения.
Пример1. Найти неопределенный интеграл 
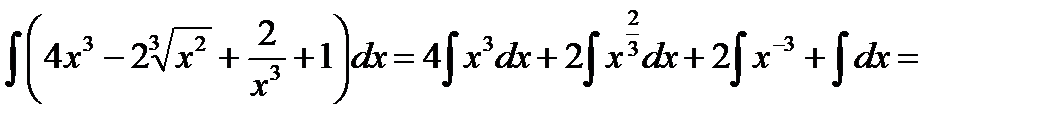
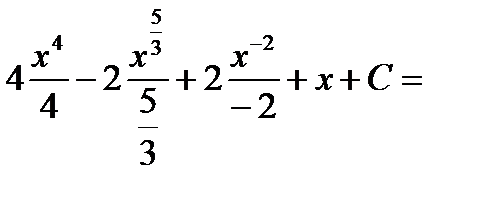

Пример 2. Найти 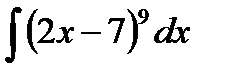 . Это интеграл вида
. Это интеграл вида 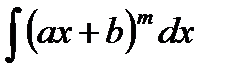 . По свойству 5 неопределенных интегралов имеем
. По свойству 5 неопределенных интегралов имеем

Теорема. Если функции u(x) и v(x) дифференцируемы на интервале (а,b), то  .
.
Таким образом, вычисление 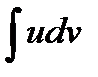 сводится к вычислению
сводится к вычислению 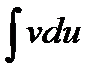 , которое может оказаться более простым.
, которое может оказаться более простым.
Пример 1. Вычислить 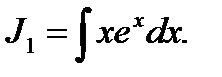 .
.
Положим u=x,  , тогда
, тогда 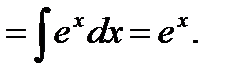 Константу С при определении функции мы опускаем, так как она входит в окончательный ответ du=dx. Отсюда по формуле (2) имеем
Константу С при определении функции мы опускаем, так как она входит в окончательный ответ du=dx. Отсюда по формуле (2) имеем 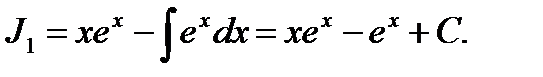
Метод интегрирования по частям применяют при вычислении следующих интегралов:
1) 
где Pn(x) – полином степени n 
В этих интегралах за u(x) принимается Pn(x) и интегрируют по частям n раз.
2 
В этих интегралах dv принимается 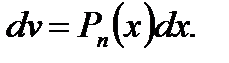
Задание 4. Решить уравнение:
4.1. С разделяющимися переменными: 
4.2. Линейное первого порядка: 
4.3. Однородное первого порядка: 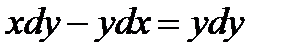
4.4. Однородное первого порядка: 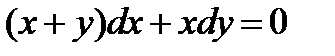
4.5. С разделяющимися переменными: 
4.6. Линейное первого порядка: 
4.7. С разделяющимися переменными: 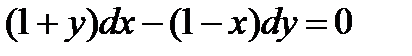
4.8. Однородное первого порядка: 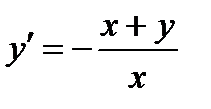
4.9. Линейное первого порядка: 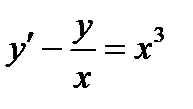
4.10. С разделяющимися переменными: 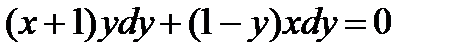
Указания к заданию 4
Дифференциальные уравнения являются одним из основных математических понятий, наиболее широко применяемых при решении практических задач. С помощью дифференциальных уравнений описывается динамика объектов или систем объектов.
|
|
|
Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции (или нескольких функций). Вместо производных в уравнение могут входить дифференциалы. Если неизвестные функции, входящие в дифференциальное уравнение, зависят только от одного аргумента, то дифференциальное уравнение называется обыкновенным дифференциальным уравнением.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Решением дифференциального уравнения n -ого порядка называется функция у (х), непрерывная на некотором интервале (а,b) вместе со своими производными до (n- 1) порядка включительно и имеющая производную у ( n )(x), такая что подстановка функции у (х) в исходное дифференциальное уравнение обращает его в тождество.
Заметим, что процедура решения простейшего дифференциального уравнения 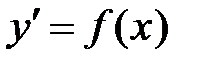 означает нахождение функции по ее производной, то есть, сводится к нахождению неопределённого интеграла
означает нахождение функции по ее производной, то есть, сводится к нахождению неопределённого интеграла 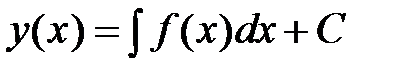 . Произвольная константа С означает, что дифференциальные уравнения имеют бесконечные множества решений.
. Произвольная константа С означает, что дифференциальные уравнения имеют бесконечные множества решений.
Уравнение в разделяющихся переменных
Процесс нахождения решения обыкновенного дифференциального уравнения называется интегрированием дифференциального уравнения.
Пример 1. Решить уравнение 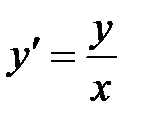 .
.
Решение. Очевидно x ≠ 0. Перепишем уравнение в виде:  и разде-
и разде-
лим переменные 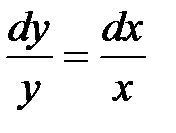 . Интегрируя обе части последнего равенства, получаем
. Интегрируя обе части последнего равенства, получаем 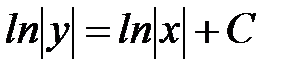 . Заменим С=lnC1, C1>0. Потенцируя полученное равенство, получаем
. Заменим С=lnC1, C1>0. Потенцируя полученное равенство, получаем
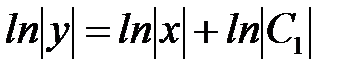 ,
,  ,
,  .
.
После раскрытия модуля получаем  . Поскольку C 1 может принимать любые значения неравные нулю, решение можно записать в виде у (x) =Сх, где произвольная постоянная С не равна нулю. Проверим потерянный при решении случай у= 0. Оно является частичным решением при C= 0 следовательно не является особым. Таким образом, общее решение исходного уравнения у (х) =Сх.
. Поскольку C 1 может принимать любые значения неравные нулю, решение можно записать в виде у (x) =Сх, где произвольная постоянная С не равна нулю. Проверим потерянный при решении случай у= 0. Оно является частичным решением при C= 0 следовательно не является особым. Таким образом, общее решение исходного уравнения у (х) =Сх.
|
|
|
|
|
|
|
|
Дата добавления: 2014-12-10; Просмотров: 441; Нарушение авторских прав?; Мы поможем в написании вашей работы!