
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исследование осесимметричной деформации многослойного основания
|
|
|
|
Пакет из конечного числа слоев, лежащий на абсолютно жестком полупространстве, назовем основанием. Каждый слой основания является однородным изотропным. Различные слои могут иметь различные толщины. В процессе деформации никакие два соседних слоя не отстают друг от друга.
В основаниях такого типа соседние слои, вообще говоря, могут проскальзывать относительно друг друга на некоторых участках контактной поверхности. При этом в различных ситуациях степень проскальзывания может изменяться от полного сцепления до идеального скольжения одного слоя по-другому. Поэтому при построении теории многослойных оснований имеет смысл рассмотреть два крайних случая – случай полного сцепления всех слоев основания и случай основания, составленного из идеально гладких слоев. Умея решать граничные задачи теории упругости для оснований со сцепленными и гладкими слоями, можно оценить решение граничной задачи для реального основания.
В этой главе ограничимся изложением теории многослойных упругих оснований с гладкими слоями.
Условимся считать нижним – слой, соприкасающийся с абсолютно жестким полупространством. Нумерацию слоев в основании будем проводить сверху вниз. Верхнему слою присвоим номер 1. Как правило, величины, относящиеся к 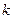 -му слою основания, будем снабжать индексом
-му слою основания, будем снабжать индексом 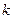 .
.
Каждый слой основания отнесем к местной цилиндрической системе координат с началом на верхней границе слоя. Начала всех систем координат расположим на одной прямой, так чтобы оси  всех местных координат совпадали с этой прямой. Для определенности считаем, что все оси
всех местных координат совпадали с этой прямой. Для определенности считаем, что все оси  местных систем направлены вниз.
местных систем направлены вниз.
Из результатов предыдущего параграфа вытекает, что для определения напряженного состояния 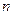 -слойного основания с гладкими слоями нужно знать
-слойного основания с гладкими слоями нужно знать 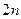 функций
функций 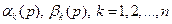 .
.
Число искомых функций можно сократить до двух, если воспользоваться предложением о том, что при деформации слои не отстают друг от друга. Из этого предложения следует, что на общей границе 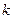 -го и
-го и 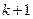 -го слоев
-го слоев
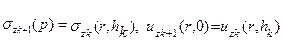 .
.
Последние соотношения выполняются при 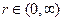 , поэтому из них получаем аналогичные соотношения между трансформантами соответствующих функций. При помощи формул (3.15) последним соотношениям придадим вид
, поэтому из них получаем аналогичные соотношения между трансформантами соответствующих функций. При помощи формул (3.15) последним соотношениям придадим вид
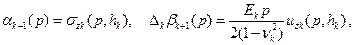 (4.1)
(4.1)
где
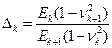 . (4.2)
. (4.2)
Если выразить теперь 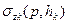 и
и 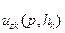 через
через  и
и 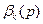 , используя результаты предыдущего параграфа, то придем к рекуррентным зависимостям между
, используя результаты предыдущего параграфа, то придем к рекуррентным зависимостям между 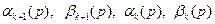 . Проведем подробно все рассуждения, связанные с получением первого соотношения. Согласно первой формуле (3.15) и формулам (3.17),
. Проведем подробно все рассуждения, связанные с получением первого соотношения. Согласно первой формуле (3.15) и формулам (3.17),
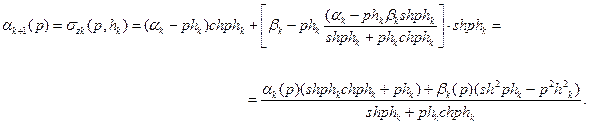
Пользуясь тем, что  , придадим первому рекуррентному соотношению окончательную форму
, придадим первому рекуррентному соотношению окончательную форму
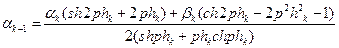 . (4.3)
. (4.3)
Аналогичным образом из второго соотношения (4.1) получим
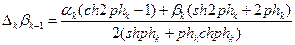 . (4.4)
. (4.4)
При помощи рекуррентных соотношений (4.3), (4.4) по известным функциям 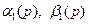 легко найти все остальные
легко найти все остальные 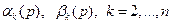 . После этого нетрудно определить трансформанты напряжений и перемещений в каждом слое основания по формулам (3.11), (3.16) предыдущего параграфа. Применив к полученным трансформантам соответствующие формулы обращения (2.2), найдем искомые напряжения и перемещения в многослойном основании.
. После этого нетрудно определить трансформанты напряжений и перемещений в каждом слое основания по формулам (3.11), (3.16) предыдущего параграфа. Применив к полученным трансформантам соответствующие формулы обращения (2.2), найдем искомые напряжения и перемещения в многослойном основании.
Здесь мы ограничимся получением наиболее простых, но важных для приложений формул для вычисления контактных нормальных напряжений между слоями и перемещений их границ. Воспользуемся тем, что по определению
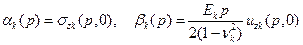 . (4.5)
. (4.5)
Считая эти функции известными, на основании формулы обращения (2.2) получаем
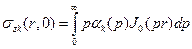 , (4.6)
, (4.6)
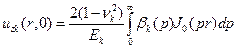 . (4.7)
. (4.7)
Подчеркнем, что из результатов этого параграфа следует важный вывод – независимо от числа слоев в основании определение его напряженного состояния сводится к отысканию лишь двух вспомогательных функций 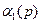 и
и  . Возникает теперь новый вопрос о том, как их найти. Нельзя указать единого способа определения функций
. Возникает теперь новый вопрос о том, как их найти. Нельзя указать единого способа определения функций 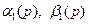 для всего многообразия граничных задач. Однако для определенных типов задач можно указать конкретные алгоритмы отыскания этих двух вспомогательных функций. В связи с этим дадим характеристику основным классам граничных задач для многослойных оснований и укажем способы отыскания функций
для всего многообразия граничных задач. Однако для определенных типов задач можно указать конкретные алгоритмы отыскания этих двух вспомогательных функций. В связи с этим дадим характеристику основным классам граничных задач для многослойных оснований и укажем способы отыскания функций 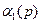 и
и  .
.
§5 Классификация граничных задач
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 429; Нарушение авторских прав?; Мы поможем в написании вашей работы!