Исследование решения контактной задачи

Если внимательно исследовать совершенные в §6 выкладки, то можно прийти к выводу, что для обоснования их достаточно установить непрерывность функции .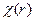

Прежде всего, докажем, что интегральное уравнение (6.7) является уравнением Фредгольма второго рода. Для этого нужно показать, что ядро и свободный член уравнения интегрируемы с квадратом соответственно в областях 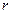, 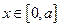и , т. е. нужно показать, что существуют интегралы от квадратов названных функций в указанных областях. Мы докажем большее – непрерывность ядра и свободного члена уравнения (6.7).

Для доказательства непрерывности ядра

достаточно показать [7], что подынтегральная функция в несобственном интеграле непрерывна относительно переменной интегрирования и параметров , и что несобственный интеграл сходится равномерно относительно и 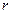в указанной области.

По первому свойству функций податливости является непрерывной функцией, функции и 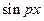непрерывны относительно . Поэтому подынтегральная функция в несобственном интеграле непрерывна по всем переменным, причем область изменения переменных и 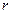может быть любой. Равномерная сходимость интеграла легко устанавливается при помощи признака Вейерштрасса.

В самом деле

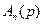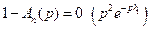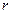и сходится, так как по третьему свойству функции при .Таким образом, ядро интегрального уравнения (6.7) непрерывно для любых и .

Перейдем к исследованию свободного члена уравнения (6.7)

.

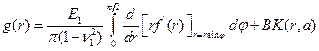Непрерывность его в области вытекает из доказанной непрерывности ядра по обоим переменным и ограничения наложенного на поверхность штампа – функция непрерывна в . В силу этого ограничения, подынтегральная функция в (7.1) непрерывна по обеим переменным в области . Поэтому первое слагаемое в выражении непрерывно в промежутке [1].

Известно [7], что решение интегрального уравнения (если оно существует), у которого ядро и свободный член непрерывны, является непрерывной функцией. В связи с этим, для доказательства непрерывности функции 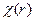нужно выяснить, при каких условиях уравнение (6.7) имеет решение. Известно [7], что интегральное уравнение

всегда разрешимо, если 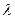не является характеристическим числом ядра .

Множество характеристических чисел четно и не имеет предельной точки на конечном расстоянии от начала координат в комплексной плоскости. Ни одно из характеристических чисел не равно нулю. Для рассматриваемого интегрального уравнения (6.7) . Поэтому при 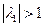решение уравнения (6.7) существует и по сказанному выше будет непрерывной функцией в .

Наименьшее по модулю характеристическое число 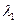ядра допускает следующую оценку снизу:

,

где

.

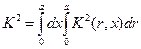Так как , то и поэтому .

Требуя теперь, чтобы

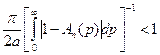, (7.1)

будем иметь 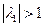. Таким образом, при выполнении условия интегральное уравнение (6.7) разрешимо, и его решение является непрерывной функцией.

Исследуем теперь поведение контактных напряжений в окрестности границы площадки контакта, т.е. при . Рассмотрим второе слагаемое в формуле (6.9). По доказанному, функция 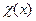непрерывна в промежутке , а – знакопостоянная функция на промежутке интегрирования . Поэтому на основании обобщенной теоремы о среднем [1]

.

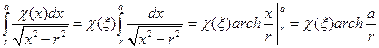Здесь 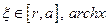– функция обратная 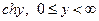(название функции 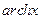– ареакосинус). Функция 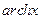непрерывна в области .

При очевидно и , поэтому, в силу ограниченности непрерывной функции 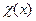в замкнутом промежутке , приходим к выводу, что второе слагаемое в формуле (6.9) стремится к нулю. Поведение первого слагаемого зависит от значения пока что неопределенной константы . Если , то 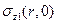, 0 при . Этот случай соответствует неполному погружению штампа в основание. В случае 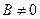при . Это возможно при 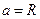и соответствует полному погружению штампа в основание. В обоих случаях в формуле (6.9) имеется по одной неопределенной величине. При неполном погружении , но неизвестен радиус площадки контакта. При полном погружении 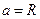, но неизвестно значение величины . Для определения этих неизвестных величин служит условие (6.10).

В качестве примера, получим решение задачи о вдавливании выпуклого штампа в упругое полупространство. Для упругого полупространства функция податливости 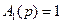. Поэтому, согласно формуле (6.8), 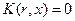. Стало быть, на основании формулы (6.7),

.

Подстановка этой функции в формулы (6.9), (6.10) приводит к искомому решению.

В частности, для штампа с плоским основанием функция , поэтому

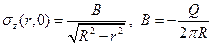
Окончательная формула для контактных напряжений имеет вид

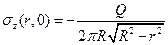
где 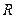– радиус основания штампа, – сила, вдавливающая штамп с плоской подошвой в упругое полупространство.

Дата добавления: 2014-11-29