Некоторые сведения о функциях Бесселя первого рода

ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ МНОГОСЛОЙНОГО ОСНОВАНИЯ

Необходимой предпосылкой для изучения свойств функций Бесселя и многих других специальных функций является знание свойств гамма-функции Эйлера .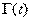

Для значений

. (1.1)

При интеграл расходится, и значения функции 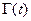для таких необходимо определять другим способом.

Нетрудно убедиться в том, что подынтегральная функция в (1.1) и любые её производные по параметру непрерывны в области 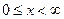, и интегралы от этих функций (по ) равномерно сходятся относительно параметра . Отсюда следует:

Свойство (1.1) Гамма-функция 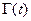– непрерывна и любое число раз дифференцируема по для значений .

Интегрированием по частям получаем

.

Свойство (1.2)

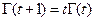. (1.2)

Из формулы (1.1) при находим . Поэтому на основании свойства (1.2) 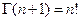, если 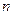натуральное число .

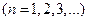Свойство 2 можно использовать для того, чтобы определить функцию 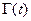для . С этой целью напишем формулу (1.2) по иному

. (1.3)

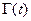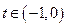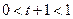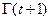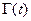Теперь легко естественным образом определить значения для . В самом деле, если , то , и может быть вычислена по формуле (1.1). Естественно считать, что в промежутке гамма-функция принимает те значения, которые получаются по формуле (1.3).

Построив функцию 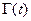в промежутке , при помощи (1.3) определим её в промежутке . Этот процесс можно продолжить далее и установить, какие значения принимает 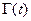при любых , кроме .

Таким образом, при помощи формул (1.1) и (1.3) гамма-функция 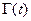может быть определена при любых действительных кроме 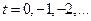. Эти точки, как это следует из (1.3), являются простыми полюсами функции 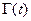. Вследствие этого

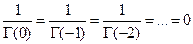. (1.4)

Из сказанного выше относительно функции 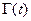следует, что её график имеет вид

Рисунок 1.1 – График гамма-функции

Приведем без доказательства еще два свойства, которые имеют место для любых из области определения гамма-функции.

Свойство (1.3)

.

В частности, при из свойства (1.3) следует, что

.

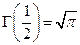Свойство (1.4)

.

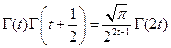Заметим, что свойства (1.2) – (1.4) в совокупности вполне характеризуют функцию 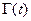, т.е. любая функция, обладающая этими свойствами, совпадает с .

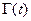Перейдем теперь к изучению свойств функций Бесселя первого рода. Функция Бесселя 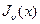может быть определена рядом

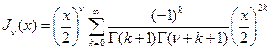. (1.5)

Здесь – аргумент функции, – называют индексом, порядком, значком. Величины считаем в дальнейшем действительными.

Наиболее просто область сходимости ряда установить на основании признака д’Аламбера. Для этого вычислим, используя свойство (1.2) гамма-функции, предел

.

Следовательно, данный ряд сходится абсолютно при любом , а это означает, что его радиус сходимости 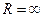. Напомним, что степенной ряд в круге сходимости можно почленно дифференцировать любое число раз.

Функция 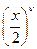при действительном определена в интервале 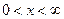и дифференцируема в нем любое число раз. Поэтому функция Бесселя 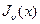имеет область определения , и в этой области имеет непрерывные производные любого порядка.

Если индекс целый , то формула (1.5) определяет функцию 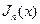в области 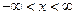, при этом

. (1.6)

Докажем это утверждение, считая 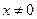и . Согласно формуле (1.5)

.

Но так как на основании (1.4)

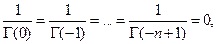
то все слагаемые первой суммы в квадратных скобках равны нулю, поэтому

= .

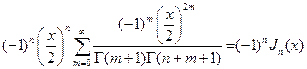Из полученного результата следует, что точка является, устранимой особой точкой функции . В дальнейшем считаем 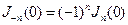. В силу этого формула (1.6) становится справедливой для всех .

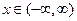Приведем без доказательства ряд фактов из теории функций Бесселя, которые нам потребуются в дальнейшем.

Функция 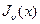является частным решением дифференциального уравнения

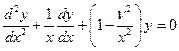, (1.7)

которое называется уравнением Бесселя.

Функции связаны рекуррентными соотношениями

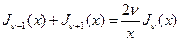, (1.8)

. (1.9)

Полезно для дальнейшего еще одно соотношение подобного типа

, (1.10)

которое является следствием двух предыдущих.

В справедливости формул (1.7) – (1.10) можно убедиться непосредственной подстановкой в них соответствующих рядов (1.5).

При поведение функций Бесселя 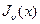характеризует асимптотическая формула

.

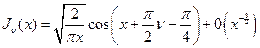При использовании функций Бесселя на практике не всегда удобно пользоваться степенными рядами для этих функций. Полезно иметь и другие представления, например, интегральные. Получим необходимые для дальнейшего интегральные представления функций Бесселя с целым индексом. Для этого нам потребуется производящая функция для таких функций, т.е. такая функция , что

.

Попытаемся найти её. Для этого обратимся к рекуррентному соотношению (1.8)

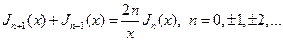
Умножим обе части равенства на 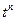и затем просуммируем по всем 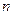. Получим

или

.

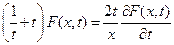Определяя из этого уравнения , получим

, (1.12)

где 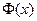– произвольная функция .

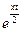Разлагая в ряды по степеням функции и , и затем, перемножая их, убедимся, что коэффициентами степенного ряда по функций будут функции . Таким образом, в получившемся выражении (1.12) для производящей функции следует взять 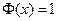. Итак, искомая производящая функция имеет вид

.

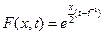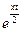При разложении этой функции в ряд Лорана в окрестности точки приходится раскладывать в аналогичные ряды функции и . Ряд для первой функции имеет область сходимости 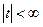, а ряд для второй 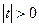. Причем оба ряда будут сходиться и для комплексных значений . Поэтому, полагая в выражении производящей функции и используя формулу (1.6), получим

.

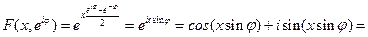
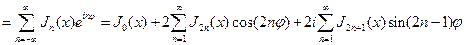Отсюда следует, что

,

.

Эти разложения в ряды Фурье функци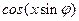й и носят имя Якоби.

Из курса анализа известно, что каждая из систем функций 1, и ортогональна на отрезке 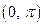. При этом

Поэтому из разложений Якоби получаем искомые интегральные представления для функций Бесселя целого порядка

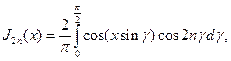(1.13)

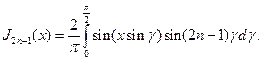
Покажем теперь, что функция обладает следующими интересными свойствами

(1.14)

(1.15)

Рассмотрим вспомогательный интеграл

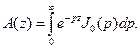
Этот интеграл сходится равномерно относительно в области , где – любое положительное число. Мажорантой подынтегральной функции является . (В самом деле, из (1.13) вытекает, что 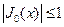, поэтому 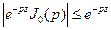. Так как 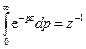– сходится, то – мажоранта).

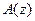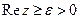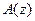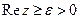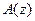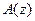Если разрешить принимать комплексные значения, то интеграл будет равномерно сходиться в области . Так как подынтегральная функция в непрерывна в области , то представляет собой непрерывную функцию [1] в области . Вычислим интеграл , опираясь на представление (1.13) и считая 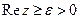. Имеем

.

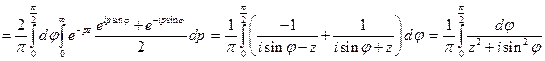В последнем интеграле сделаем замену переменной . Тогда

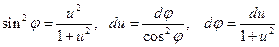
и

Здесь в области выбирается та ветвь многозначной функции , которая для действительных принимает положительные значения.

Таким образом, в области

. (1.16)

Этим показано, что две аналитические функции комплексной переменной и совпадают в области . Отсюда следует, что совпадают и предельные значения этих функций в тех точках границы области , которые не являются особыми точками функции . Следовательно, при ( – действительное число)

.

Очевидно, что

.

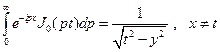Если воспользоваться формулой Эйлера и разделить действительную и мнимую части правой и левой частей последнего равенства, получим (1.14), (1.15).

Дата добавления: 2014-11-29